基于改进RRT的关节机械臂路径规划*
张婷婷,柳林燕,汪惠芬
(南京理工大学机械工程学院,南京 210094)
0 引言
关节机械臂是目前工业场景中应用最广泛的工业机械臂种类之一,其中6自由度机械臂的应用率最高,例如喷漆,装配等工作。因为6自由度的机械臂具有:第一,基本可以到达满足工作空间的所有点;第二,可以通过控制连续实现复杂的运动。因此需要对关节机械臂进行路径规划,使其更好地完成指定任务。
机械臂的路径规划即从起始点开始朝着目标点运动,躲避整个空间中出现的障碍物,并且最终找到一个最优或者相对优化的路径。目前已有A*,RRT,随机路标图(probabilistic roadmap method,PRM)等成熟的算法。
传统的RRT算法,虽然概率完备但是每次试验得出的路径并不是最优的,并且有很多的冗余点。基于此类问题,孙丰财等[1]加入了偏向策略,实现了时间优化,但是其在三维空间中的路径优化并不明显。在此之后,提出一种渐进最优性(距离最短)的RRT*算法[2-3],该算法在RRT的算法上比对多个父节点,找到实现每个随机点路径的最短距离,最后实现最终路径最短并且可以实现更高的搜索成功率,但RRT*有每次搜索时相似度不高,路径结果差异较大等缺点。Informed-RRT*算法采用的是先验知识的改进操作,即先利用RRT*算法找到第一条路径的前提下,对该路径进行优化[4-5],但是因为基于的RRT*采样就是随机的,无法保证首次的路径就是最优的,会导致对此条路径做优化,无法得到最优解。上述算法在二维空间中已有详细的验证,但在三维空间中会出现并不理想的结果。
本文基于三维空间的复杂条件下,针对传统的RRT算法,进行目标导向处理使得随机树更趋向于目标点,再进行冗余检测剔除多余的节点,对处理后的随机树进行平滑处理,更加符合六自由度机械臂的空间运动。
1 算法基础
1.1 机械臂运动学建模
本文采用的是某品牌型号为ER10-900的机械臂,工作空间是900 mm。建立机械臂的数学模型采用的是D-H参数,此方法需要在机器人的每个连杆的关节轴处建立一个笛卡尔坐标系,机械臂的DH连杆坐标系如图1所示。建立运动学模型,是为了在得出路径后,通过运动学逆解法,让机械臂沿着该路径进行运动,在本文的后续会有展示。

图1 机械臂的DH连杆坐标 图2 机械臂的模型
所用的4个参数代表的意义分别是:θi是关节角,di是连杆偏移量,ai是连杆长度,αi是连杆的扭转角。根据以上的4个参数可以表述相邻俩连杆之间的空间状态,然后依据机械臂的逆运动学,可以将路径规划中所得到的每个点在笛卡尔坐标系中的表示形式,转化为在关节空间中每个连杆需要的变化[6]。依据上述理论,在MATLAB中模拟出本文所用机械臂的模型如图2所示,此状态为机械臂最灵活的空间状态,所以最终运动完都回到此状态。
1.2 机械臂碰撞检测
机械臂碰撞检测是进行路径规划的前提条件,主要分为机械臂各连杆与工作空间障碍物的碰撞检测和机械臂自身杆件的碰撞检测。本文所基于的背景条件,只需进行障碍物和机械臂杆件的碰撞检测。因为实际环境中的障碍物形状各异,为了避免不必要的计算时间,文献[7]以长方体包络检测法,而本文使用的是球体包络检测[8]。
机械臂以不同半径的圆柱体表示不同连杆,通过检测圆柱体的轴线和障碍物球体之间的距离,来判断两者是否发生碰撞。
2 RRT算法原理
RRT算法与PRM算法较为类似,都是一种概率完备型算法,是通过在已知的地图上产生抽样点并建立无向图,进而通过搜索的方法寻找到相对最优路径。不同点在于,PRM算法在一开始就通过抽样在地图上构建出完整的无向图,再进行图搜索;而RRT算法则是从某个点出发一边搜索,一边抽样建图[9]。但是如果规划器的参数设置不合理(如搜索次数太少、采样点过少等),都可能使RRT算法最终无法找到解,因此参数设置对于RRT算法来说,是至关重要的。
以xstart为起始点,xgoal为目标点,建立搜索树T,其运动过程如下:
(1)首先产生第一个节点xstart属于xfree,在每一次循环中,产生一个随机点xrand,随机点的生成是任意的,即可以在整个状态空间X内;
(2)在产生随机点后,遍历随机树中的每一个节点,计算每一个节点与该循环生成的随机点之间的距离,找出距离此随机点最近的节点,记为xnearest;
(3)定义一个固定步长stepsize,当找到xnearest时,向xnearest与xrand连线方向扩展stepsize长度,扩展后产生新的节点xnew;
(4)在插入新节点xnew的过程中,如果xnearest、xnew和xnearest到xnew之间的边任意一个位于障碍物空间xobs中或者与xobs相交,则此次循环不添加任何节点,在下一次循环中重新生成新的随机点xnew,然后再进行判断,如果属于xfree,则保留新节点;
(5)重复上述步骤直至xnew和xgoal小于一个固定的阈值,则代表到达目标点,算法终止。
根据上面的基本原理,得出传统的RRT算法存在随机性大,具有盲目性,因此导致从起始点到目标点扩展的时间较长,并且在本文设定的迭代次数为10 000内寻找的成功率不高;冗余点较多,增加了路径成本;路径抖动较大,对于本文所述的6自由度机械臂运动而言,并不友好,为了改善以上缺点,需要对RRT算法进行改进。
3 改进的RRT算法
3.1 目标导向处理(M-RRT)
本文采用的是向目标点进行扩展,将原来随机扩展的节点,再处理后使其更有方向性的运动[1,7,10-12]。在随机函数的前提下引入系数,沿着xnearest到xrand和xnearest到xgoal两个方向分别取u1、u2两个系数,在这两个系数的共同作用下产生全新的节点,新节点的产生如式(1)所示。
(1)
主要步骤如下:
(1)在三维位形空间中生成xstart、xgoal和障碍物模型;
(2)起始点在位形空间中每次随机采样2个点,按照距离目标点的远近排序,将最近的节点设定为xnearest,与xgoal进行连线,然后对该线段进行障碍物碰撞检测,当发生碰撞时u2=0,随机树朝着产生新随机点的方向扩展;不发生碰撞时u1=0,随机树朝着目标点的方向扩展;
(3)当xgoal与新生成的xnew的距离小于或等于设置的固定步长时,则xnew=xgoal。
目标偏向采用的是两种不同的步长,即引入的参数u1=10和u2=15,当随机树偏向目标点扩展时,所用的步长较大;当随机树偏向新产生的随机点扩展时,所用的步长较小。因为朝着目标点扩展是已经确定该新节点是正确的方向,所以可以给予一个大的步长加快运算;朝着新的随机点的运动,因为无法确定下一次检测是否是正确的方向,所以要用小步长来进行扩展。
3.2 冗余检测处理(R-RRT)
改进的算法引入系数后,明显的降低了随机性,随机树大概率朝着目标点进行运动。虽然在上述的改进下时间缩短了很多,但是路径长度的变化并不大,本文想要的是在时间变化较小的前提下,路径相对较短[13-16]。
基于上述的改进,对产生随机树的每个节点进行冗余检测,冗余检测示意图如图3所示。
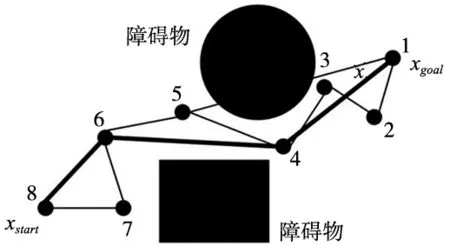
图3 冗余检测示意图
具体的操作步骤如下:
(1)以目标点为冗余检测的开始点,下一个节点为新的目标点;
(2)用线段连接这两个点,将线段进行n等分划分,再依次判断等分点是否在障碍物内;
(3)若有等分点在障碍物内,则将该新的目标点的子节点放入优化后的随机树的节点中;若等分点不在障碍内,则对该节点的父节点进行冗余检测;
(4)直到将冗余检测起始点到新的目标点之间的所有冗余点删除后,再以此时优化后的随机树中的目标点为开始点,进行后续的冗余检测;
(5)将所有节点冗余检测完后,生成一个节点更少的随机树。
由图3可知基于目标导向后的路径是8-7-6-5-4-3-2-1,再通过冗余检测后的路径为8-6-4-1,理论上大大地缩短了路径长度。
3.3 路径平滑处理(P-RRT)
经过优化后的路径,虽然非必要的转折点变少,但是相邻节点之间的拐角变大,机械臂在依据此路径运动时,会引起机械臂的冲击和振动[12]。为了减少机械臂后续可能发生的磨损和破坏,本文采用的是基于B样条曲线的平滑处理。
贝塞尔曲线是采用递归的方法来绘制曲线,从而逼向特征多边形,这意味着若修改一个控制节点,则整个曲线都会发生变化,并且幂次过高则会更难修改等问题。因此基于这些问题,RYBUS等[16-17]提出了B样条曲线,即用B样条曲线的基函数来代替贝塞尔函数的基函数。B样条曲线可以指定阶数,还可以在移动控制点的前提下,只改变部分曲线的形状,而不会对整体发生大改变。即B样条采用的是将一条曲线变成多段贝塞尔曲线的拼接。设现有n+1个控制点Pi,则k阶(k-1)次B样条曲线的表达式为:

(2)
式中,Ni,k(t)是B样条曲线函数的基函数。
B样条曲线基函数是以一个非递减的参数为t的序列所决定的k阶分段多项式,则基函数Ni,k(t)可用deBoor-Cox的递推公式表示为:
k=1时,
(3)
k>1时,
(4)
Ni,k(t)是由k-1阶B样条基函数递推得出,t下标的范围是i到i+k。即要定义第i个k阶B样条Ni,k(t),需要用到k+1个节点ti...tk,即[ti,ti+k]这个区间是Ni,k(t)的支撑区间。(支撑区间是指函数值不为0的区间)。
为了保证生成的曲线分别与第一个和最后一个控制点的第一条边和最后一条边相切,则第一个节点和最后一个节点的重复度必须为k。针对冗余检测后的路径,进行平滑处理,得出的路径为8-6′-4′-1,二维路径B样条曲线示例如图4所示。
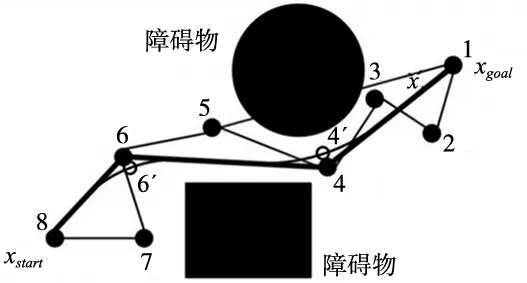
图4 二维路径B样条曲线示例图
4 仿真实验
根据上述改进的理论,在MATLAB中进行实验仿真,为了更好的验证上述改进算法,障碍物选取较为简单的球体包络,并且相对集中的分布在起始点与目标点的对角连线周围,起始点为(10,10,10),目标点为(150,150,150),有效随机树用红色线条表示。最终仿真出来的算法路径对比图如图5所示,未经任何修改的传统RRT如图5a所示,增加系数进行目标导向处理后M-RRT如图5b所示,基于目标导向后进行冗余检测和平滑处理后的R-RRT和P-RRT如图5c所示。

(a) 传统RRT (b) M-RRT
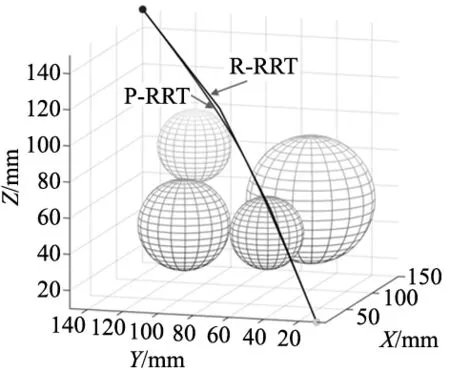
(c) R-RRT和P-RRT图5 算法路径对比图
可以看出,未经过处理的传统RRT在产生随机树的情况下,出现了较多的分叉树,这不仅会增加迭代的次数,导致时间变长,同时也会使得产生的节点数变多,最终路径变长。
在通过目标导向处理引入参数u1和u2后,随机树中出现的分支条少了很多,产生的随机点更多的是朝向目标点及进行随机树的扩展。基于目标导向后的路径进行冗余检测,从图中可以明显看出路径的节点变的更少,路径变得更适宜6自由度机械臂的运动。以第1节为基础建立的机械臂运动学模型,经过相关的正逆运动学计算[18],运动路径示意图如图6所示。
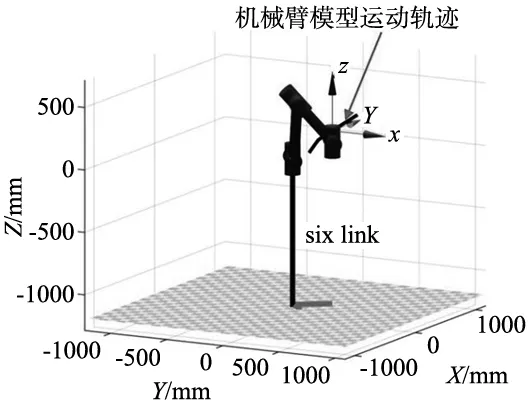
图6 机械臂模型的运动路径示意图
本文所给的搜索次数是10 000,进行30组仿真模拟,RRT算法出现一次无法找到路径的情况,而M-RRT和R-RRT则是每次都成功找到路径。根据数据绘出时间和距离对比如图7所示。
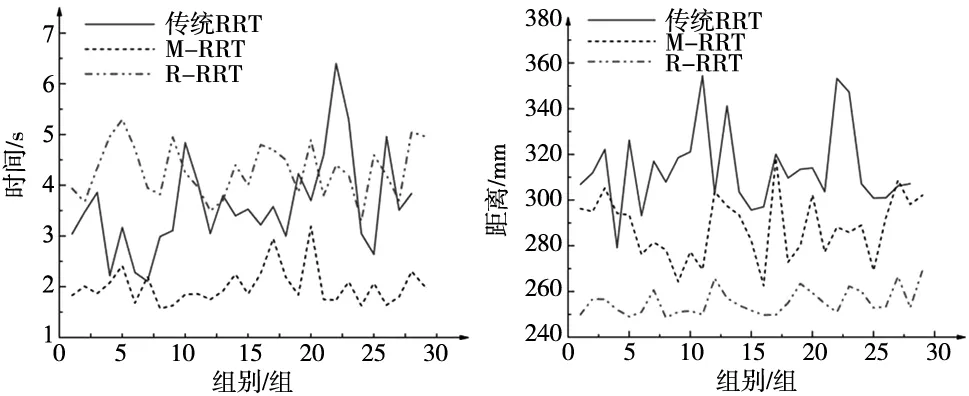
(a) 时间对比图 (b) 距离对比图图7 时间和距离对比图
可以看出,M-RRT的时间整体优于传统RRT,但是在路径长度方面并没有发生较大的变化,因此在此基础上进行冗余检测,得出R-RRT缩短路径长度。
本文所研究的机械臂路径规划对于路径长度更为侧重,因此R-RRT算法虽然平均时间相较于传统RRT多出0.6 s,但是平均路径长度缩短了58 mm。R-RRT的时间增加的原因是在进行冗余点检测时,三维空间各等分点的检测迭代次数较多。后续相关研究中,如果侧重于时间可以仅用目标导向处理的M-RRT,如果侧重路径长度则可以使用本文最终改进R-RRT的算法处理。P-RRT则是对最终路径用B样条曲线进行平滑处理,对路径长度和总体时间影响较小,故不进行相关对比。算法比较结果如表1所示。

表1 算法比较结果
5 总结
本文针对其他学者基于RRT算法做出的改进中的不足,以三维空间关节机械臂为研究基础,对传统RRT算法做出改进。首先建立关节机械臂的运动模型,模拟相关障碍物进行路径规划,再通过仿真让机械臂以此路径运动,最终得到结论如下:
(1)本文的M-RRT可以有效地引导随机树朝着目标运动,运动时间有比较明显的缩短;
(2)R-RRT最终处理后的路径有相应的缩短,但是提升相对M-RRT来说较小;
(3)利用B样条曲线对缩短后路径进行平滑处理,更好地符合6自由度机械臂的运动。

