突出真实情境 聚焦数学推理

段素芬

摘  要：PISA2022以数学为主要测评领域，数学素养直面21世纪技能. 基于PISA2022数学素养测评示例的视角，参照情境、内容、过程三個维度，于真实情境中聚焦数学推理核心能力. PISA2022为了迎接未来的挑战和发展的理念和追求始终不变，同时也在与时俱进地思变. 审视我国数学学业测评试题的编制，建言应重视真实情境的试题构建，突出问题解决的试题主旨，加强数学推理的试题思维.

关键词：PISA2022;数学素养;示例;真实情境;数学推理

PISA（Program for International Student Assessment，简称PISA）是由经济合作与发展组织（The Organization for Economic Cooperation and Development，简称OECD）实施的每三年一轮的国际评估项目. 数学作为主要测评领域经历了PISA2003，PISA2012，即将到来的是PISA2022. 立足于PISA2022数学素养，以试题为切入点分析PISA2022的示例特征，对我国数学学业试题编制有很大的启示.

一、PISA2022数学素养之“隅”

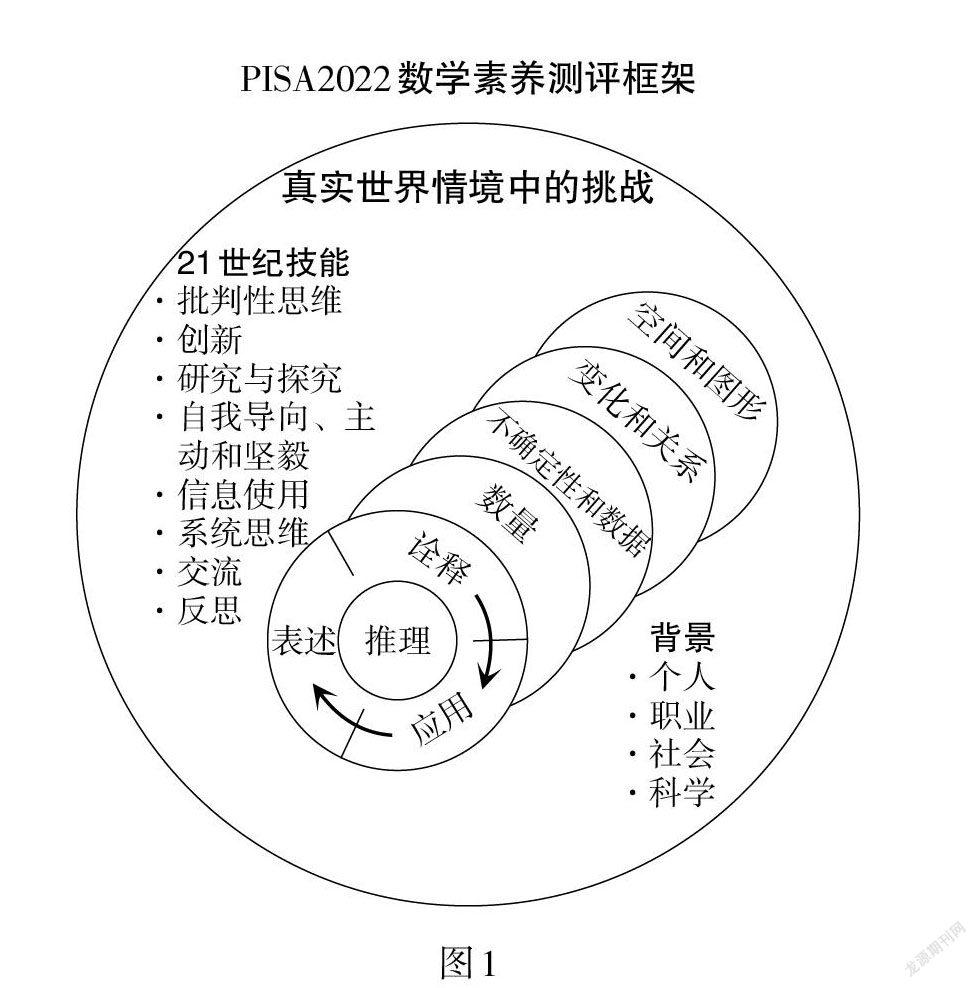
PISA2022数学素养是指个体在真实世界的不同情境中进行数学推理，并表达、应用和阐释数学解决问题的能力. 由PISA2022数学素养测评框架（如图1）可以看出：数学推理是轴心，数学情境是背景，数学内容是载体，数学问题是指向. 突出数学推理的核心地位，强调数学情境的真实世界，重视数学内容的知识领域，关注数学问题的实际解决. 同时，PISA2022关注到世界范围对于21世纪的知识及技能在教育中的增长，关注到教育和技能的未来.

1. 数学情境之“真”

关注现实与面向未来是PISA数学素养观的基调. PISA测试一以贯之地重视现实世界的真实情境，关注现实世界的数学化，强调数学内容与真实情境的关联，将对数学的理解置于现实世界的真实情境中，强调学生在具体情境中运用数学解决问题的能力. PISA2022依然延续情境的四种类型——个人情境、职业情境、社会情境、科学情境，并更加清晰地展现如下性质：第一，全面性，即基本上涵盖了学生应对真实世界的问题;第二，层次性，即首先是最贴近学生的个人生活情境，其次是学生即将面对的职业情境，然后是学生日常生活中遇到的社会情境，最后是距离学生最远的科学情境;第三，不连贯性，即信息技术的突飞猛进与大数据时代的迅速发展都对学生的真实世界构成了巨大影响，时代发展的跳跃性决定了现实世界真实情境的不连贯性.

2. 数学推理之“重”

从数学本质来讲，任何数学问题都离不开数学推理. 数学推理（mathematical reasoning）是数学素养的核心，贯穿于解决问题的整个过程. 从实际问题中抽象数学问题，在解决问题中选择数学方法，于诠释问题中凝练数学表达，无一例外都涉及数学推理. 数学推理作为PISA2022数学素养的第一要素，具有深刻的内涵和意义，包括六大核心要素：（1）理解数字系统及其代数性质;（2）领会数学抽象与符号表征的意义;（3）理解数学结构及其规律;（4）识别数量之间的函数关系;（5）使用数学模型理解现实世界;（6）理解变化是统计学的核心. PISA2022将数学推理与问题解决的三个过程（数学表述、数学应用、数学诠释）联系在一起，凸显数学推理的核心位置，目的是通过数学推理驱动“表述、应用、诠释”，以反映数学问题的解决过程. PISA2022通过问题解决对学生的数学推理提出具体、明确的要求. 例如，在问题解决的“表述”维度中要求学生“在一个模型中识别关键变量”;在问题解决的“应用”维度中要求学生“计算新的表达式的结果”;在问题解决的“诠释”维度中要求学生“做出简单总结”或“给出合理的理由”等.

二、PISA2022数学示例之“貌”

PISA2022数学示例，可以帮助解释数学素养测评框架. PISA2022将完全采用基于计算机的数学测评，所有测试题都将在计算机端呈现. 这种方式更加契合21世纪公民信息素养的诉求，同时更为生动、丰富、动态，更贴近真实世界的情境，得以在计算机上实现模拟仿真.

1. 四个示例

案例1：智能手机的使用.

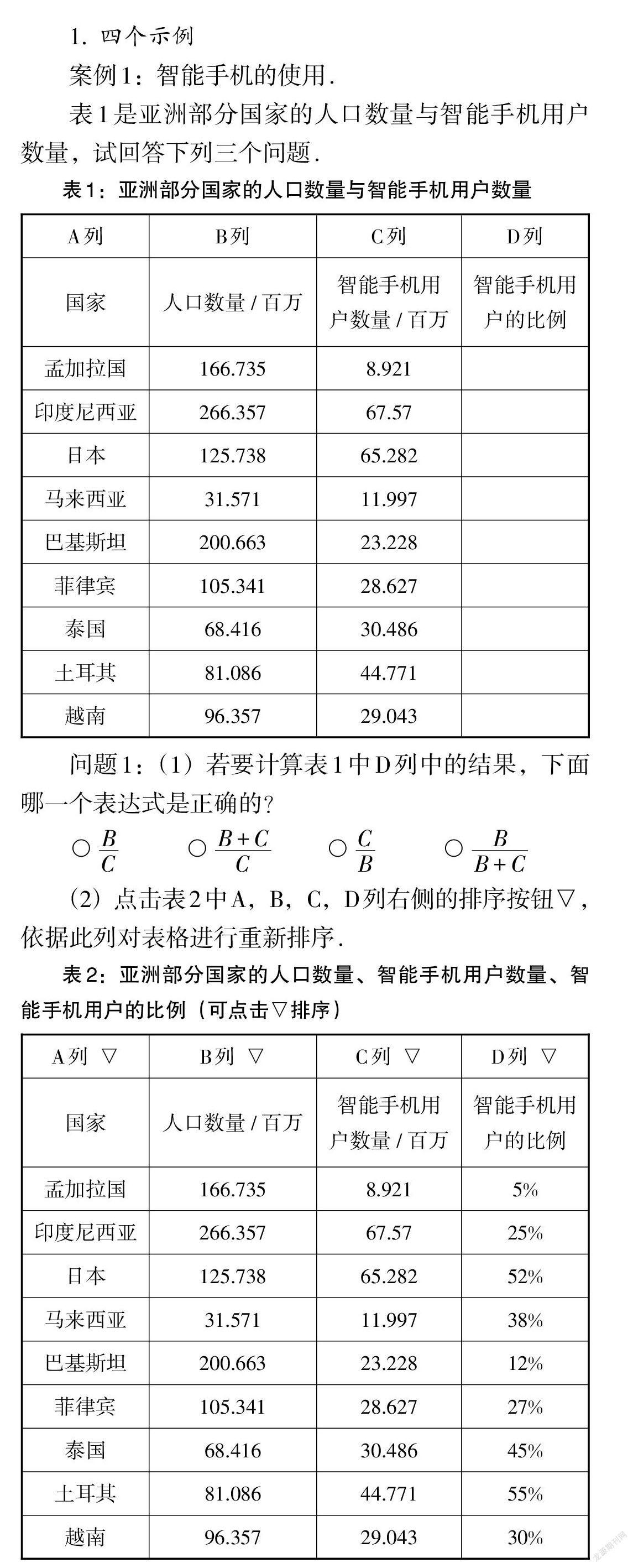
表1是亚洲部分国家的人口数量与智能手机用户数量，试回答下列三个问题.

问题1：（1）若要计算表1中D列中的结果，下面哪一个表达式是正确的？

○[BC]     ○[B+CC]    ○[CB]     ○[BB+C]

（2）点击表2中A，B，C，D列右侧的排序按钮▽，依据此列对表格进行重新排序.

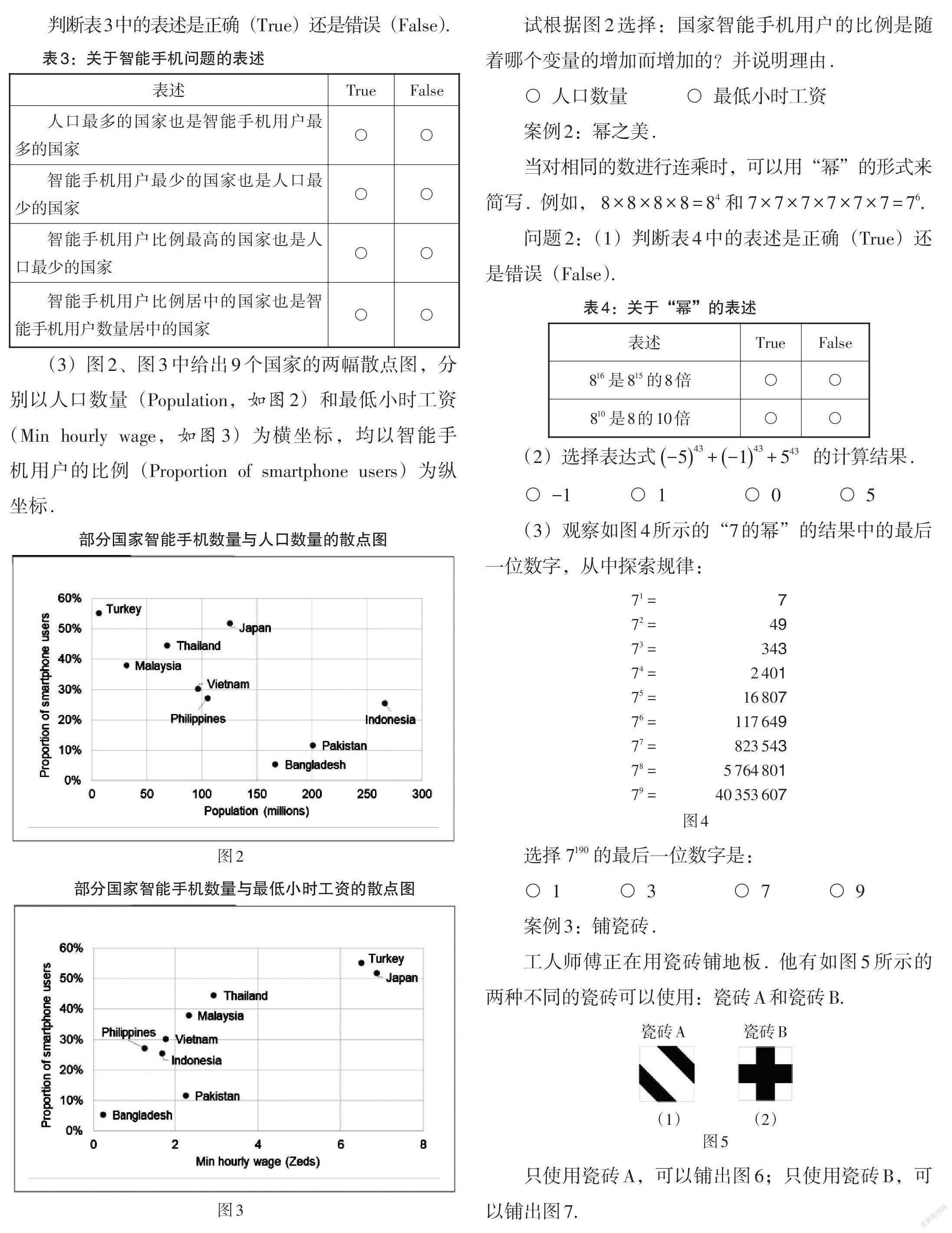
判断表3中的表述是正确（True）还是错误（False）.

（3）图2、图3中给出9个国家的两幅散点图，分别以人口数量（Population，如图2）和最低小时工资（Min hourly wage，如图3）为横坐标，均以智能手机用户的比例（Proportion of smartphone users）为纵坐标.

试根据图2选择：国家智能手机用户的比例是随着哪个变量的增加而增加的？并说明理由.

○ 人口数量      ○ 最低小时工资

案例2：幂之美.

当对相同的数进行连乘时，可以用“幂”的形式来简写. 例如，[8×8×8×8=84]和[7×7×7×7×7×7=76.]

问题2：（1）判断表4中的表述是正确（True）还是错误（False）.

（2）选择表达式[-543+-143+543] 的计算结果.80253BB6-C083-4B3F-B36D-B6DC0592CF56

○ -1      ○ 1        ○ 0      ○ 5

（3）观察如图4所示的“7的幂”的结果中的最后一位数字，从中探索规律：

选择[7190]的最后一位数字是：

○ 1      ○ 3        ○ 7      ○ 9

案例3：铺瓷砖.

工人师傅正在用瓷砖铺地板. 他有如图5所示的两种不同的瓷砖可以使用：瓷砖A和瓷砖B.

只使用瓷砖A，可以铺出图6;只使用瓷砖B，可以铺出图7.

参考图8的图案. 使用鼠标来拖放瓷砖A或瓷砖B，并完成下列问题.

问题3：（1）图8的图案是使用两种类型的瓷砖组合创建的. 试继续以同样的方式来铺地板，使用鼠标拖放瓷砖到合适的位置来完成地板的其他部分.

（2）工人师傅想给图8的方案做一套铺磚指令. 试将下面的几个词语拖放到相应的空格处，以完成可以生成图8的指令.

[如果] [那么] [否则] [瓷砖A] [瓷砖B]

铺砖指令：

若行 = 1至4，

则从左手边第一块砖开始铺：

如果行是奇数行，

那么第一块砖铺   ，

否则第一块砖铺   ;

然后继续往右铺：

如果左面的是   ，

接着靠右铺   ，

就铺   .

接下来继续铺.

（3）参考图9的“平铺图案”，点击选项回答下列问题.

工人师傅希望能够预测在网格上的任何位置是哪种瓷砖. 例如，他想知道在标记的位置（m，n）上是哪一种类型的瓷砖. 观察图9的规律，特别是用边框标出的4块瓷砖，从表5的选项中选择正确的规则，以预测网格位置为（m，n）的瓷砖类型.

（4）另一种描述图案规律的方法是在相应的网格位置上写出与每块瓷砖对应的字母. 用字母来记录如图10所示的瓷砖的图案，如图11所示.

图13是使用如图12所示的B和C两种瓷砖组合创建的.

观察图13的铺设规律. 图13、图14中用边框标出的部分是对应一致的. 试在图14的网格中用字母B或字母C来记录用边框标出的部分内的每个位置的瓷砖类型.

（5）图15是某种图案中的一部分，这个区域是由如图16所示的三种瓷砖组合创建的：瓷砖A、瓷砖B和瓷砖C.

表6中哪个字母表示正确描述了图15中图案的一个3 × 3的瓷砖单元？

案例4：购买决策.

Andrea准备从网上购买一副新耳机. 但是，网上对该耳机的评论的总数较少，且该产品收到了许多差评：1星和2星的评论共占25%（如图17）.

网上对该耳机的评价

为了决定是否购买该产品，Andrea研究了1星和2星的所有评价，发现这些评价与产品的质量或功能没有关系. 她将1星和2星的差评进行汇总并概括（如表7）.

Andrea查看了所有用户的评价，发现只有1星和2星的评价用户对产品质量差、产品送达延迟或根本没有送达进行了评价. 试利用已知信息和电脑内置的计算器解答下面的问题.

问题4：（1）关于产品质量差的评价所占的百分比是多少？所有1星和2星的评价中，耳机延迟送达或根本没有送达所占的百分比是多少？

（2）Andrea担心耳机会延迟送达或不送货. 根据表7的信息，发生这样的情况的可能性有多大？试用分数或百分比的形式来表述你的答案.

2. 分析与思考

PISA测评一直贯彻从情境、内容和过程三个维度测评学生的数学素养. 数学情境是测试题的嵌入之处，数学内容是测试题的素材和载体，数学过程是将情境与内容相互联系进而解决问题的核心所在，三个维度相互关联、相互融合. 参照PISA2022数学示例中的情境、内容和过程，可在变与不变中寻得PISA测评理念的始终坚守和与时俱进.

（1）变中之不变——突出真实情境.

PISA2022数学情境仍突出真实性、丰富性、创新性. 真实性是情境性的首要条件，体现在将数学问题置于学生熟悉的真实生活环境之中，注重学生熟悉的、直接的生活经验在问题解决中的基础性和引导性作用. 情境越真实，越能有效地测评学生对生活、社会和科技的关注及真实体验. 例如，PISA2022数学示例中的智能手机、铺瓷砖、网上购物都是学生生活中的真实情境. 测试题就是学生真实的学习与生活的实际场景，紧紧围绕“数学无处不在，就在我们身边”的测评理念. 丰富性体现在测试情境能灵活、新颖地将测试内容巧妙地融入学生的个人生活、工作与休闲、社区与社会、科学与技术等丰富的问题情境中. 例如，PISA2022数学示例中智能手机的使用是学生的个人生活的真实情境，但作为社会层面来讲，更是社会情境普遍存在的现实情境;铺瓷砖属于未来职业的工作范畴，而网上购物更是现实生活中离不开的真实情境. 真实情境的多角度、全方位容易引起学生的探究兴趣，进而可测学生的真实性知识和技能. 创新性是情境性面向未来的体现，PISA测评是“为迎接未来的挑战”的测试，在测试题的独创性和新颖性上可谓耳目一新、前瞻十足. 例如，网络是当前学生感兴趣并且接触频繁的重要工具，网上购物更是学生喜爱并熟悉的真实情境，大数据的时代背景更为网上购物的鉴别和判断提供了有力依据，数学知识与技能的测评在真实与丰富中与时俱进、不断创新.80253BB6-C083-4B3F-B36D-B6DC0592CF56

结合数学内容、强调不同主题，使得数学内容与实际情境伴随着时代的变迁更好地结合，体现了时代更迭信息在PISA数学素养测评中的落地. 从PISA2022数学示例的数学情境、内容、主题分布（如表8）中可以看出，真实情境与具有时代性的主题内容融合是示例呈现的整体之貌. 虽然测评内容突出强调了四大主题，但PISA测评与时俱进的理念和方向一直未变，而是导向新时代的不断演进. 这“变”中之“不变”是PISA测评一直以来的始终坚守：为了迎接未来的挑战和发展.

（2）不变中的变——聚焦数学推理.

分析示例问题解决的过程，进一步看到PISA2022数学素养在多轮测评之后“不变”中的“变”. 首先，是对数学素养阐释与评估的加强. PISA2022评估将降低数学素养测试对解决纯数学问题的考查，也即降低了纯粹数学背景下的问题思考与解决. 测试示例在指向数学与实际情境的深层次紧密结合的基础上，更加关注数学的解释功能. 这本身体现的是数学的角色定位：用数学来解决实际问题，即淡化技能测试的导向，突出数学解释的功能. PISA强调“用数学”，重视数学知识和技能在社会生活中的应用，这也是现实数学教育的观点. 这与测试题的真实情境步调一致，利用情境搭建数学世界与现实世界的桥梁，利用问题聚焦数学建模的数学过程，在解决问题的过程中重视数学对现实世界的解釋、评估和预测功能. 例如，四个示例真实的问题情境都很好地指向“用数学去解释生活”，问题的真实情境使得数学的现实功能得以发挥. 其次，是对数学推理的重视. 从真实情境的现实问题，到用数学去解释建模，再到数学推理的过程，这实际上是问题解决的环环相扣、层层深入. PISA2022强调数学推理贯穿于问题解决的整个过程，对数学推理的考查落实到具体测试题目中，增强了表述、应用和阐释数学的解决问题的根本目的. 数学推理的六要素，针对数学概念、公式、关系、结构，涉及识别、领会、理解、应用，结合示例每道小题考查的数学推理要素进行分析，可得表9.

PISA2022对数学推理的重视体现在数学推理六个要素的覆盖全面，其中对“领会数学抽象与符号表征”“使用数学模型理解现实世界”和“理解数学结构及其规律”的要素考查比例是最高的，这也很好地印证了PISA2022对“理解数学”“用数学去理解现实世界”的关注和强调. 考查数学阐释过程中数学推理的比重最大，且对“理解数字系统及其代数性质”及“识别数量之间的函数关系”虽有考查，但对于纯数学技能的考查并非PISA的主旨. 数学表述、数学应用、数学阐释都不可缺失数学推理，数学推理是整个数学过程的轴心. 由图18可见，数学推理贯穿数学的表述、应用和阐释等过程，尤其在数学阐释中占比最多，数学应用与数学阐释两个过程中都全面涵盖数学推理的六个要素. 图19显示，数学内容的每个知识领域中都至少涵盖3个以上的数学推理要素，数学推理以内容为载体，与数学内容相互融合. 以示例“铺瓷砖”为例，从特殊到一般、由具体到抽象逐步升级的5个问题，都涉及“理解数学结构及其规律”和“使用数学模型理解现实世界”，其中4个问题涉及“领会数学抽象及符号表征”，这正是现实问题解决中数学推理的魅力聚焦.

三、变与不变中的启示

PISA2022沿袭了以往测评中的不变：关注现实世界的真实情境，顺应时代发展的共性理念，以未来生活需要的数学素养为根基，聚焦问题解决的数学过程. 亦在“不变”中谋“变”：不断强化和落实数学素养中的21世纪技能，不断修订数学素养的多维度考量，不断发展和突出数学素养与信息技术的整合. PISA2022在不变中始终坚守，在变中与时俱进.《义务教育数学课程标准（2011年版）》（以下统称《标准》）中明确指出：数学素养是现代社会每个公民应该具备的基本素养. PISA2022数学素养的测评对数学课程改革的启示是多方面的，涉及课程内容、课程规划、教学过程、教学评价等，但万变不离其宗，这个“宗”就是“以评促改”的有力武器和考试评价. 虽然理论上课程是先导，有什么样的课程，才相应有什么样的考试评价，但往往在实践中，考试评价历来被看作课程与教学的“指挥棒”，考试评价“指到哪里”，课程与教学就“打到哪里”. 而在考试评价中，最重要的莫过于试题，试题对课程与教学评价发挥着高度的导向作用. 通过对PISA2022数学示例的分析与思考，基于发展学生数学素养的诉求，需要在数学学业试题编制的“情境—问题—推理”中重点着力.

1. 重视真实情境的试题构建

PISA试题在真实情境中解决数学问题，囊括多种现实世界的真实情境，贴近学生的学习和生活实际. 学校数学课程体系，以纯数学的科学逻辑为主，体现的是数学知识和逻辑，对于真实世界的呼应较少. 作为现代公民，应该在关心社会、善于思考，用数学眼光看世界，用数学能力解释现实，用数学素养发展社会. 随着知识经济与信息社会的迅猛发展，学生面对的社会与时代也在瞬息万变，创设符合时代发展的数学情境是促使学生理解数学、理解现实的必然趋势. 基于情境视角落实数学素养的培养，首先应该重视真实情境的试题构建. 在目前的教学实践中，一线教师依然把情境看作数学学科知识的“外衣”，其根本原因就在于“考试不考或考得少”.《标准》中设置了“综合与实践”模块，但在真正的教学一线，很多教师都把这部分内容“大事化小，小事化了”了. 探及教师是否认可真实情境在数学学习中的重要性，答曰：无可厚非，毋庸置疑. 但为什么会出现理论与实践的不统一、思想与行动的不一致呢？究其根本原因，就在于考试指挥棒的作用发挥不到位. 如果在数学学业测评中加大真实情境的试题力度，进而蔚然成风，可想而知，教学一线会对真实情境的高度重视和大力实践.

2. 突出问题解决的试题主旨

数学一直很重要. 数学是以科学、技术和工程为创新原动力的经济发展基础，是理解现实世界和公民身份的基石. 不同行业对数学的需求越来越大，OECD发布的《不同行业中的数学》报告中指出，不同行业中的问题解决对数学的知识水平与能力提出了更高的要求，更加强调为适应未来社会与发展的数学素养. PISA指出：一个具有数学素养的人，能认识和理解数学在现实世界中所起的作用，能利用数学做出有根据的判断和决策，是一个具有建设性、参与意识和反思能力的公民. 数学应该成为年轻人的基础，就像运动、音乐和绘画一样，如果数学基础坚实，人类就会更坚实. 全球数学竞赛试题都是贴近实际生活的题目，“电商销售”“外卖小哥送货路径”等都是运用数学知识和能力解决的实际问题. PISA测评数学素养的根本目的在于问题解决，这些问题通常是有趣而富有挑战性的问题. 反思当前我们的数学测试题，考查纯数学知识与技能的题目仍占很大比例，偶尔配套的应用题也很难引发学生的兴趣，学生在知识学习的过程中见到并尝试解决真实问题的机会也较少，对跨学科、跨领域的真问题的真思考并不多，学以致用的“真刀真枪”的磨练尤显不足. 因此，数学课程改革中应突出问题解决的试题主旨，加强问题解决的试题导向，强化从“知识理解”到“问题解决”的试题评价理念.80253BB6-C083-4B3F-B36D-B6DC0592CF56

3. 加强数学推理的试题思维

PISA测评重视学生运用数学推理解决实际问题的能力. 在数学中，使用严密的逻辑推理从已知到结论需要“证到明处”“由因导果”“执果索因”，这就是最常用的数学推理. 数学教师在知识讲授上较为重视学生数学推理能力的培养，但在数学学业评价试题中对知识运用推理的体现还较为薄弱. 从学生视角来看，他们不喜欢简单计算或仅凭记忆就能解决的题目，反而很喜欢面对有趣、有意思的问题进行挑战，而有趣、有意思的题目中往往不可缺失的是数学推理. 最常用的七种寻找正确推理方法的推理工具是：① 比较;② 比例推理;③ 应用乘法量表;④ 拆分;⑤ 归并;⑥ 由简入繁;⑦ 概率推理和逻辑推理. 前三种属于数学表述的范畴，后四种属于数学应用的范畴，都属于数学解释与评估的范畴. PISA2022评估框架中对数学推理的要素内涵分析及这七种推理工具，都值得对数学学业试题的编制进行很好地反思与借鉴.

每一道数学测试题虽小，但其整体却关系到考试评价所起的“杠杆”作用，它衡量、调节甚至掌控着课程与教学的方向与实践. 任何一个知识都由相互联系的三部分组成：从哪里来，到哪里去，从“来”到“去”的过程. 在培养学生数学素养的课程与教学理念下，实际上这就是教学过程的三部曲：知识是怎样产生的？知识是什么？知识有什么用？其实，教学过程的三部曲与PISA测评的三个维度也是一致的：数学试题从现实情境中来，经历与数学内容紧密相连的数学推理过程，最后到达对现实问题的判断、解释、决策或评估. PISA2022是一条新的准绳，更是一面新的镜子. 参照准绳，我们应该严格自身的标准;对照镜子，我们应该更好地反观自身. PISA2022测评的示例，对编制与时俱进的各地数学中考试题提供了很好的思路，值得借鉴. 但路漫漫其修远兮，需要数学教育工作者们上下求索、砥砺前行.

参考文献：

[1]孙彬博，郭衎，邵珍红. PISA2021数学素养测评框架中的“21世纪技能”[J]. 数学教育学报，2019，28（4）：12-16.

[2]中華人民共和国教育部制定. 义务教育数学课程标准（2011年版）[M]. 北京：北京师范大学出版社，2012.

[3]桑贾伊·马汉贾恩，兹比格涅夫·马齐尼亚克，比尔·斯密特，等. 2021年PISA数学：来自CCR的分析[J]. 数字教育，2019，5（5）：83-92.80253BB6-C083-4B3F-B36D-B6DC0592CF56