既有拱桥光彩亮化改造后吊索的涡振性能

唐浩俊，邓周全，王泽文，李永乐，2

（1.西南交通大学桥梁工程系，四川成都 610031；2.风工程四川省重点实验室，四川成都 610031）

随着城市建设不断发展和人们精神文化需求日益增长，对既有建筑进行光彩亮化改造已成为一种趋势.大跨度桥梁是交通运输的纽带，亦是一道靓丽的风景线.在亮化改造的趋势下，它们又被赋予了新的使命，绽放出新的光彩.拱桥和斜拉桥都具有优美的结构外形，通常是一座城市的代表性建筑，也常成为光彩亮化工程的点睛之笔.

景观设计人员更加关心如何提高光彩照明效果，而科研人员则需要关心如何确保结构的抗风安全.李寿英与陈政清［1］研究了某斜拉桥的斜拉索安装亮化灯具后的驰振可能性，发现驰振的原因和两根平行于索轴线、直径12 mm 的钢丝有关.董国朝等［2］提出了一种流固耦合分析方法用以模拟和分析风致振动现象，在机理上解释了安装亮化灯具后驰振力的形成过程.徐升桥与刘永锋［3］介绍了京新上地斜拉桥的亮化方案，为了提高斜拉索的抗风性能，将亮化灯具嵌入了斜拉索的护套内.周傲秋等［4］指出灯具的存在导致斜拉索有较大概率发生驰振，而去掉灯具直接安装LED 点光源则可以降低斜拉索发生驰振的概率.邓周全等［5］通过风洞试验发现安装灯具后斜拉索的涡激共振现象有较大变化，其锁定风速会出现降低，并在较大的风向范围内具备驰振的可能性［6］.由此可见，亮化灯具的安装改变了索截面的气动外形，对索结构的抗风性能产生了很大的影响.相比气候条件变化对索截面气动外形的影响，例如覆冰或风雨的影响，亮化灯具造成的影响更加明显且持久.

亮化改造通常使用投光灯、泛光灯、点光源等.近年来，为了改善灯光效果，在拱桥的吊索或斜拉桥的斜拉索表面安装集成了LED 点光源的灯罩已成为主流趋势.通常，索截面为圆形，而灯罩截面可近似看作矩形，内部敷设电缆等设施.圆柱绕流和方柱绕流都是经典的流体力学问题.但是，这两种截面的旋涡脱落特性却有较大差异.

圆柱绕流的雷诺数效应非常突出，即使在高雷诺数下仍很明显［7-9］.圆形截面看似形状简单、规则，实则流场结构复杂、多变，涉及来流的分离、再附着、旋涡的形成等.矩形截面的流动分离点相对固定，流场特征与自身的宽高比相关［10-12］.可以预见，当这两种气动性能差异明显的截面靠近或结合在一起时，圆截面对雷诺数的敏感性，以及矩形截面对来流风向和自身宽高比的敏感性，都将成为影响组合截面流场结构的关键因素，使安装了亮化灯具柔性索的气动性能具有更多的不确定性.虽然前述提及的研究工作有助于我们掌握组合截面柔性索的风致振动行为，但目前的研究工作还非常有限，对组合截面气动特性的认识也还远不够.

本文以某座中承式系杆拱桥的亮化方案为背景.针对既有吊索的改造方案和新增吊索的设计方案，通过二维数值模拟对典型截面的旋涡脱落特性进行了分析，开展了节段模型风洞试验测试典型吊索的涡激共振响应，并据此对其余吊索的涡振性能进行了分析.研究结论可为相关的柔性索亮化工程设计和研究提供参考.

1 工程背景

某座中承式拱桥全长600 m，跨径100 m+400 m+100 m，拱顶至桥面69 m，如图1所示.全桥共54个吊点，相邻吊点间距12 m.各吊点处有两根柔性吊索，吊索间距为0.54 m，彼此间无连接，亮化灯具仅安装于其中一根吊索上.既有吊索内部采用标准强度为1 670 MPa 的镀锌平行钢丝，外部缠绕纤维增强聚酯带并设置紧贴的聚乙烯护套，直径为97 mm.考虑其中一副吊索，跨中处的既有吊索编号为M，其南侧吊索从跨中向端部依次编号为S1→S13，其北侧吊索从跨中向端部依次编号为N1→N13.为了达到更好的亮化效果，在既有吊索之间新增两处吊索，如图2 所示，采用标准强度为1 670 MPa 的镀锌平行钢丝，钢丝直径为11 mm，两支为一组.各组吊索从跨中向南、北两侧分别编号为S1′→S28′、N1′→N28′.

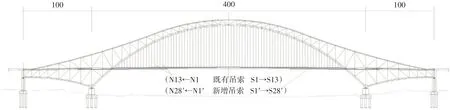
图1 桥梁立面布置图（单位：m）Fig.1 Elevation of the bridge（unit：m）

图2 既有吊索和新增吊索上的亮化灯具（单位：mm）Fig.2 Lighting fixtures for the existing hanger and the additional hanger（unit：mm）

亮化灯具由灯罩、LED 灯、电缆三个部分组成.其中，灯罩沿索轴向通长布置；LED 灯间隔111 mm嵌于灯罩表面，朝桥面外侧凸出；电缆线置于铝制灯罩的内部为各LED灯供电.对于既有吊索，亮化灯具通过间隔的抱箍附于其中一根上.灯罩顺桥向宽度H1=59.6 mm，横桥向宽度B1=34.4 mm，灯罩与吊索之间存在约10 mm 的间隙.灯罩面积与吊索面积之比达到了27.7%，显著改变了截面的气动外形.对于新增吊索，亮化灯具包裹住两根钢丝.灯罩顺桥向宽度H2=67.6 mm，横桥向宽度B2=42.9 mm.

2 截面的旋涡脱落特性

2.1 数值模型及无关性验证

本节基于计算流体力学软件FLUENT，通过二维计算模拟了吊索截面的绕流特性.如前所述，既有吊索和新增吊索上的亮化灯罩沿索轴方向通长布置，但LED灯间隔嵌于灯罩表面并向外凸出.为了考虑局部LED 灯对截面旋涡脱落特性造成的影响，分别建立了有灯罩及其上LED 灯的计算截面和有灯罩但不含其上LED 灯的计算截面.图3（a）给出了既有吊索计算截面的数值模型，同时包含同一吊点另一根不装灯具的吊索，缩尺比为1∶1，以避免雷诺数的影响.计算区域为长方形，为减小壁面对圆柱绕流的干扰，上下边界之间的距离略大于60D，对应的阻塞率约3.3%，圆截面中心距左侧入口边界18D，距右侧出口边界50D，其中D为吊索的直径.图3（b）给出了新增吊索计算截面的数值模型，同样按1∶1 缩尺比建立.上下边界之间的距离约为50H2，对应的阻塞率约2%，灯罩中心距左侧入口边界20B2，距右侧出口边界70B2，其中H2为灯罩顺桥向宽度，B2为灯罩横桥向宽度.

图3 计算区域及网格划分Fig.3 Computational domain and grid partition

采用非定常计算，湍流模型为SSTk-ω模型；用SIMPLEC 算法解决动量方程中速度分量和压力的耦合问题；动量方程、湍动能方程及湍流耗散率方程均采用二阶离散式.以无LED 灯的既有吊索截面和新增吊索截面为例进行时间步长无关性计算，取风向角为0°，计算风速为15 m/s，采用不同的时间步长进行模拟，提取各截面的平均阻力系数CD-mean和均方根升力系数CL-RMS.对于既有吊索，将安装了灯具的索截面标记为A，未安装灯具的索截面标记为B；对于新增吊索，其截面标记为C.计算结果如表1所示，为了便于比较各个截面的气动力系数，其特征尺寸均取既有吊索的索径.

表1 计算步长对结果的影响Tab.1 Effects of time steps on results

对于这三个计算截面，当时间步长分别达到0.000 5 s、0.000 1 s、0.000 1 s后，继续减小时间步长对其气动力系数的影响较小.为兼顾计算精度与效率，后续计算取时间步长为0.000 1 s.此时，索B（圆截面）对应的雷诺数约为105，其阻力系数平均值为1.03，与多篇文献［8，13-17］通过风洞试验或数值模拟得到的结果范围1.0～1.2相符.

基于该时间步长，进一步对网格数量无关性进行验证.在前述计算中，两个模型的网格数量分别为18.36 万和14.90 万（标记为取定工况）.现通过调整壁面网格宽度、厚度及增长率，将两个模型的网格数量减少至14.10万和11.63万（标记为工况减1），再减少至10.15 万和8.21 万（标记为工况减2）；增加至22.34 万和18.51 万（标记为工况加1），如表2 所示.可以看到，前述计算中网格数量足够，继续增加网格对结果几乎没有影响，而网格数量减少后计算结果出现了一定程度的变化.

表2 网格数量对结果的影响Tab.2 Effects of mesh numbers on results

2.2 外附矩形截面的旋涡脱落特性

既有吊索外附矩形灯罩后，其截面的气动力系数发生了很大变化.表1 中仅考虑了来流风垂直于桥轴线，即风向角为0°的情况.考虑到来流风向的不确定性，进一步计算-30°～+30°风向角时截面的气动力系数.同一吊点处两根吊索中仅一根外附有矩形灯罩，故正、负风向的结果不相同，定义负风向来流在顺桥方向先流经有外附灯罩的吊索，正风向来流在顺桥方向先流经无外附灯罩的吊索.以吊索圆心作为气动力的监控点，有外附灯罩吊索截面（以下简称组合截面）的平均阻力、升力系数如图4 所示.其中，气动力为吊索与灯罩气动力之和，特征尺寸取吊索直径，坐标系选用体轴坐标系.组合截面升力系数均方根值如图5所示，并对升力时程曲线进行了频谱分析，根据其卓越频率换算了对应的斯托罗哈数St.

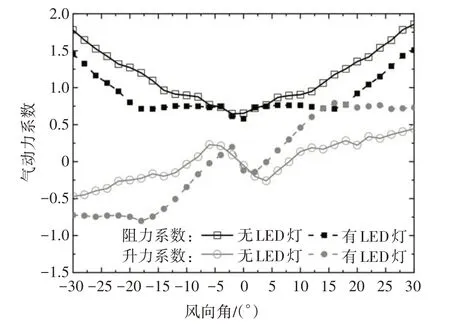
图4 既有吊索的平均气动力系数Fig.4 Mean aerodynamic coefficients for existing hangers

图5 既有吊索的升力系数均方根值和斯托罗哈数Fig.5 RMS lift coefficients and St for existing hangers

由计算结果可以看到，灯罩上局部LED 灯对组合截面的平均气动力系数产生了较大的影响.当风向角在0°附近时，有、无LED 灯的组合截面的平均气动力系数相近.当风向角达到±4°时，两组合截面的平均气动力系数开始出现差异.随着风向角的增大，两者差异也逐渐增大，有LED 灯组合截面的平均阻力系数基本保持不变；而平均升力系数变化更明显，其斜率大于无LED灯组合截面.当风向角达到-18°、+16°时，有LED 灯组合截面的平均阻力系数开始增加，而平均升力系数基本不变.随着风向角进一步增大，两组合截面的平均气动力系数趋于一致.

安装灯罩后组合截面升力系数均方根值在较大的风向角范围内明显降低.0°风向角时，有LED 灯组合截面的降幅更大，达到了89.4%；无LED 灯组合截面的降幅要小些，也达到了39.6%.此外，LED灯对截面的旋涡脱落频率影响显著，达到了两倍的差异，无LED灯组合截面的St数明显下降.

图6 给出了0°风向角时，组合截面升力达到最大（方向向上）及最小（方向向下）时流场的涡量云图.由图6 可知，来流在灯罩两侧的倒角处发生分离并在吊索表面再附着，这相当于增加了组合截面的顺风向宽度.尾流区域内，旋涡被明显拉长，脱落位置的后移使截面升力系数的波动减小.图6 中还标出了组合截面尾流区域内的旋涡，从上、下侧脱落的旋涡分别标注为“上”“下”，并按脱落先后标注编号.灯罩上有、无LED 灯两种组合截面的旋涡脱落频率不同，尾流中旋涡分布及发展规律也存在差异，降低了吊索发生涡激共振的可能性.

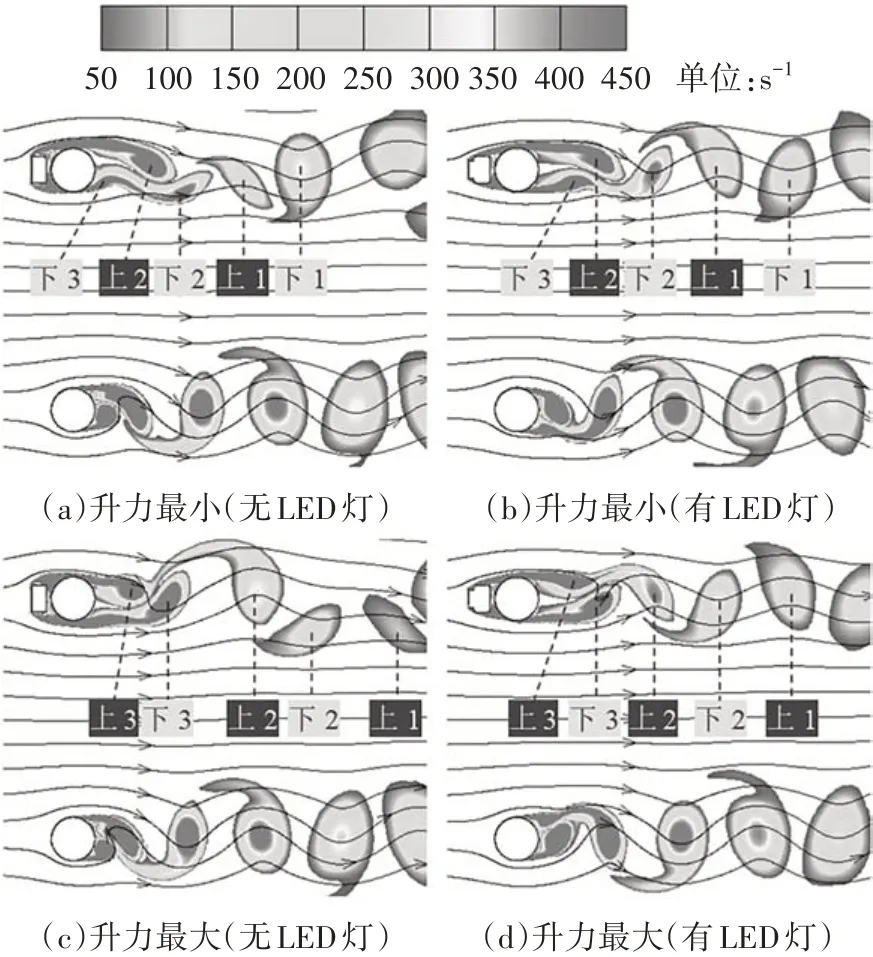
图6 涡量云图（0°风向角）Fig.6 Contours of the vorticity（with 0°yaw angle）

当风向角增大至+4°，或减小至-6°时，无LED 灯组合截面的旋涡脱落频率突然增大.随着风向角绝对值进一步增大至10°～14°，有、无LED 灯组合截面的升力系数均方根值与斯托罗哈数均比较接近.随后，两组合截面的旋涡脱落特性再次出现差异，直到风向角绝对值接近30°时，它们的升力系数均方根值与斯托罗哈数再次接近.图7 给出了30°风向角时，组合截面升力达到最大及最小时流场的涡量云图.可以看到，斜向来流风可穿过灯罩与吊索之间的空隙，弱化了LED 灯对流场结构的影响.此时，灯罩上有、无LED 灯两种组合截面的旋涡脱落频率相近（见图5 中的斯托罗哈数St），尾流中旋涡分布及发展规律也更加同步，这增大了吊索结构发生涡激共振的可能性.

图7 涡量云图（30°风向角）Fig.7 Contours of the vorticity（with 30°yaw angle）

2.3 外包矩形截面的旋涡脱落特性

新增吊索外包灯罩后，其截面的气动外形相当于矩形.考虑到来流风向的不确定性，计算了0°～+30°风向角时截面的气动力系数，并考虑了有、无LED 灯的情况.由于计算区域内仅有一个截面，其气动力系数的分布具有对称性，即正、负风向角对应的结果一致.以灯罩形心作为气动力的监控点，计算结果如图8、图9所示.

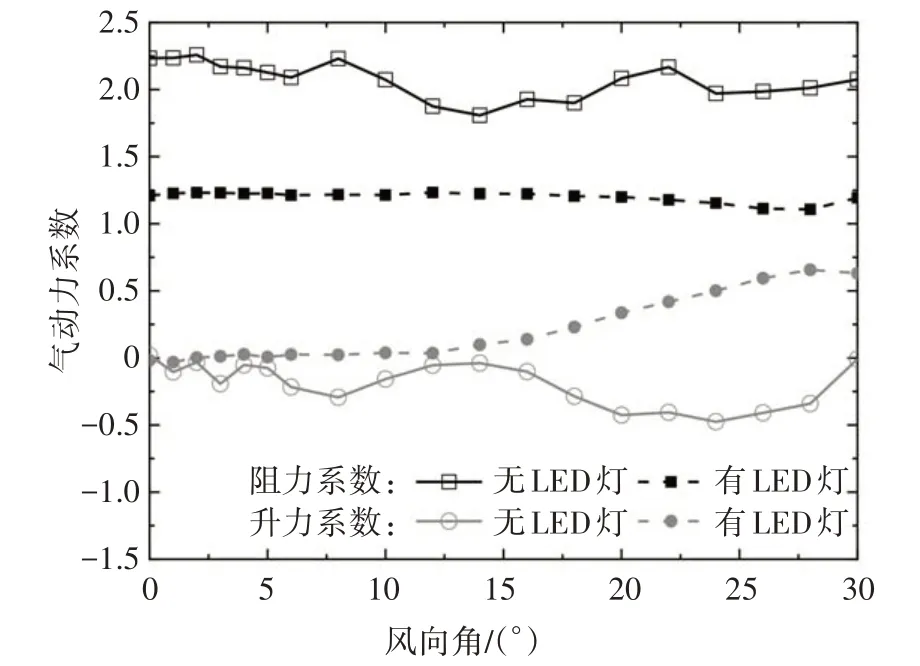
图8 新增吊索的平均气动力系数Fig.8 Mean aerodynamic coefficients for additional hangers

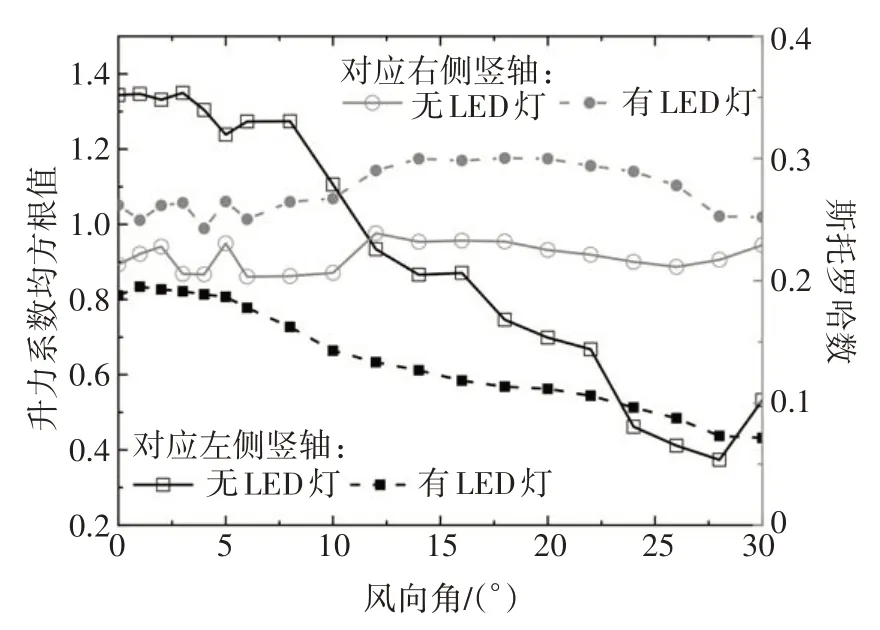
图9 新增吊索的升力系数均方根值和斯托罗哈数Fig.9 RMS lift coefficients and St for additional hangers

新增吊索截面的平均阻力系数和平均升力系数如图8 所示.为了便于和上一节的计算结果进行比较，特征尺寸仍取既有吊索直径，坐标系选用体轴坐标系.当风向角为0°时，两截面阻力系数差异较大，LED 灯的存在使截面的阻力系数平均值降低了45.9%；两截面升力系数平均值均接近零.随着风向角增大，两截面阻力系数平均值的差异有所减小.但是，当风向角达到14°时，阻力系数的差异又再次增大，且升力系数的差异也逐渐增大.

新增吊索截面的升力系数均方根值如图9 所示.同时，对升力系数时程曲线进行了频谱分析，根据其卓越频率换算了对应的斯托罗哈数St.两截面升力系数均方根值的差异在0°时最明显，随着风向角从0°增大至30°，两者差异逐渐减小.St数随风向角的变化呈现相反的规律，当风向角介于0°～5°时，两截面的旋涡脱落频率较为接近.随着风向角增加，两截面的旋涡脱落频率的差异增大，但当风向角接近30°时，差异又逐渐减小.

图10 给出了0°风向角时，新增吊索截面升力达到最大（方向向上）及最小（方向向下）时流场的涡量云图.虽然两个计算截面的旋涡脱落频率较为接近，但涡量云图却有较大的差异.无LED 灯的截面近似矩形，来流风在灯罩两侧倒角处发生了分离，使截面上、下侧的涡量较大，即升力系数均方根值较大.同时，来流分离所导致的旋涡具有较大的尺寸和强度，且紧贴截面右侧，使阻力系数较大.尾流区域内，脱落旋涡的分布较为杂乱.有LED灯时，来流风在LED灯两侧就发生了分离.LED 灯与灯罩之间形成的凹角起到了一定的导流作用，使截面上、下侧的涡量降低，即升力系数均方根值减小.同时，尾流侧旋涡的尺寸和强度有所减小，使截面阻力系数减小.尾流区域内，脱落旋涡的分布也变得规则.

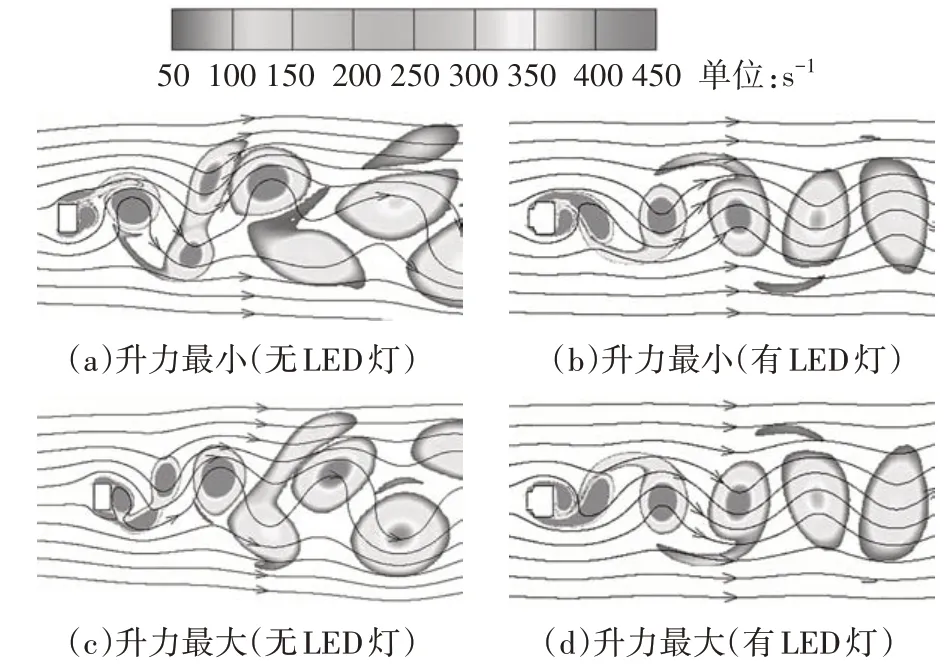
图10 涡量云图（新增吊索）Fig.10 Contours of the vorticity（for additional hangers）

3 吊索的涡振响应分析

上一节通过二维数值模拟研究了亮化灯具对吊索截面旋涡脱落特性的影响，考虑了灯罩上有、无LED 灯两种组合截面，并定性评价了不同风向角下两者尾流中旋涡分布及发展规律的异同.实际上，局部LED 灯对流场的影响是三维的，还有局部抱箍的影响.本节将通过风洞试验对前述现象进行验证，并进一步评价吊索的涡振性能.

3.1 既有吊索的涡振响应

结构的涡激共振响应与结构的模态频率有密切联系.既有吊索安装亮化灯具后，质量的变化，会导致其模态频率发生变化.

采用通用有限元软件ANSYS 对各既有吊索的模态频率进行了计算分析，用LINK10 单元模拟吊索，吊索内力通过设置初应变的方式施加.各吊点处含有两根吊索，但两根吊索之间没有相互连接，故建模时只考虑其中一根.亮化灯具的质量需考虑灯罩和电缆两部分，通过质量点单元进行模拟.安装亮化灯具前后，各吊索的一阶模态频率如图11 所示.其中，横轴为吊索的编号.可以看到安装亮化灯具后吊索的模态频率略有减小.

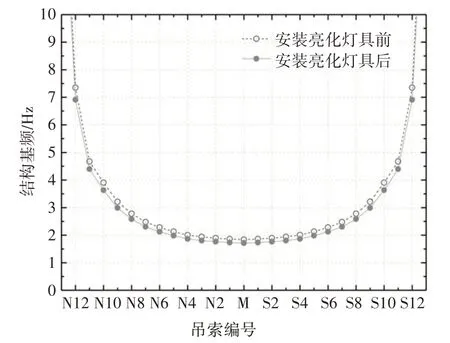
图11 既有吊索的基频Fig.11 Fundamental frequencies of the existing hangers

试验在西南交通大学XNJD-1 风洞高速试验段进行，通过节段模型动力试验测试既有吊索安装亮化灯具后的涡振性能.试验模型长度2.095 m，按照1∶1 的几何缩尺比制作，即吊索直径为97 mm，灯罩高34 mm，宽60 mm，根据实际间隔在模型上布置LED 灯模型，如图12 所示.以跨中处的吊索为模拟对象，考虑到实际吊索的质量偏大，降低了模型的质量，具体参数见表3.其中，无灯模型为没有安装灯具的吊索模型，其测试结果仅作为对比参考，没有调整测试系统的阻尼比；有灯模型为安装灯具的吊索模型，略增大了测试系统的阻尼比，使模型与原型的Sc数（Sc=4πmξ/ρD2，其中m为每延米质量；ξ为阻尼比；ρ为空气密度；D为横风向特征尺寸，取圆截面直径）比值为0.81.

图12 试验模型（既有吊索）Fig.12 Experimental model（for existing hangers）

表3 既有吊索试验模型参数Tab.3 Experimental parameters for existing hangers

试验中采用激光位移计测试了安装亮化灯具的吊索的位移响应.测试风向角包括0°、15°、30°、45°，吊索的竖向振幅随试验风速的变化规律如图13 所示.其中，0°风向角时来流风垂直于桥轴线.当风向角为45°时，考虑到同一吊点处两根吊索相互之间可能产生的气动干扰，试验中在测试索的上游设置了另一根未安装亮化灯具的吊索.

图13 竖向振幅随风速的变化Fig.13 Vertical displacements versus the wind speed

当风向角为0°时，无灯具吊索在风速为1 m/s 时出现了涡激共振现象，安装灯具后的吊索在试验风速范围内未出现明显的涡激共振现象.结合上一节数值模拟的结果可知，安装灯罩后截面升力的均方根值明显减小，且LED 灯的间隔布置以及抱箍的设置使得不同截面脱落旋涡的强度、频率不一致，这些差异降低了吊索整体发生涡激共振的可能性.

在斜风来流作用下，安装灯具后的吊索则出现了明显的涡激共振现象.具体情况如下：当风向角增大至15°时，吊索在风速1.20 m/s 左右发生了涡激共振现象，但振幅有限，最大值为3.9 mm.当风向角增大至30°时，吊索在风速1.27 m/s 左右发生了涡激共振现象，且振幅明显增加，最大值为117.8 mm，达到了吊索直径的1.21 倍.当风向角继续增大至45°时，受上游侧未安装灯具的吊索尾流的影响，安装灯具的下游索在风速1.4 m/s 左右发生了涡激共振现象，振幅虽有减小但仍然明显，最大值为38.1 mm，达到了吊索直径的0.39倍.

试验中以跨中处最长的吊索为对象进行了测试，据此换算其余吊索的涡振锁定风速.以风向角30°为例，试验索在1.27 m/s 风速下发生了明显的涡振现象，其竖向位移时程的卓越频率为1.750 Hz.取吊索直径为特征尺寸，可得组合截面的斯托罗哈数St为0.134.基于St相同，可根据其他吊索安装灯具后的模态频率换算对应的涡振锁定风速，如图14 所示.其中，吊索的各阶频率按照弦理论公式进行计算.由计算结果可知，安装亮化灯具后，吊索的模态频率略有降低，但组合截面的斯托罗哈数明显减小，故导致各吊索的涡振锁定风速有所提高.跨中附近吊索基频所对应的涡振锁定风速小于2 m/s，此时来流风能量有限，且通常较紊乱，在一定程度上会弱化涡振响应，但应注意可能的高阶涡振.

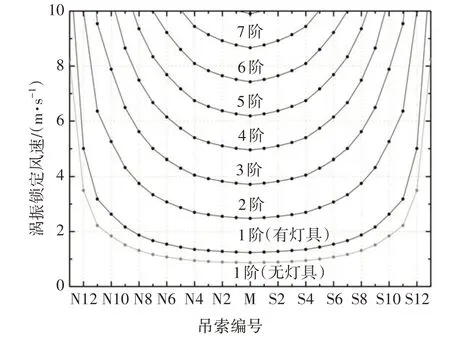
图14 不同吊索的涡振锁定风速Fig.14 Lock-in wind speeds of different hangers

3.2 新增吊索的涡振响应

新增吊索不参与结构受力，其主要作用是固定亮化灯具.因此，新增吊索的面积远小于既有吊索，灯具的安装方式也不同于既有吊索.如前所述，新增吊索被亮化灯具的外壳所包裹，其刚度由吊索提供，而气动力由亮化灯具决定.为了保证新增吊索上亮化灯具的正常工作，其抗风稳定性也是需要关注和考虑的.假设新增吊索的初始应变与邻近位置处既有吊索一致，由此确定新增吊索的初始张拉力T0.然后，将此张拉力分别折减至0.75、0.50、0.25倍，并通过弦理论公式计算新增吊索的模态频率，如图15所示.

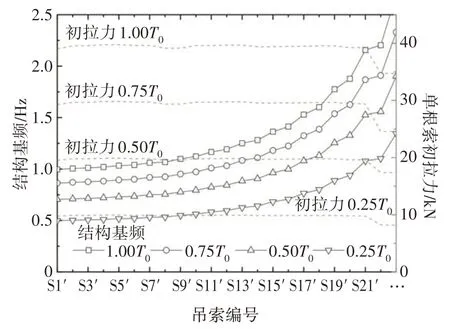
图15 新增吊索的基频Fig.15 Fundamental frequencies of the additional hangers

新增吊索的模态频率低于既有吊索，跨中处吊索长度最大、模态频率最小.较大的初始张拉力可以在一定范围内提高新增吊索的模态频率，但其值仍然小于既有吊索.需要注意的是，虽然张拉力的具体数值不大，但由于新增吊索净面积较小，过大的张拉力可能导致新增吊索应力过大，且对两端的约束也会提出更高的要求.

在上一节的分析中，已得到新增吊索截面的斯托罗哈数St，可根据各新增吊索的模态频率换算对应的涡振锁定风速.其中，特征尺寸采用了既有吊索的直径，即97 mm.在数值计算中，考虑了灯罩上有、无LED灯两种情况，当风向角为0°时，无LED灯截面的St=0.21，有LED 灯截面的St=0.26，据此区间换算得到的涡振锁定风速如图16 中虚线所包络的范围；当风向角为30°时，无LED 灯截面的St=0.23，有LED灯截面的St=0.25，据此区间换算得到的涡振锁定风速如图16 中实线所包络的范围.由前述关于既有吊索的分析可知，在某风攻角来流作用下，若有、无LED 灯这两种截面的旋涡脱落特性接近，则吊索更容易发生涡激共振现象.对于新增吊索而言，30°风向角下两截面的斯托罗哈数更为接近，吊索发生涡激共振的可能性更高.总体来看，新增吊索的基频较低，对应的涡振锁定风速很小，但需要注意可能出现的高阶模态涡激共振现象.此外，由于新增吊索非常轻柔，除了涡振响应外，其在脉动风作用下的抖振问题也不容忽视.为了提高其抗风性能，有必要进行气动优化设计，或增加横向连接索等结构优化措施，利用相邻的既有吊索提供一定的约束，如图17 所示，但措施具体效果还有待进一步验证.

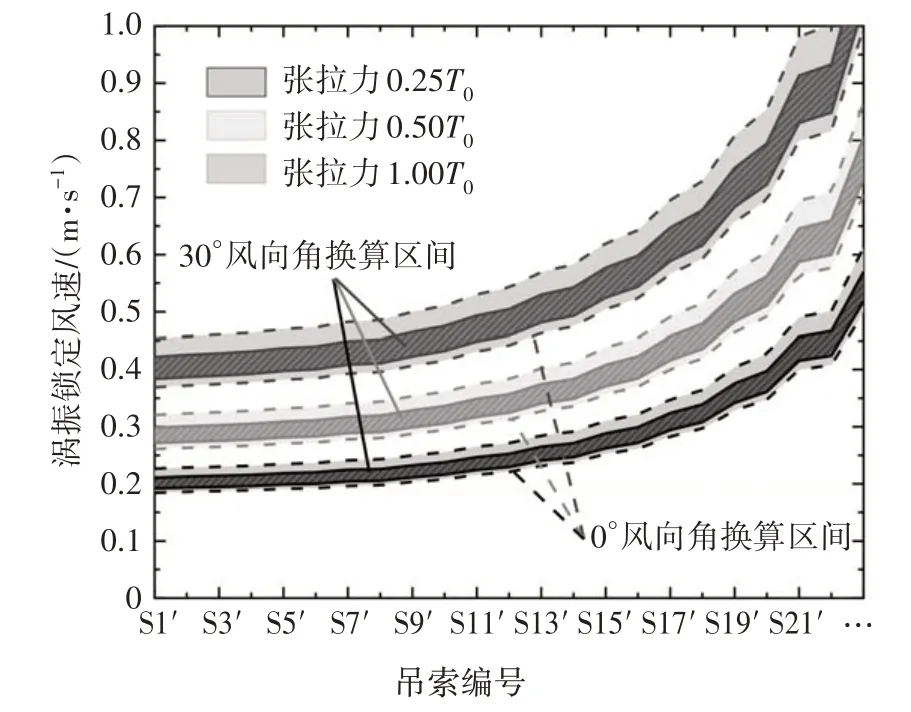
图16 新增吊索基频对应的涡振锁定风速Fig.16 Lock-in wind speeds of the additional hangers corresponding to the fundamental frequencies

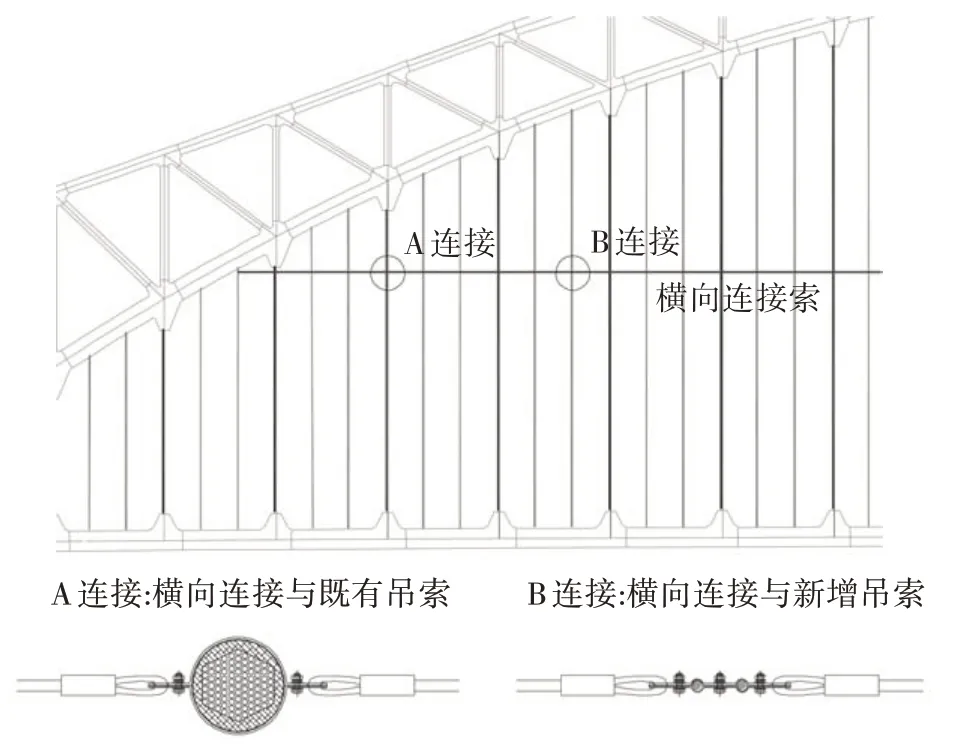
图17 增设横向连接索Fig.17 Additional cross cable in the transverse direction

4 结论

本文以某座中承式拱桥的亮化方案为背景，研究了吊索涡振性能的改变，得到以下主要结论：

1）亮化改造使既有吊索的气动外形发生根本性改变，相当于圆形和矩形构成的组合截面.组合截面的绕流行为受风向角影响明显，当风向角较小时，来流在灯罩两侧倒角处发生分离并在吊索表面再附着，减小了旋涡脱落的强度和频率.当风向角较大时，来流经过吊索和灯罩之间的间隙并产生加速效应，增强了旋涡脱落的强度.

2）当来流垂直于桥轴线时，安装灯具后既有吊索发生涡激共振的可能性较小.究其原因，一方面是组合截面升力均方根值明显减小，另一方面是灯罩上间隔设置的LED 灯使索轴向不同截面的旋涡脱落频率、强度出现了差异.当来流与桥轴线呈现一定夹角时，安装灯具后既有吊索发生涡激共振的可能性增大.这是因为斜风作用下组合截面升力均方根值较大，且LED灯对流场的影响有所减弱.

3）因不参与结构受力，新增吊索非常轻柔，其基频对应的涡振锁定风速很小，但吊索在高风速下的高阶模态涡振问题及抖振问题不容忽视.增大初拉力对新增吊索模态频率的提升有限，还可能导致吊索自身及两端连接件的强度问题.为了提高其抗风性能，在设计时有必要考虑抑振措施.

4）既有吊索安装亮化灯具后，两种计算截面的升力系数在0°风向角附近出现了负斜率，且对应的驰振临界风速很低，但在试验中未观测到模型的驰振现象.这可能与不同截面旋涡脱落特性的差异有关，使吊索整体的准定常气动特性与各截面有所差异，还应该开展三维动态模拟进一步研究.