摩擦阻尼器-拉索系统振动特性试验研究

周海俊，何纪元，杨夏†，向宁

（1.深圳大学城市智慧交通与安全运维研究院，广东深圳 518060；2.广东省滨海土木工程耐久性重点实验室（深圳大学），广东深圳 518060）

斜拉索是斜拉桥的主要受力构件，由于其质量轻、阻尼低、柔度大，故极易在外界激励下产生各种类型的振动［1-5］.持续大幅振动会引起诸多次生问题，如拉索锚固端疲劳破坏、保护套开裂等，从而缩短斜拉索的使用寿命，带来不可估量的经济损失.目前拉索减振已成为大跨径斜拉桥建设和维护中亟须解决的关键问题之一.工程中常采用的斜拉索减振措施包括机械措施（增加阻尼器）、结构措施（安装辅助索）和气动措施等［6-7］.阻尼器具有减振性能稳定等突出优点，在工程应用中被普遍采用［8-9］.常见的线性黏滞阻尼器往往针对某一阶特定模态进行优化，但拉索的振动往往存在多阶模态耦合，线性黏滞阻尼器并不能很好地抑制拉索多模态振动.已有研究表明摩擦阻尼器对于各阶模态均可达到最大模态阻尼比，故可更有效地抑制阻尼器-拉索系统多模态振动［10］.

已有较多学者采用不同的方法（如有限元建模分析、谐波平衡法等）对摩擦阻尼器-拉索系统进行研究，初步揭示了摩擦阻尼器的非线性作用机制并确认其可以有效地抑制拉索振动［10-12］，但由于摩擦阻尼器的强非线性，影响摩擦阻尼器减振效果的因素较多，非常有必要进行摩擦阻尼器-拉索系统模型振动试验并分析其减振性能，以便进一步优化摩擦阻尼器，使之达到更好的减振效果.本文设计制作了铜-钢金属摩擦阻尼器，并进行了摩擦阻尼器-拉索系统模型的自由振动和强迫振动试验，研究分析摩擦阻尼器的减振效果及相关参数的影响.

1 拉索模型

本文取苏通大桥Z16 号拉索为原型，拉索弦长303.95 m，索力4 178.7 kN，单位长度质量68.6 kg/m，倾角36.34°，基频0.406 Hz.拉索模型缩尺比为1∶20，原型索与拉索模型的索重之比约为两者的索力之比，原型索与拉索模型具有较高的相似性.拉索模型的参数详见表1.为使模型拉索的基频和原型拉索满足相似律，拉索模型每隔10 cm 安装一个配重铜块，质量为86.7 g.该拉索模型较细长，因此本文不考虑抗弯刚度的影响.

表1 拉索模型参数表Tab.1 Parameters of cable model

2 摩擦阻尼器构造及标定试验

2.1 摩擦阻尼器模型

图1 所示摩擦阻尼器模型主要由摩擦片、拧紧螺栓、索夹、固定支架以及环形支架组成.摩擦片采用黄铜片，索夹、拧紧螺栓、垫板、支架材料均采用Q235 钢材.摩擦片嵌固在索夹上，拧紧螺栓固定在支架上，旋紧螺栓使得螺栓与摩擦片之间产生挤压力，当拉索振动时，索夹随之振动，摩擦片与拧紧螺栓产生相对运动，从而产生摩擦力.通过调节拧紧螺栓与摩擦片之间的挤压力可调节摩擦力的大小.

图1 摩擦阻尼器模型Fig.1 The friction damper model

摩擦阻尼器模型设计时首先需确定摩擦力大小.摩擦阻尼器的临界工作振幅Acrit与摩擦力F0的关系见式（1）.［11］

式中：i为模态阶数；l1为摩擦阻尼器距离拉索下锚固端的距离；T为拉索张力；L为拉索长度.临界工作振幅是指摩擦阻尼器刚开始工作时对应的拉索振幅.可见临界工作振幅与模态阶数成反比关系.

本文中l1=0.752 5 m（l1/L=0.05），为安全起见，一阶临界工作振幅不宜过大，由式（1）可以确定摩擦力F0与一阶临界工作振幅Acrit的对应关系如表2所示.

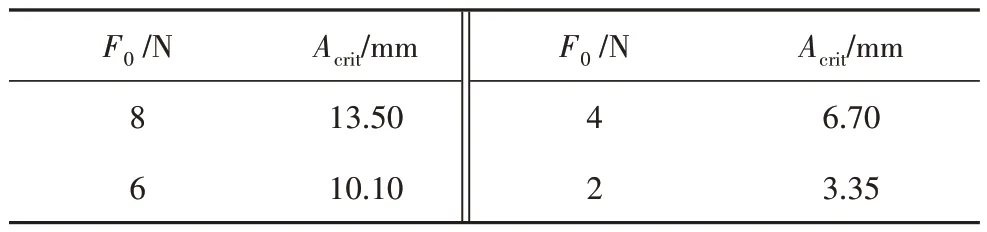
表2 F0 与Acrit 的对应关系Tab.2 The relationship between friction force F0 with the critical amplitude of the first mode Acrit

2.2 摩擦力标定试验

采用微机控制电子万能试验机进行标定试验，量程0～10 kN，精度为±0.5%，力传感器量程0～ 50 kg.扭力起子型号LTDK-1.5，量程0.01～0.15 N·m，精度为±5%.先将索夹与连接件通过螺栓固定，再通过插销将连接件与电子万能试验机拉伸辅具连接固定，通过扭力起子对拧紧螺栓施加扭矩.单向拉伸加载控制方式为位移控制，加载速率为1 mm/min，当拉力载荷克服摩擦阻尼器模型的静摩擦力后，摩擦片开始匀速滑动，此时拉力与滑动摩擦力的大小相等.

设定拧紧螺栓扭矩T0的5个工况分别为0.05 N·m、0.10 N·m、0.15 N·m、0.20 N·m、0.25 N·m，图2 所示为其中3 个工况的摩擦力时程曲线.可见，摩擦力时程曲线的变化规律基本相似，从t=0 时刻开始，摩擦力先快速增长后趋于稳定.取摩擦力时程曲线水平段的平均值为该扭矩对应的摩擦力大小.

摩擦力F0随扭矩T0的变化如图3 所示，线性回归得：

决定系数R2=0.979.

3 摩擦阻尼器-拉索模型

3.1 试验设备及测点布置

图4（a）所示为摩擦阻尼器-拉索系统模型试验示意图.力传感器安装在上锚固端，4 个激光位移传感器测量拉索模型面内振动位移，分别安装在拉索模型摩擦阻尼器位置处、距下锚固端L/6 处、L/4 处、L/2 处，加速度传感器安装在距下锚固端L/3 处.图4（b）为摩擦阻尼器-拉索系统模型实物图.试验设备规格详见表3.

表3 试验设备Tab.3 Testing facility

图4 摩擦阻尼器-拉索系统模型Fig.4 Friction damper-cable model

3.2 试验过程及数据处理方法

激振器安装在距离拉索模型下锚固端0.1L处，拉索上固定有法兰克夹，采用尼龙线连接法兰克夹和激振器激振杆.首先对摩擦阻尼器-拉索系统模型进行正弦扫频测得含有系统各阶模态响应的位移时程曲线，通过快速傅里叶分析得到各阶频率.将测得的系统各阶频率输入为激振器激振频率进行激振，待拉索模型振动稳定后剪断尼龙线，采集系统自由振动衰减运动时程数据.最后，通过激振器进行正弦扫频对摩擦阻尼器-拉索模型进行强迫振动激励并记录得到响应振幅.本实验中数据采样频率为500 Hz.

采用快速傅里叶分析对拉索自由振动的加速度数据进行分析得到拉索的振动频率；根据滤波后的自由振动位移衰减时程数据计算对数衰减率δ，其计算公式见式（3）［13］.

式中：Aj、Aj+k分别为相隔k个振动周期的j时刻与j+k时刻的振幅.

4 试验结果

4.1 拉索模型自由振动

本文相隔50 个振动周期计算得到拉索模型面内一阶自由振动的对数衰减率，其平均值为0.39%.考虑拉索垂度的自振频率fi计算公式见式（4）［14］.

表4 所示为拉索模型面内前五阶自振频率试验值与理论值的比较.可以看出，面内自振频率试验值与理论值的误差较小，理论值略大于试验值的原因在于力传感器安装于拉索模型上端，其张力值相较于张紧弦理论的张力值偏大.

表4 面内前五阶自振频率试验值与理论值比较Tab.4 The first five test and theoretical in-plane mode frequencies

4.2 摩擦阻尼器-拉索模型自由振动

摩擦阻尼器-拉索系统模型自由振动试验设置摩擦力F0工况为2 N、3 N、4 N、5 N.图5 所示为摩擦阻尼器-拉索模型L/2处面内一阶自由振动衰减曲线（阻尼器安装位置l1/L=0.05，摩擦力F0=5 N）.拉索L/2 处面内一阶自由振动衰减曲线在摩擦阻尼器将拉索锁住之前近似呈线性衰减.自由振动衰减到临界工作振幅（约为8 mm）时，拉索在摩擦阻尼器位置处振动的恢复力小于摩擦力，此时摩擦阻尼器将拉索“锁住”并停止工作，拉索通过内阻尼耗散振动能量，由于拉索内阻尼极小，拉索振动幅值衰减极慢.

图5 一阶自由振动位移衰减时程曲线（l1/L=0.05，F0=5 N）Fig.5 First mode free vibration displacement decay curve（l1/L=0.05，F0=5 N）

其他摩擦力工况在L/2 处面内一阶自由振动衰减曲线变化趋势与图5相似，故不再赘述.图6（a）所示为在不同摩擦力工况下一阶对数衰减率-振幅关系曲线的比较，对数衰减率为相隔2 个振动周期计算得到.可见随着振幅的逐渐减小，一阶对数衰减先逐渐增大至最大值，然后急剧下降至接近于0.随着摩擦力的增大，一阶对数衰减率-振幅关系曲线向右平移，对数衰减率最大值无明显变化，临界工作振幅逐渐增大.

图6 一阶对数衰减率-振幅关系Fig.6 First mode logarithmic decay rate-amplitude

在给定振幅和频率下，令摩擦阻尼器在一个周期内所做的功与等效线性黏滞阻尼器所做的功相等［15］，可得到对数衰减率δ与振幅A的关系式，见式（5）.

将本试验中的参数L、T、l1/L代入式（5），得到对数衰减率δ随振幅A变化的曲线如图6（b）所示.对比图6（a）、图6（b），可见对数衰减率试验值和理论值随拉索振幅变化的趋势一致.

公式（5）中，对振幅A求导并令导数为0，可得到对数衰减率的最大值δmax，发现δmax与F0无关，这与图6（a）试验结果相符.试验结果相较于理论值，各工况下最大对数衰减率偏大，临界工作振幅偏小.其原因是摩擦阻尼器具有强非线性，而模态阻尼比是基于线性黏滞阻尼假设，用模态阻尼比来评价非线性的拉索-摩擦阻尼器系统的阻尼会导致一定的误差.

图7 所示为面内一阶加速度时程曲线与频谱图（l1/L=0.05，F0=5 N）.可见摩擦阻尼器-拉索系统面内一阶振动含有多阶模态频率成分，图中标出了一、二、三阶振动频率.对摩擦阻尼器-拉索系统自由振动的一阶加速度数据做连续小波变换分析表明，一阶频率在12 s 时发生了小幅度增大的“偏折”，这与阻尼器将拉索锁住导致频率增大的现象吻合；进一步分析表明，一阶振动频率在拉索锁住之前就有随时间而增大的趋势.摩擦力F0=2 N、3 N、4 N工况下的面内一阶加速度时程与频谱图和F0=5 N 工况相似，此处不再赘述.

图7 面内一阶加速度时程与频谱图（l1/L=0.05，F0=5 N）Fig.7 First-order acceleration time-history curve and frequency spectrum（l1/L=0.05，F0=5 N）

4.3 摩擦阻尼器-拉索系统模型强迫振动

本节参考Xu 等［16］研究方法，分析摩擦阻尼器对小幅激振力与大幅激振力时拉索强迫振动共振幅值的减振效果.设置扫频范围1～12 Hz，一阶共振区域扫频速率为0.02 Hz/s，二至五阶共振区域扫频速率为0.04 Hz/s，摩擦阻尼器摩擦力设为2 N.一、三、五阶面内位移由L/2处的激光位移传感器测得，二阶面内位移由L/4处的激光位移传感器测得，四阶面内位移由L/6处的激光位移传感器测得.

激振器产生的激振力设为5 N，得到小幅激振力时，无阻尼器及有阻尼器拉索模型强迫振动面内一阶及五阶振幅-激振频率关系的比较如图8 所示；激振器产生的激振力设为30 N，得到大幅激振力时，无阻尼器及有阻尼器拉索模型强迫振动面内前五阶振幅-激振频率关系的比较如图9 所示.其余各阶结果在表5中列出.

图8 有无阻尼器拉索模型小幅激振时面内振幅-频率关系Fig.8 Small force excited vibration amplitude-frequency relations of cable model with&without friction damper

图9 有无阻尼器拉索模型大幅激振时面内振幅-频率关系Fig.8 Large force excited vibration amplitude-frequency relations of cable model with&without friction damper

在小幅激振力作用下，有阻尼器拉索模型一至五阶强迫振动的共振频率均比无阻尼器拉索模型的自振频率略大.无阻尼器和安装摩擦阻尼器后，一至五阶共振幅值如表5 所示，一至五阶共振幅值分别减小了24.26%、16.79%、9.16%、58.37%、11.46%.在安装摩擦阻尼器后，一至五阶共振频率均有增大的趋势，随着阶数增加，共振频率增大更明显.

在大幅激振力作用下，有阻尼器拉索模型一至五阶强迫振动的共振频率同样比无阻尼器拉索模型的自振频率略大.无阻尼器和安装摩擦阻尼器后，一至五阶共振幅值如表5 所示，一至五阶共振幅值分别减小了53.44%、46.99%、77.33%、82.20%、62.97%，与一、二阶相比，摩擦阻尼器可更加有效地抑制三、四、五阶强迫振动.安装摩擦阻尼器后前五阶共振频率均有增大的趋势，高阶共振频率增大幅度比一阶共振频率增大幅度更大.

综合图8、图9及表5可得结论如下：摩擦阻尼器可以有效减小拉索在小幅与大幅激振力作用下的前五阶共振幅值，并可以更加有效地抑制拉索大幅强迫振动.不论小幅还是大幅强迫振动，安装摩擦阻尼器后，一至五阶的强迫振动共振频率均比自由索模型的自振频率略大.

表5 小幅及大幅激振各阶共振频率及共振振幅Tab.5 Resonant frequencies and resonant amplitude of small and large excitation force

5 结语

通过以上试验及分析可以得出如下结论：

1）摩擦阻尼器用于拉索减振，存在工作与锁住两种工作状态.摩擦阻尼器工作时拉索振幅近似线性衰减，当摩擦阻尼器锁住并停止工作后，由于拉索内阻尼极小，振动衰减极慢.由此可知，系统对数衰减率的最大值与振幅相关，当振幅较小时，摩擦阻尼器不工作，对数衰减率几乎为0；随着振幅逐渐增大，对数衰减率逐渐增大并取得最大值；随着振幅继续增大，对数衰减率又开始逐渐减小.

2）对数衰减率-振幅曲线随着摩擦力的增大向振幅增大的方向平移，其一阶最大对数衰减率基本不变，临界工作振幅及最大对数衰减率对应的振幅逐渐增大，摩擦力越大，对数衰减率-振幅曲线下降段越平缓.

3）摩擦阻尼器-拉索系统在自由衰减振动过程中频率缓慢增大；当摩擦阻尼器由工作状态转换为锁住状态时，系统的自振频率有小幅度突增.

4）摩擦阻尼器可以有效减小不同幅值激振力作用时强迫振动的共振幅值，并且对大幅激振的减振效果更明显.在大幅激振力作用下，摩擦阻尼器可使拉索前五阶共振幅值减小53.44%～82.20%；阶数越高，摩擦阻尼器对共振幅值的减小幅度越大.

摩擦阻尼器在工作时，可以为拉索系统提供较大的阻尼比；当拉索振动幅值比较小时，摩擦阻尼器不工作可以减少阻尼器的磨损.目前摩擦阻尼器在国外实际工程中已得到了一定的推广应用，在国内已应用于万州长江公路三桥.