波浪形斜拉索的气动力及风致振动特性

孙一飞，邵林媛，刘庆宽，2，3†，靖洪淼，2，李震，常幸，王仰雪

（1.石家庄铁道大学土木工程学院，河北石家庄 050043；2.省部共建交通工程结构力学行为与系统安全国家重点实验室（石家庄铁道大学），河北石家庄 050043；3.河北省风工程和风能利用工程技术创新中心，河北石家庄 050043）

交通运输的快速发展、高强材料和先进建造技术的应用，促使大跨度桥梁（悬索桥、斜拉桥和拱桥）的跨度逐步增加，桥梁上索杆结构（主缆、吊索、斜拉索和吊杆）的尺寸也越来越大，风荷载和风致振动问题更加突出.

以苏通长江公路大桥（主跨1 088 m）为例，最长斜拉索达到577 m，在横桥向风作用下，斜拉索上产生的风荷载对于主梁位移及内力的贡献，占到全桥风荷载的60%～70%［1］.对于风致振动，索杆结构经常发生的振动包括风雨振、干索驰振、涡激振动和尾流驰振等.风致振动可能导致索端部接头部分产生疲劳破坏，破坏索的防腐系统，严重时还会造成索的失效.此外，剧烈的振动还会影响行车安全性和行人舒适性，造成经济损失和不良的社会影响.因此，减小索杆结构上的风荷载，抑制甚至消除索杆结构的风致振动具有十分重要的研究意义和工程应用价值.

索杆结构的气动措施包括改变索杆表面状态和截面形状、安装附属结构等，通过改变结构的气动外形，从而改变流动形态和气动特性，进而达到减小阻力和抑制振动的目的.具体的措施主要包括缠绕螺旋线、表面设置凹坑、设置纵向肋条、设置纵向凹槽、变截面索、设置外覆网罩和其他措施.

其中针对变截面索，Bearman 等［2-3］对具有正弦形尾缘或前缘的钝体结构的气动力和旋涡脱落情况进行了研究，结果表明三维波浪外形可改变旋涡脱落方式和减小阻力.Lam 等［4］和Lin 等［5］通过数值模拟方法分别研究了展向呈正弦曲线变化的矩形柱体和翼形柱体的气动力和尾流结构，发现合适尺寸的正弦曲线可以改善矩形柱体的气动力和翼形柱体的失 速 行 为.另 外，Kleissl 等［6］、Ahmed 等［7-8］、Lam等［9-11］、Zhang 等［12］、邹琳等［13］分别针对雷诺数（范围）为5.00×104～3.00×105、5.00×103～2.00×104、1.00×102～2.00×104、5.00×103、3.00×103的情况，通过风洞试验或数值模拟方法研究了各种几何参数的波浪形斜拉索的风压分布、气动力、斯托罗哈数、尾流风速分布、旋涡结构、旋涡形成长度和流动特性等，得出波浪形斜拉索的平均阻力系数和脉动升力系数小于相同直径圆柱的结论.Lam 等［14-15］和Lin 等［16］通过数值模拟的方法研究了低雷诺数下波长和振幅对波浪形斜拉索气动力、斯托罗哈数、风速场、旋涡结构和流动特性的影响规律，发现波浪幅值越大，阻力系数的减小越明显.Hanke 等［17］通过数值模拟和风洞试验的方法研究了弹性支撑的波浪形斜拉索的气动力、涡激振动特性以及旋涡结构.Zhang 等［12］也对线性波浪形索气动力和流动特性等进行了研究，并与正弦波浪形索的相应特性进行了比较.

综上所述，关于波浪形斜拉索的气动力特性、风致振动特性及流场结构已得到一些初步结论.但是，仍存在的问题包括：1）涉及的雷诺数较低，已有研究的雷诺数多在103～104，而斜拉索的实际雷诺数多为105量级，两者的差别不容忽视；2）对风致振动影响的研究多集中在涡激振动方面，很少考虑干索驰振等其他风致振动；3）尚未确定具有较好减阻抑振功能的波浪外形的最优几何参数.针对上述问题，以某一特定尺寸的波浪形斜拉索为研究对象，在1.00×105～3.86×105的雷诺数范围内，通过测力试验、测压试验、涡激振动试验、干索驰振试验，研究波浪形斜拉索的整体气动力、风压分布、局部气动力、涡激振动和干索驰振特性，探索几何参数对气动力和风致振动特性的影响规律.

1 风洞试验设置

风洞试验在石家庄铁道大学风工程研究中心STU-1 风洞进行，低速试验段模型区宽4.4 m，高3.0 m，长24.0 m，最大风速≥30 m/s，湍流度≤0.4%；高速试验段宽2.2 m，高3.0 m，长5.0 m，最大风速≥80 m/s，湍流度≤0.2%.

波浪形斜拉索的几何示意图如图1 所示，Saddle（S）、Middle（M）、Node（N）分别表示最小直径位置、平均直径位置、最大直径位置，几何外形可用式Dz=D-2a·sin（2π/λ·z）来表示，其中，a是波浪的幅值，λ是波浪的波长，D是平均直径，z是距平均直径位置的距离，Dz是z处的直径.

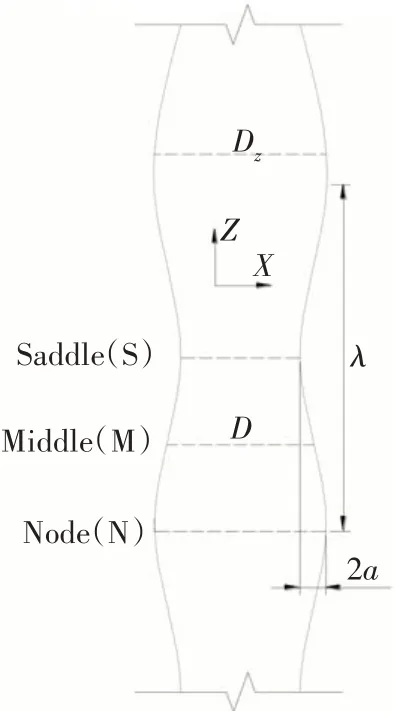
图1 波浪形斜拉索的几何外形示意图Fig.1 Diagram of geometry of the wavy stay cable

斜拉索模型由钢管外覆蒙皮形成，蒙皮为硬质树脂，钢管和蒙皮之间通过系列环向加劲肋连接，模型具有足够的强度和刚度.

斜拉索模型长度为L=1.70 m，平均直径为D=0.12 m，波幅为a=3.60 mm，波长为λ=0.72 m，将a和λ除以D得到无量纲波幅和波长，分别为a/D=0.03 和λ/D=6.00.

为了获得气流经过模型表面时的风压分布，在模型Node 和Saddle 之间均匀布置5 圈测压孔，按所在截面直径从小到大排列，依次命名为S、Q、M、3Q、N，每圈等间距布置36 个测压孔，间隔10°，其展向和环向布置如图2所示.

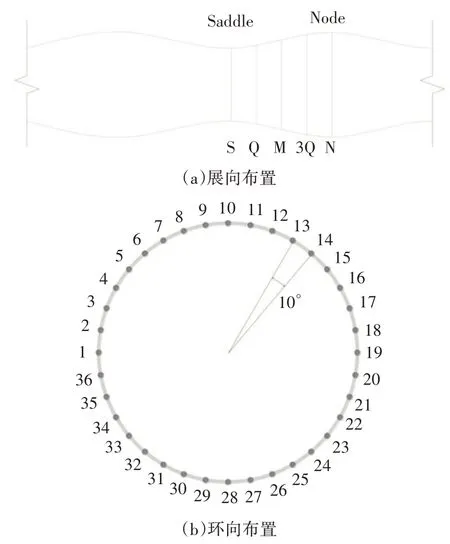
图2 测压孔布置示意图Fig.2 Diagram of pressure taps arrangement

测力试验在高速试验段进行，模型两端安装了圆形端板和补偿模型，以消除端部效应，端板直径是0.60 m（5D）［18］，厚度是0.50 cm，具有足够的刚度，补偿模型的直径为0.12 m（1D），模型通过内置钢管固定到风洞外部的刚性框架上.测压试验的安装设置和测力试验相似，但两端只安装了端板.安装好的测力和测压模型如图3所示.

图3 安装好的测力和测压模型Fig.3 Installed models in aerodynamic forces and surface pressure measurement tests

干索驰振试验在高速试验段进行，使用的模型和端板与静态试验相同.不同之处是，在测振试验中，模型两端分别通过4 根竖向弹簧连接在风洞外部的刚性框架上，模型、端板、连接件、弹簧组成振动系统，质量为m=19.34 kg，刚度K=1.00×104N/m，自振频率f=3.54 Hz，阻尼比ξ=0.30%，斯卡顿数Sc=4πm0ξ/ρD2=22.83，其中，m0是振动系统单位长度的质量，ρ是空气密度，根据试验时风洞内的温度、湿度和压强，算得ρ=1.13 kg/m3.利用2 根大约6 m 长的细钢丝限制模型的顺风向运动，使得振动系统仅发生横风向振动.振动系统自振特性如表1 所示，振动系统安装示意图如图4所示.

图4 干索驰振试验模型系统的安装示意图Fig.4 Schematic diagram of model system in galloping test

表1 振动系统自振特性Tab.1 Natural vibration characteristics of vibration systems

涡激振动试验在低速试验段进行，振动系统设置和干索驰振试验相同，只是两端固定框架不同，自振特性见表1.需要说明的是，涡激振动发生风速低，大约在2～3 m/s；而干索驰振发生风速高，大约在30 m/s 以上，考虑到风洞内风速的稳定性，涡激振动和干索驰振试验分别在低速试验段和高速试验段进行.

在波浪形斜拉索的测力试验、测压试验、干索驰振试验和涡激振动试验中，模型的阻塞率分别为4.64%、4.64%、4.64%和1.55%，均小于5%.雷诺数的变化通过改变风速来实现.

为了比较波浪形斜拉索和标准斜拉索的气动特性，也进行了标准斜拉索的气动力测量、干索驰振和涡激振动试验，标准斜拉索模型的直径与波浪形斜拉索模型的平均直径相同，均为0.12 m，标准斜拉索振动系统的自振特性如表1所示.

2 试验结果分析

2.1 风压分布

2.1.1 标准斜拉索的风压分布

风压系数表示某个局部位置的风压与来流动压的比值，按式（1）计算.

式中：i=1～36，是测压孔编号；Cpi（t）是测压孔i的风压系数时程；pi是测压孔i的压力时程；ps是来流静压；pt是来流总压.将Cpi（t）的平均值定义为平均风压系数，记为Cpi（Cp）.

雷诺数是影响结构绕流形态的一个重要参数，定义如式（2）所示.

式中：Re为雷诺数；U为来流平均风速；Dc为斜拉索模型的特征尺寸，波浪形斜拉索和标准斜拉索分别取Dc=0.112 8 m（最小直径）和Dc=0.12 m；ν为空气的运动黏性系数.

对于标准斜拉索（圆柱）来说，随着雷诺数的增加，周围绕流会经历不同的流态，不同流态从低到高对应的雷诺数区域分别为亚临界区、临界区、超临界区和高超临界区，临界区又包括预临界区（TrBL0）、单分离泡区（TrBL1）和双分离泡区（TrBL2）.由于绕流形式不同，圆柱在不同的流态也展现出不一样的气动力特性和风压分布规律.

提取文献［19］的数据，将标准斜拉索（圆柱）在TrBL0～TrBL2 范围内的平均风压分布结果绘制在图5中，分析标准斜拉索在临界区不同流态下的平均风压分布规律和流动特征.

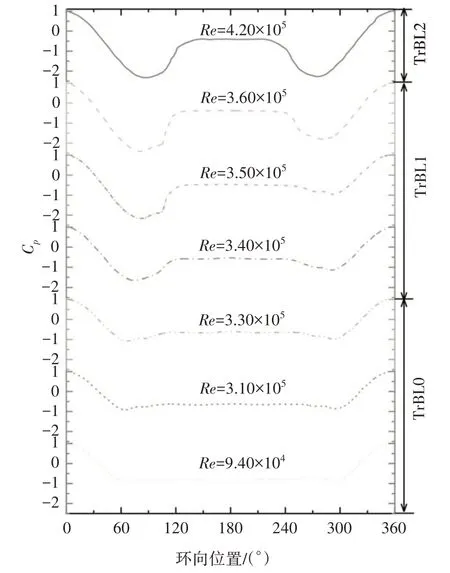
图5 标准斜拉索的平均风压分布Fig.5 Mean pressure distribution of regular stay cables

在Re=9.40×104～3.30×105范围内，对应预临界区（TrBL0），圆柱两侧的平均风压对称分布，在Re=9.40×104时，最小平均风压系数约为-0.97，基本压力系数约为-0.84；随着雷诺数的增加，基本压力系数稍微增加，最小平均风压系数略微减小，且对应的环向角增大，流动分离点后移，尾流宽度变窄.

在Re=3.40×105～3.60×105范围内，对应单分离泡区（TrBL1），圆柱两侧平均风压分布明显不对称，一侧的最小风压区域更突出，这是因为边界层转捩在这一侧率先发生，层流分离后，转捩成湍流，再附到壁面上，形成分离泡，分离点后移，使得该侧压力显著减小；且在该雷诺数范围内，随着雷诺数的增大，最小风压系数继续减小，基本压力系数进一步增大，分离点继续后移，尾流进一步变窄.

当Re=4.20×105时，对应双分离泡区（TrBL2），风压分布又回归到对称状态，另一侧也产生了转捩导致的分离泡，尾流则继续变窄.

2.1.2 波浪形斜拉索的风压分布

针对波浪形斜拉索模型，进行了4 次测压风洞试验，其中包含了风速增大过程和风速减小过程，图6 是Node 处在Re=1.00×105的环向风压分布的4 次试验结果，并同文献［19］和文献［20］分别在Re=9.40×104和Re=1.00×105的结果进行了比较.

由图6 可知，4 次试验得到的平均风压系数曲线吻合良好，且风速增大和风速减小的试验结果一致.同时，试验结果与文献［19］和［20］的圆柱结果相比，曲线形状相似，压力系数大小有所差别.

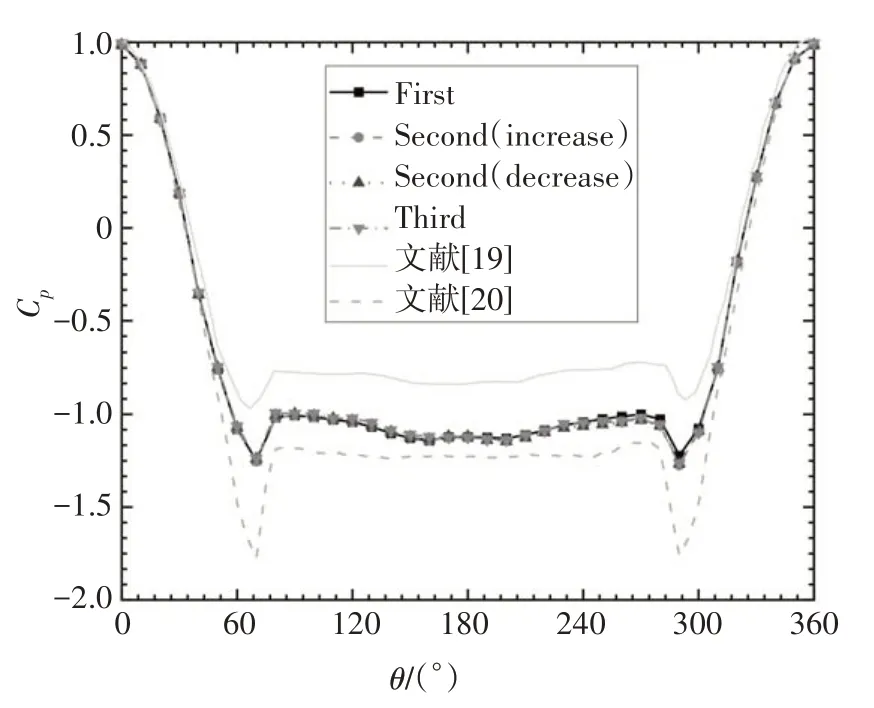
图6 Re=1.00×105时Node处平均风压分布Fig.6 Mean pressure distribution at Node for Re=1.00×105

图7给出了波浪形斜拉索Node处平均风压分布随雷诺数的变化规律.

结合图5、图7，可以得到波浪形斜拉索的平均风压分布规律与标准斜拉索的异同点.

图7 波浪形斜拉索Node处的平均风压分布Fig.7 Mean pressure distribution of wavy stay cable at Node

相同点：随着雷诺数的增加，最小风压系数减小，基压系数增大，分离点后移，尾流宽度变窄.

不同点：波浪形斜拉索的风压分布的非对称性较弱，不如标准斜拉索明显，这说明即使非常微弱的展向截面直径变化也会导致绕流发生明显的变化.

此外，波浪形斜拉索的平均风压分布沿展向是变化的，表现出三维特征.图8 是不同雷诺数下波浪形斜拉索的平均风压分布沿展向的变化规律.

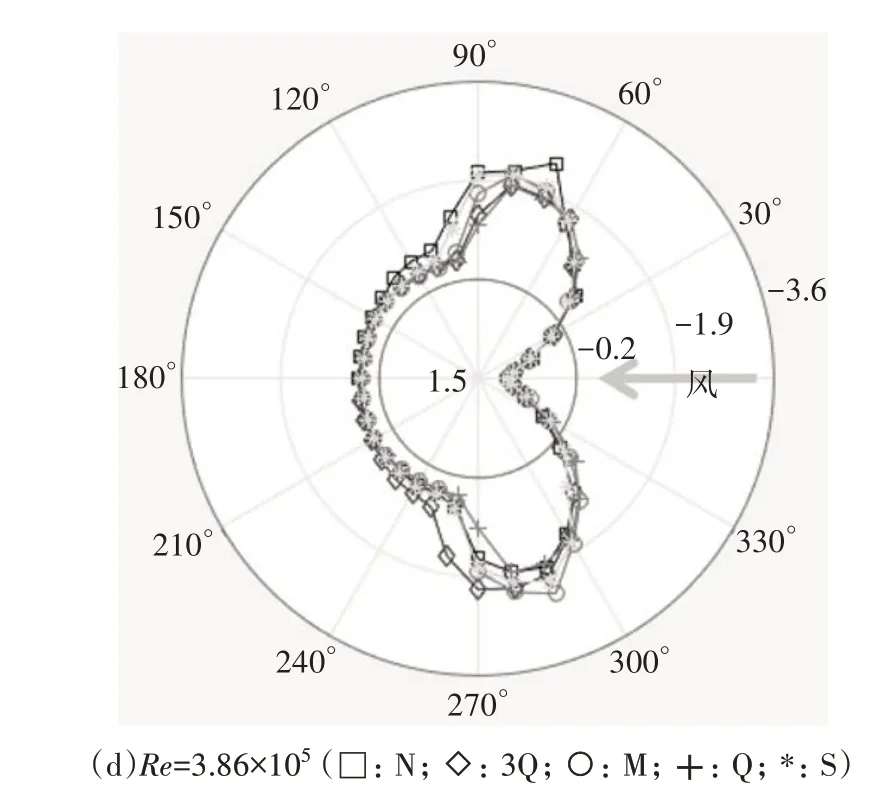
图8 波浪形斜拉索平均风压分布的展向相关性Fig.8 Spanwise correlation of local mean pressure coefficient for wavy stay cable

根据图8 可知：在不同的雷诺数范围内，波浪形斜拉索平均风压分布的展向相关性呈现不同的变化规律.如图8（a）所示，在Re=1.00×105～2.04×105范围内，平均风压分布曲线基本重合，表明平均风压分布沿展向几乎无变化，相关性特别强.

如图8（b）所示，在Re=2.23×105～2.44×105范围内，平均风压分布曲线不再重合，尤其是3Q 处的平均风压曲线明显区别于其他曲线，表明平均风压分布沿展向开始缓慢呈现出不同，相关性开始减弱.

如图8（c）所示，在Re=2.67×105～3.67×105范围内，3Q处平均风压分布曲线非常突出，两侧的风压系数显著减小，且随着雷诺数的增加，其他位置的平均风压分布曲线向3Q处靠拢，但是靠拢速度不尽相同，根据目前的结果，Q 处最快，M 和N 处居中，S 处变化最迟钝，相关性很弱，这是因为该雷诺数区间对应单分离泡区，但是展向各位置出现分离泡的先后不同.

如图8（d）所示，在Re=3.73×105～3.86×105范围内，各位置处的平均风压分布曲线又趋于重合，各位置均进入双分离泡区，相关性较强.

根据上述平均风压系数与雷诺数、展向位置的关系可知，从低雷诺数到高雷诺数，波浪形斜拉索的风压系数也会经历和标准斜拉索（圆柱）相似的变化规律.但是，沿展向，波浪形斜拉索表现出明显的三维特性，不同展向位置的转捩和分离不同，造成不同的流动形式和风压分布，三维特性还会随雷诺数变化.

2.2 气动力

为了直观地对比波浪形斜拉索和标准斜拉索的气动力大小，定义了整体气动力系数和局部气动力系数.

通过测力试验得到模型的整体阻力和升力，将其无量纲化处理得到整体阻力系数和升力系数，如式（3）所示.

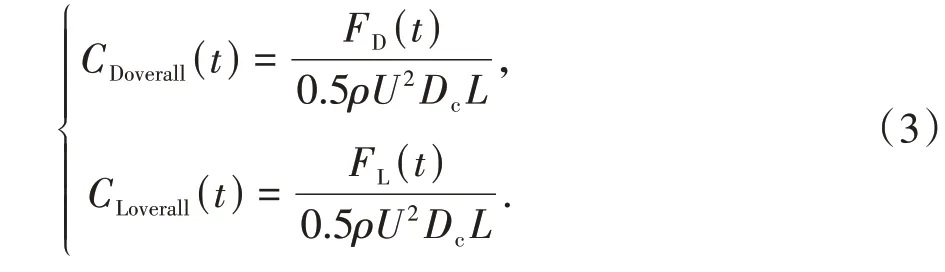
式中：CDoverall（t）和CLoverall（t）分别是整体阻力系数和升力系数时程；FD（t）和FL（t）分别是整体阻力和升力时程.将CDoverall（t）、CLoverall（t）、FD（t）和FL（t）的平均值分别定义为整体平均阻力系数、整体平均升力系数、整体平均阻力和整体平均升力，记为CDoverall、CLoverall、FD和FL.

通过测压试验得到所有测压孔的压力，将展向各位置的环向风压进行积分，得到展向各位置的局部气动力，然后无量纲化得到局部气动力系数，如式（4）所示.需要说明的是，局部气动力系数是基于展向各位置的截面直径Dz的.

式中：CD（t）和CL（t）分别是局部阻力系数和升力系数时程；n=36 为测压孔数量；θi是测压孔i的法向与来流方向的夹角；li是测压孔i代表的弧长.将CD（t）和CL（t）的平均值定义为局部平均阻力系数和平均升力系数，记为CD和CL.

图9 给出了波浪形斜拉索的整体平均阻力系数和升力系数以及展向各位置的局部平均阻力系数和升力系数，为方便对比，列出了当前研究和文献［21］关于标准斜拉索的整体平均气动力系数.

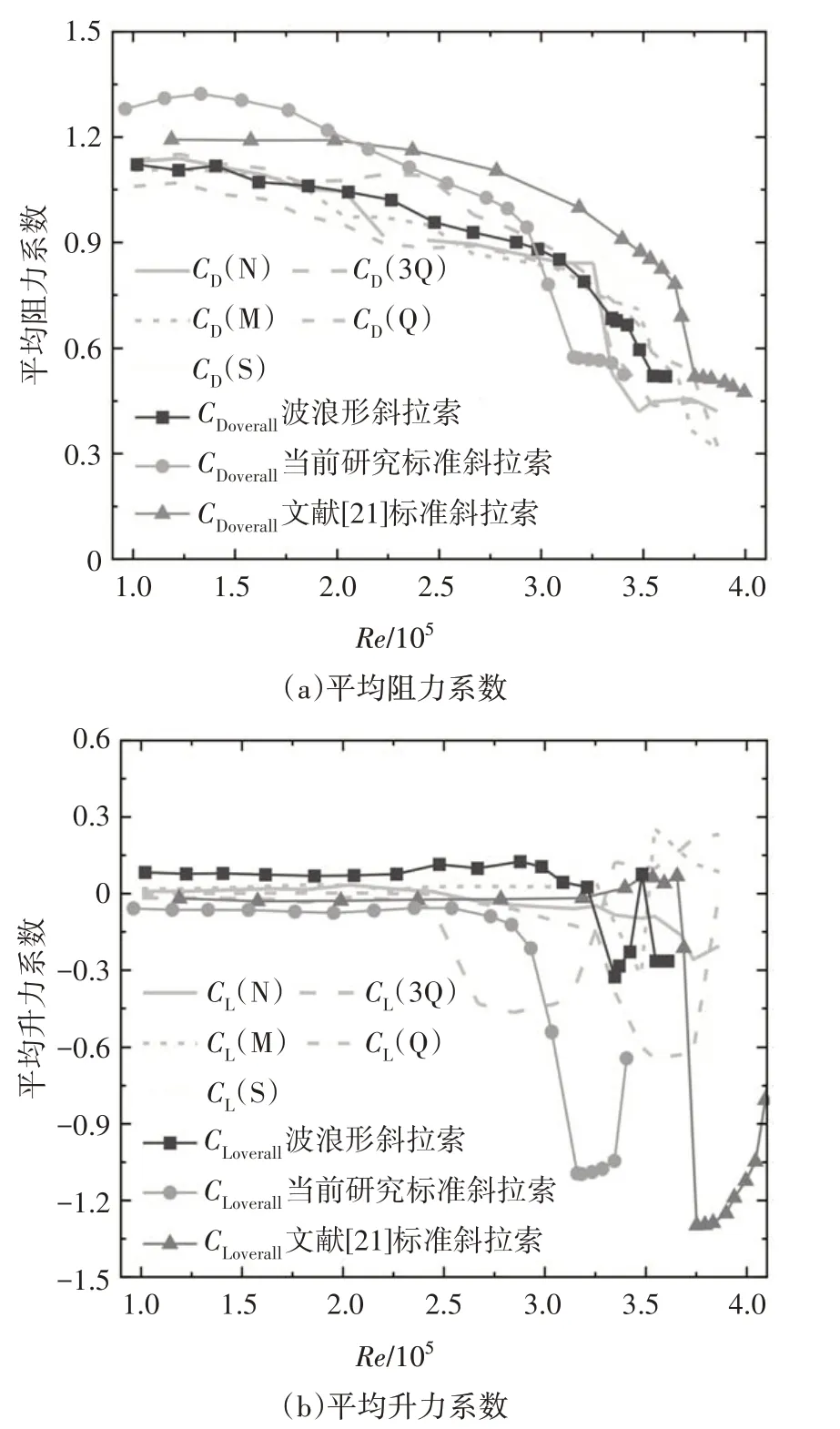
图9 波浪形斜拉索的平均气动力系数Fig.9 Mean aerodynamic coefficients of wavy stay cable

根据图9（a）可得，就总体趋势而言，无论是整体还是局部平均阻力系数，波浪形斜拉索的平均阻力系数随雷诺数的变化规律，和标准斜拉索的结果相似，均表现为随着雷诺数增大而减小，与平均风压分布随雷诺数的变化规律一致.虽然当前研究和文献［21］关于标准斜拉索的结果存在一定差异，但仍然可以观察到：在Re=1.10×105～3.35×105范围内，波浪形斜拉索的平均阻力系数小于标准斜拉索的结果，例如，当Re≈1.20×105时，当前研究和文献［21］的标准斜拉索整体平均阻力系数分别为1.31 和1.19，波浪形斜拉索的整体和局部（N-S）的平均阻力系数分别为1.11、1.14、1.15、1.11、1.07 和1.10，最大减小率为18%；当Re≥3.35×105时，当前研究和文献［21］的标准斜拉索以及波浪形斜拉索的平均阻力系数曲线急剧下降先后不同，按总体规律说，波浪形斜拉索的平均阻力系数大于当前研究的标准斜拉索结果，但小于文献［21］的标准斜拉索相应结果，例如，Re≈3.40 × 105时，当前研究和文献［21］关于标准斜拉索整体平均阻力系数分别为0.53 和0.91，波浪形斜拉索的整体和局部（N-S）的平均阻力系数分别为0.67、0.42、0.50、0.71、0.67 和0.79.结果表明波浪形斜拉索具有一定的减阻能力，尤其是在低雷诺数范围内.

根据图9（b）可得，就总体趋势而言，波浪形斜拉索的平均升力系数随雷诺数的变化趋势和标准斜拉索相似，即在低雷诺数时没有平均升力，随着雷诺数增大，出现了显著的平均升力，雷诺数继续增大，平均升力减小直至消失，符合前述的平均风压分布对称性规律.但是，波浪形斜拉索的最大平均升力系数小于标准斜拉索的结果，在试验雷诺数范围内，当前研究和文献［21］的标准斜拉索整体最大平均升力系数分别为-1.09 和-1.30，波浪形斜拉索的整体和局部（N-S）的相应结果分别为-0.33、-0.26、-0.47、-0.32、-0.65和-0.82，最大减小率为80%.

为了进一步揭示波浪形斜拉索的减阻情况，图10直接对比了波浪形斜拉索和标准斜拉索的总体气动力，包括平均阻力FD、平均升力FL和0.5ρU2DcL.

由图10（a）可得，在Re=1.10×105～3.35×105范围内，标准斜拉索的平均阻力显著大于波浪形斜拉索，而当Re≥3.35×105时，标准斜拉索的平均阻力小于波浪形斜拉索，与平均阻力系数的结果一致.至于平均升力，根据图10（b）可得，标准斜拉索的最大平均升力为249 N，而波浪形斜拉索则是67 N，差距明显.根据图10（c）可得，两种模型的0.5ρU2DcL相差很小，这表明如此微小的面积差异不会导致显著的气动力变化，也从侧面证明两种模型之间FD、FL、CD、CL的差别主要是由气动外形改变导致的绕流变化，而非面积的差异所致.

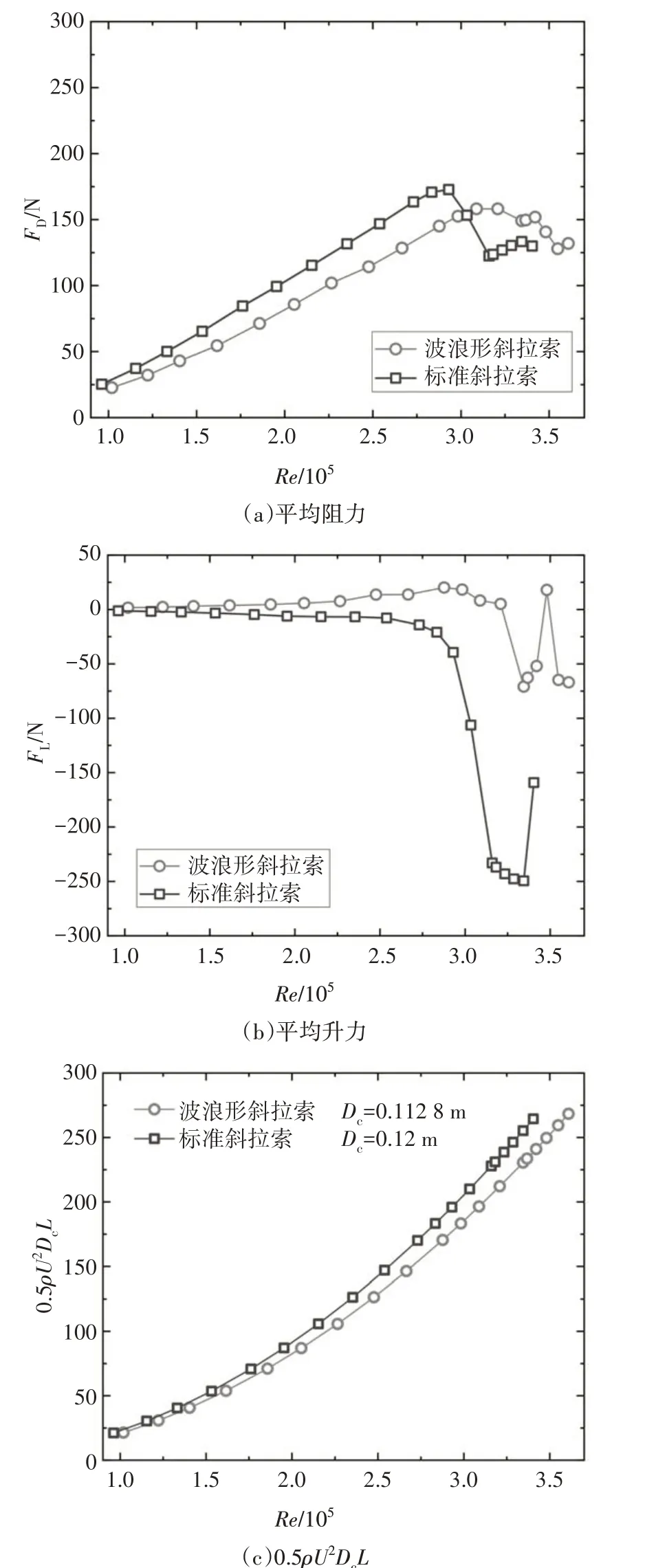
图10 波浪形斜拉索和标准斜拉索气动力比较Fig.10 Comparison of aerodynamic forces between the wavy and regular stay cable

图11 给出了任意两个展向位置升力系数的相关系数，相关系数根据式（5）计算.

式中：CLj和CLk表示任意两个展向位置的升力系数时程；cov表示协方差；σ表示标准差；ρ表示相关系数.

根据图11 可知，不同雷诺数下任意两个展向位置升力系数之间的相关情况，相当于风压分布对称性沿展向的定量变化.随着雷诺数从低到高，升力系数的展向相关性呈现出四种不同的变化规律.

图11 波浪形斜拉索升力系数的展向相关性Fig.11 Spanwise correlation of CL（t）of wavy stay cable

第一，如图11（a）所示，在Re=1.00×105～1.82×105范围内，N 和3Q 处强相关，M 和N、3Q、S 中等程度相关，S、Q与其他位置的相关性整体较弱.

第二，如图11（b）所示，在Re=2.04×105～3.26×105范围内，相比于前一个雷诺数范围，展向相关性显著降低，仅N 和3Q、M 相关性相对较强，整体上均较弱.

第三，如图11（c）所示，在Re=3.35×105～3.73×105范围内，相比于前一个雷诺数范围，展向相关性继续降低，仅N和3Q的相关性相对较强，且为负相关.

第四，如图11（d）所示，当Re=3.87×105时，N 和3Q 的相关系数从负值变为正值，量值不变，展向相关性整体较弱.

2.3 涡激振动

斜拉索在风的作用下可能发生涡激振动，从而造成结构的疲劳破坏［22］.图12 是波浪形斜拉索与标准斜拉索的涡激振动无量纲振幅A/Dc（A为振动位移时程的根方差）随约化风速U/fDc的变化规律.

图12 波浪形斜拉索与标准斜拉索涡激振动特性对比Fig.12 Comparison of VIV characteristics of wavy and regular stay cable

由图12 可知，标准斜拉索的涡激振动发生在U/fDc=5.00～6.48 范围内，对应锁定区，最大无量纲振幅约为A/Dc=0.053，对应的约化风速为5.85；对于波浪形斜拉索而言，锁定区范围为U/fDc=5.24～7.83，锁定区间有所变宽，但最大振幅为A/Dc=0.035，比标准斜拉索的相应结果减小了34%，

其对应的约化风速为6.94，比标准斜拉索提高了约16%.上述结果表明，波浪形斜拉索对涡激振动具有一定的抑制作用.

2.4 干索驰振

除涡激振动，干索驰振也是斜拉索经常发生的风致振动［23］，特点是发生风速高、振幅大、危害严重.

图13、图14 分别给出了标准斜拉索和波浪形斜拉索干索驰振的平衡位置和振幅随约化风速的变化规律.其中，A/Dc是无量纲振幅，用“●”表示；C/Dc是无量纲平衡位置（C为振动位移时程的平均值），用“□”来表示；在干索驰振振动过程中，可能出现平衡位置的跳跃，这是两种稳定的振动状态的中间发展过程，相当于，在同一风速下的振动时程曲线中，会出现两个完全不同的平衡位置，这里称为过渡点，用“◇”来表示.

图13 标准斜拉索的干索驰振特性Fig.13 Dry galloping characteristics of regular stay cable

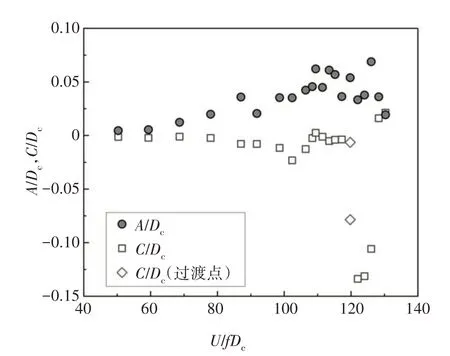
图14 波浪形斜拉索的干索驰振特性Fig.14 Dry galloping characteristics of wavy stay cable

由图13 可知，在U/fDc<110 时，标准斜拉索的振幅随着约化风速的增大呈缓慢增大趋势；当U/fDc>110时，驰振振幅急剧增大，迅速达到最大值，最大值为A/Dc=0.073，但很快衰减.至于平衡位置，当U/fDc<102 时，平衡位置维持在0 附近；当U/fDc=102 时，平衡位置C/Dc从0 快速偏移到0.1；当U/fDc=108～110时，平衡位置C/Dc从0.1 迅速偏移到0.23；当U/fDc=112 时，平衡位置C/Dc往相反方向，即向初始平衡位置快速偏移，C/Dc从0.23 掉落到0.16；随着约化风速进一步增加，当U/fDc=121 时，C/Dc从0.16掉落到0.03；在U/fDc=102～108、110～112、112～121 三个风速范围内，C/Dc基本保持不变，对应稳定的振动过程.

由图14 可知，与标准斜拉索不同，在U/fDc<108时，波浪形斜拉索的振幅随约化风速增加而增大，增大趋势更明显，在低风速下驰振更显著；当U/fDc>108 时，驰振振幅在A/Dc≈0.05 的小范围内波动，相对稳定，最大振幅为A/Dc=0.069.对于平衡位置来说，波浪形斜拉索的平衡位置随约化风速的变化规律与标准斜拉索存在异同点，相同点：第一，较大的平衡位置出现在某一小段风速范围内；第二，在某一风速下，会出现平衡位置随时间的偏移现象，即两种稳定状态的过渡点.不同点：波浪形斜拉索较大的平衡位置对应的风速范围更窄，最大平衡位置的偏移量值也不同，此处，C/Dc最大值约为0.13.

由上可得：波浪形斜拉索的无量纲振幅和平衡位置最大值分别比标准斜拉索小5%和43%，具有一定的抑振性能，但同时波浪形斜拉索发生干索驰振的风速区间更宽，起始风速变低，因此，需要综合考虑实际工程的结构参数和风场参数，有条件地采用波浪形斜拉索来抑制干索驰振.

3 结论

针对某一特定尺寸的波浪形斜拉索，进行了测力试验、测压试验、涡激振动试验和干索驰振试验，得到的主要结论如下：

1）波浪形斜拉索环向平均风压分布随雷诺数的变化规律与标准斜拉索相似，但展向相关性更弱.

2）波浪形斜拉索的平均阻力系数总体而言小于标准斜拉索，在低雷诺数范围可减阻18%，最大平均升力系数相比标准斜拉索可降低80%，具有良好的气动力性能.

3）波浪形斜拉索的涡激振动明显弱于标准斜拉索，最大振幅及其对应的约化风速分别降低了约34%和提高了约16%，抑制涡激振动效果显著.

4）波浪形斜拉索的干索驰振振幅和平衡位置比标准斜拉索分别减小5%和43%，但发生振动的风速范围变宽，需要综合考虑实际工程的结构参数和风场参数，有条件地采用波浪形斜拉索来抑制干索驰振.