被动负刚度装置与线性滞回阻尼器组合对斜拉索多模态振动的阻尼效果

孙利民，孙浚杰，狄方殿，邹易清，王萌，陈林†

（1.同济大学桥梁工程系，上海 200092；2.土木工程防灾国家重点实验室（同济大学），上海 200092；3.柳州欧维姆机械股份有限公司，广西柳州 545006；4.城市与工程安全减灾教育部重点实验室（北京工业大学），北京 100124）

斜拉索是斜拉桥最为关键的受力构件之一，但很容易出现异常振动［1］.因此，斜拉索振动与控制问题受到了广泛关注［2］.例如，在运营期的风、雨和车辆等作用下，其常出现明显甚至是大幅振动［3-4］，严重威胁着桥梁的适用性和安全性［5］.

为有效控制斜拉索振动，工程中常在索端安装阻尼器增加索的模态阻尼［6］.现有研究表明，阻尼器的固有刚度会减小斜拉索振动过程中阻尼器的相对变形，削弱对索的阻尼效果［5］.相反，通过主动、半主动或被动控制方法实现的负刚度能够增加阻尼器位置处的斜拉索位移，从而提高阻尼效果.Høgsberg等［6］在结构振动控制中考虑了具有负刚度系数和可采用分数阶导数模型描述的阻尼器，表明该阻尼器可提供相位超前的阻尼力；还发现由于安装阻尼器而增加的质量同样能增大位移，从而增强阻尼效果.

近年来，基于惯性质量和负刚度机理的减振效果提升手段是结构减振抗震研究的热点.基于惯容器的结构振动控制研究可追溯到Ikago 等［7］和Lazar等［8］.后续研究考虑了不同惯容器、弹簧和阻尼器组合的动力性能［9-10］、振控效果［11-12］和基础隔震性能［13-14］等.Lazar 等［15］、Sun 等［16］、Lu 等［17］较早在斜拉索-阻尼器系统中引入惯容器，引起了该领域学者的关注［18-22］.进一步研究中关注了具有惯性质量效果的阻尼器的研发，如陈政清等［23］、孙洪鑫等［24］、李亚敏等［25］采用电磁技术同时实现惯性力和阻尼力，并采用实索试验进行了验证［26］.

结构振动控制中关于负刚度现象的研究可追溯到Iemura 等［27-28］.早期学者们从摩擦、半主动或主动控制装置的力-位移滞回曲线中观察到减振装置的负刚度行为，称其为表观负刚度或伪负刚度（PNS）.随后，发展了基于PNS 的半主动和主动控制算法，相关研究包括Iemura 等［29］、Li 等［30］、Ou 等［31］、Høgs⁃berg［32］、Weber等［33］.2013年，Sarlis 等［34］、Pasala 等［35］研发了基于预压缩弹簧的被动负刚度装置（NSD），并开展了试验验证.针对斜拉索减振，Chen 等［36］将NSD 与黏滞阻尼器结合，突破了传统阻尼器对斜拉索附加阻尼的限制.Zhou 等［37］进一步开展了附加NSD 和黏滞阻尼器的斜拉索的模型试验，验证了NSD 结合阻尼器可作为斜拉索半主动或主动拉索控制的经济有效的替代方案［38-39］.

斜拉索减振实践中常见的阻尼器，例如高阻尼橡胶阻尼器［40］和黏性剪切阻尼器［6］，均可用线性滞回阻尼模型描述其力学行为.即将此类阻尼器建模为一个具有复刚度和损耗因子的弹簧.现有研究已量化了其对斜拉索的阻尼效果［41-42］，亦分析了在斜拉索上同时安装多个线性滞回阻尼器以及与其他阻尼器组合时的优化设计［43-45］.线性滞回阻尼器可为拉索各阶模态提供几乎相等的阻尼，但与黏滞阻尼器相比，其最优附加阻尼受到自身刚度效应的限制，导致阻尼效果偏低.因此，本文提出利用负刚度装置提升线性滞回阻尼器对斜拉索的阻尼效果.NSD 可与阻尼器在新桥建设时在同一位置安装，亦可以在斜拉索减振系统维护升级时安装.因此将考虑NSD与阻尼器分别在索端部任意位置安装的情况，通过理论研究和实际设计案例，讨论NSD 的效果和可行性.

1 斜拉索阻尼器系统复频率方程

本节首先建立斜拉索阻尼器系统的动力方程，然后采用复数模态分析方法得到系统的复频率方程，进而建立系统复频率方程数值求解方法.

1.1 系统动力方程

图1 为一根斜拉索上安装NSD 和线性滞回阻尼器进行组合减振的示意图.斜拉索通过变换后水平放置，以弦线为x轴，其弦长为L，水平张力为T，拉索单位长度质量为m，轴向刚度为EA，对于长索，其抗弯刚度和拉索自身阻尼可忽略不计［46］.图1 中，k1为NSD 的刚度系数，k2为线性滞回阻尼器的刚度系数，φ为损耗因子.y(x)和v(x，t)分别表示斜拉索在重力下的变形和动位移.

图1 斜拉索-NSD-阻尼器系统模型Fig.1 A shallow cable equipped with an NSD and a damper

对于斜拉索，其静止状态的形状可假定为抛物线函数：

其中θ为拉索倾角，Le≈[1+8(d/L)2]L.

斜拉索-NSD-线性滞回阻尼器系统的复频率特征方程由式（2）系数矩阵S的行列式等于0获得.

1.2 系统频率方程

定义量纲归一化参数如下：

频率方程可以写成如下的形式：

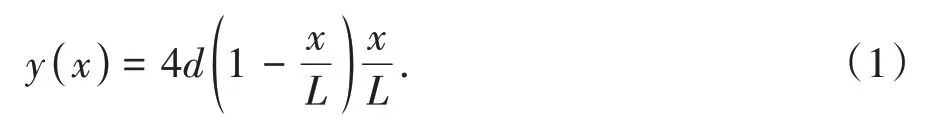
式中：d为拉索跨中的垂度.

将NSD记做装置Ⅰ，线性滞回阻尼器为装置Ⅱ，斜拉索被二者分为3 个索节段.为了推导方便，如图1所示，连接点用Pp编号，p=0，1，2，3.P0和P3分别表示斜拉索的左、右锚固点，P1和P2为NSD 和阻尼器的安装位置.lp表示第p个拉索单元的长度（Pp-1和Pp点间的水平距离）.

根据文献［47］中的方法，得到如下方程：

式中：为索安装阻尼器后第n阶振动的量纲归一化圆频率.当忽略斜拉索垂度时，特征方程可化简为：

上述非线性方程可以采用常用的数值方法例如牛顿法求解，采用无阻尼器安装时的解作为初值进行迭代直至达到设定精度.求解得到复数频率之后，阻尼按式（5）得到.

式中：imag(·)表示求复数的 虚部；|·|表示取复数的模.

2 多模态阻尼效果

基于上节中的系统阻尼求解方法，研究NSD 和线性滞回阻尼器对斜拉索的多模态阻尼效果.考虑到垂度参数主要影响索的一阶阻尼［22］，而对其他振动模态的阻尼影响很小，此处主要采用张紧弦模型以简化计算.在进行多模态阻尼分析时，定义为第i至第j阶模态的最优阻尼，即第i至第j阶模态阻尼均不小于；同时，达到时的最优线性滞回阻尼器刚度系数表示为.

2.1 NSD刚度系数的影响

图2 所示为不同NSD 刚度系数情况下，斜拉索一阶、二阶模态阻尼比随阻尼器刚度系数的变化曲线.图2 中结果对应斜拉索的张紧弦模型，NSD 与线性滞回阻尼器安装在同一位置，即=0.03、=0.97，固定阻尼器的损耗因子为φ=0.7.NSD 的刚度系数分别为0、-5、-10 和-15.由图2 可见，线性滞回阻尼器对斜拉索振动的各阶效果几乎一致，NSD 对各阶阻尼的提升效果也相同.图中实心圆圈标注了各工况下，最优阻尼和对应的阻尼器刚度系数，即.可见，NSD 的负刚度系数绝对值越大，可达到的最优阻尼越大，对应最优的阻尼器刚度系数越小.

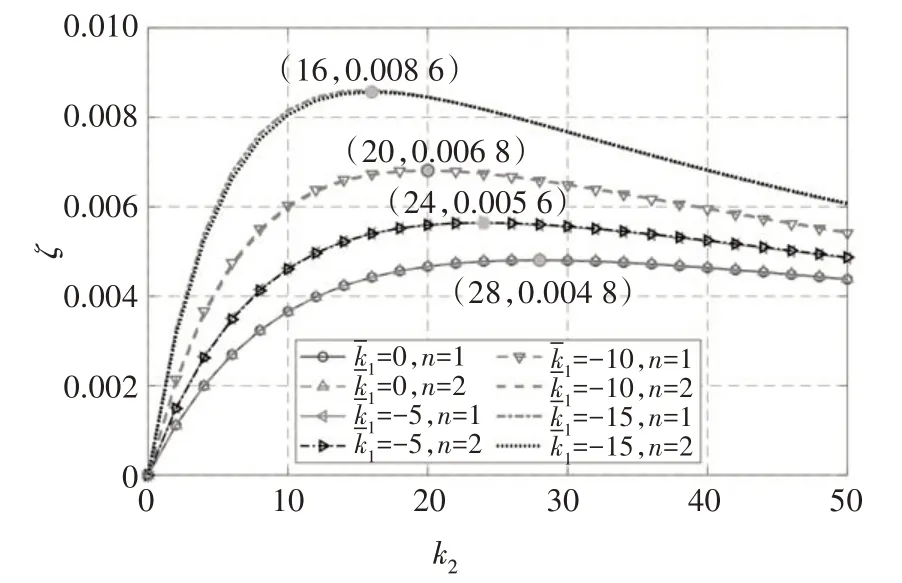
图2 不同NSD刚度系数时斜拉索阻尼随阻尼器刚度系数的变化曲线Fig.2 Damping curves of the stay cable with respect to damper stiffness coefficient for different NSD coefficients

2.2 安装位置的影响

考虑在斜拉索减振系统维护升级中，NSD 可能有线性滞回阻尼器同端或异端两种布置方式.根据图1 的符号设定，同端布置对应较大的，异端布置时较小.

2.2.1 同端安装

图3 所示为NSD 与阻尼器同端安装且位于阻尼器和索锚固点之间时，斜拉索前五阶模态最优阻尼比（见图3（a））和对应的最优阻尼系数（见图3（b））随NSD 位置的变化曲线.其中，NSD 的刚度系数为=-5，同时考虑了阻尼器安装在2%、3%、4%和5%索长的情况.

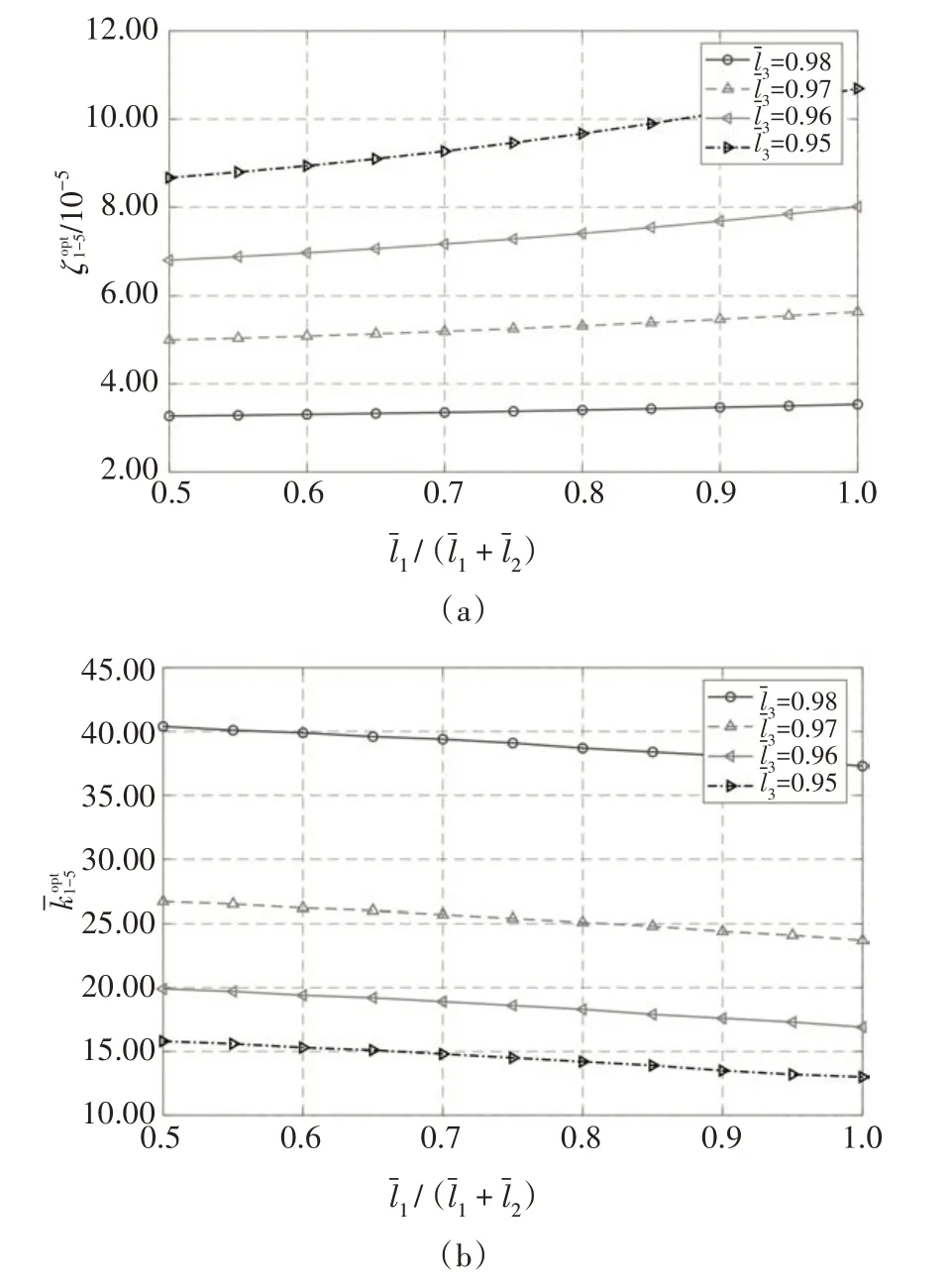
图3 NSD与阻尼器同端布置时斜拉索多模态最优阻尼及对应的最优阻尼器刚度系数随NSD安装位置的变化Fig.3 Variations of optimal multimode damping and corresponding damper stiffness coefficient with respect to NSD location when the NSD and damper are close to the same end

从图3（a）可以看到，同端安装情况下，随着阻尼器安装位置远离索锚固点，其最优阻尼逐渐增加，与现有研究结论一致.同样，随着NSD向线性滞回阻尼器的靠近，即趋近于1，最优阻尼比单调增加，即随着NSD增大，斜拉索在阻尼器位置处的相对位移的效果得到增强.由图3（b）可见，阻尼器距跨中位置和NSD越近，阻尼器的最优刚度系数越小.

2.2.2 异端安装

1.湿热下注，气血壅滞。治法：解毒软坚，活血消痈。方名：加味活血消痈汤。组成：夏枯草30 g，紫草30 g，丹皮25 g，红花25 g，桃仁30 g，泽兰叶25 g，三棱25 g，莪术25 g，赤芍30 g，白芍30 g，木通25 g，小茴香25 g。

图4 所示为NSD 和阻尼器分别位于斜拉索两端时，前五阶模态阻尼比及对应的阻尼器最优刚度系数随NSD 和阻尼器安装位置的变化曲线.其中，NSD的负刚度系数=-5，考虑阻尼器安装在2%、3%、4%和5%索长的情况.可见，当NSD 与阻尼器距离很大时，其增强效应几乎为零，因为并没有增加阻尼器位置的振动位移.

图4 NSD与阻尼器异端布置时斜拉索多模态最优阻尼及对应的最优阻尼器刚度系数随NSD安装位置的变化Fig.4 Variations of optimal multimode damping and corresponding damper stiffness coefficient with respect to NSD location when the NSD and damper are close to different cable ends

2.3 损耗因子的影响

对于线性滞回阻尼器，损耗因子是一个重要的性能参数，图5 展示了损耗因子的影响.根据上一节结论，NSD 仅在同端安装的情况下有较好效果，因此取l3=0.97，一致地取=-5.可见，其损耗因子越大，所能实现的最优阻尼越大，并且相应的最优刚度系数越小，不同影响因子情况下，NSD 对其提升效果相近.

图5 斜拉索多模态最优阻尼及对应阻尼器刚度系数随损耗因子的变化曲线Fig.5 Optimal multimode damping and corresponding damper stiffness coefficient of the cable with respect to damper loss factor

3 案例分析

进一步基于实际工程中的斜拉索，讨论NSD 结合线性滞回阻尼器的可行性.以主跨1 088 m 的苏通长江大桥安装有黏性剪切型阻尼器的SJ18U 索为例，斜拉索位置见图6，参数列入表1.

表1 苏通大桥SJ18U斜拉索参数列表Tab.1 Parameters of SJ18U cable of the Sutong Bridge

图6 苏通大桥SJ18U斜拉索布置图Fig.6 SJ18U cable of the Sutong Bridge

为抑制该斜拉索振动，该索采用了常见的黏性剪切型阻尼器，相关研究［5］进行了阻尼器性能和实桥阻尼效果试验.试验结果表明，黏性剪切型阻尼器对拉索多模态阻尼效果相近，可以考虑为线性滞回阻尼器.根据斜拉索-线性滞回阻尼器模型（本文模型在NSD 系数为零的情况）和实测的多模态阻尼值进行拟合估计，得到该阻尼器采用线性滞回模型描述时的参数为k=385 kN/m，φ=0.75，对应的拟合阻尼器的理论阻尼效果列入表2.

表2 采用线性滞回阻尼模型模拟苏通大桥SJ18U斜拉索黏性剪切阻尼器的效果Tab.2 Damping effects of SJ18U cable attached with the viscous shear damper by using the linear hysteretic damping model for the damper

由表2 可见，线性滞回模型的模拟结果良好，绝大部分模态误差均在5%上下，最大误差为10%.以下基于上述拟合参数设计NSD.如表3 所示，考虑增加的NSD 的量纲归一化刚度系数分别为-5 和-10，NSD 在阻尼器与锚固点间的中点和阻尼器位置安装，对应的NSD参数亦列入该表.

表3 苏通大桥SJ18U斜拉索采用NSD提升黏性剪切阻尼器减振效果设计工况Tab.3 Design cases of using NSD for improving damping effect of the viscous shear damper on SJ18U cable of the Sutong Bridge

基于类似的机理，线性滞回阻尼器并联惯容器同样能提高其对斜拉索的阻尼效果［22］.当阻尼器并联一个惯性质量为bp的惯容器后，惯容器对斜拉索第n阶模态将产生的等效负刚度.在此，基于表3 中设计工况3，设计惯容器使其分别针对索第1阶、第4 阶振动产生与工况3 相同的等效负刚度.获得的惯容器的参数列入表4，记作工况4和5，其中为线性滞回阻尼器与并联惯容器位置为量纲归一化并联惯性质量.

表4 苏通大桥SJ18U斜拉索采用并联惯容器提升黏性剪切阻尼器减振效果设计工况Tab.4 Design cases of using inerters for improving damping effect of the viscous shear damper on SJ18U cable of the Sutong Bridge

对比表5 工况3 和工况4、工况5，即分别采用NSD 与惯容器对斜拉索阻尼器效果进行提升，可见，对于确定惯性质量系数时考虑的振动模态，安装NSD 和惯容器后，阻尼器对该阶模态的阻尼效果一致.对于其他模态，惯容器产生的等效负刚度效应在低阶时较小、高阶时较大.过大的负刚度与阻尼器结合反而会在索高阶振动时锁定阻尼器，降低高阶模态阻尼比.对比而言，NSD 相比惯容器在与线性滞回阻尼器组合后对斜拉索的多模态宽频段减振中具有优势.

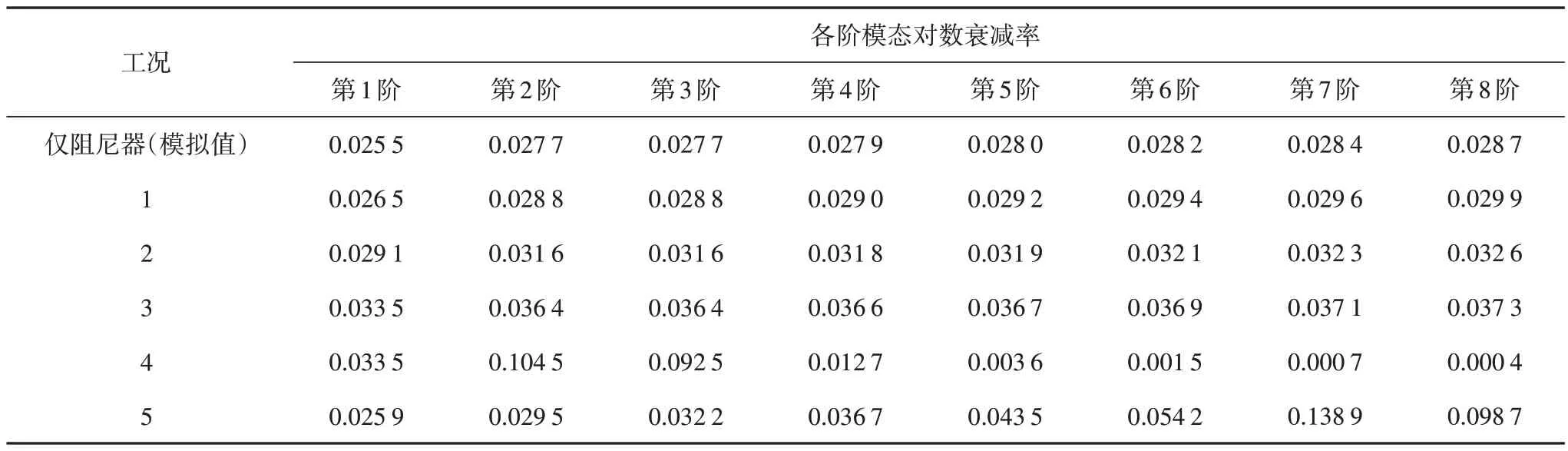
表5 各设计工况中斜拉索多模态阻尼效果对比Tab.5 Comparison of multimode damping of SJ18U cable when using NSD or inerter combined with the viscous shear damper

4 结论

本文提出了结合负刚度装置与线性滞回阻尼器实现拉索多模态振动阻尼提升的方案，通过理论研究和实桥斜拉索案例分析得到如下结论：

1）NSD 结合线性滞回阻尼器能实现斜拉索多阶模态阻尼比的同步提升.

2）NSD 的负刚度系数一定时，其安装位置越靠近阻尼器，可实现的多模态最优阻尼越高.

3）NSD 相比于惯容器对斜拉索-阻尼器系统的多模态阻尼的均衡提升效果更好.

4）对于实际工程中的斜拉索，采用预压缩弹簧结合杠杆放大机制即可满足NSD设计需求.