提篮式系杆拱桥吊索无应力下料长度计算分析

■魏初材

（1.福建省建筑科学研究院有限责任公司，福州 350108;2.福建省绿色建筑技术重点实验室，福州 350108）

在吊杆拱桥施工中，连接拱桥主梁与拱肋之间的吊索（或叫吊杆），如果吊索下料长度过长，则会导致吊索无法张拉到设计索力，甚至锚固端已经到达最大调节量却还未受力的情况；如果吊索下料长度过短，又会导致吊索张拉端锚头有效锚固长度不足，甚至出现无法拧上锚固螺母的情况[1-5]。 吊索一般采用成品索， 在现场不能进行接长或者切割，如果下料长度不准确，只能返厂加工，严重耽误工程进度，因此吊索的无应力精确下料长度至关重要。

吊索的无应力下料长度常用的计算方法通常为根据成桥状态下有应力索长， 通过材料力学公式——胡克定律算出吊索弹性伸长量，再把有应力索长减去弹性伸长量即可得到无应力下料长度[6-8]。此方法为吊索无应力长度理论计算方法，在实际工程运用过程中未考虑施工过程的主梁、 拱肋的制造、安装误差及预拱度(本文称为“建造过程偏差”），导致吊索无应力下料长度出现偏差。 因此，有必要考虑建造过程偏差对理论计算的无应力索长进行修正。

1 吊索无应力长度修正计算

1.1 理论无应力索长计算方法

成桥状态下，拱肋线形、主梁线形及吊索内力为已知，计算吊索无应力长度的方法如下：

假设吊索上端为i，下端为j，通过拱轴线形及主梁线形可求得吊索上端坐标（xi, yi, zi）及下端坐标（xj, yj, zj），通过吊索上下段坐标可求得吊索成桥状态下有应力长度L

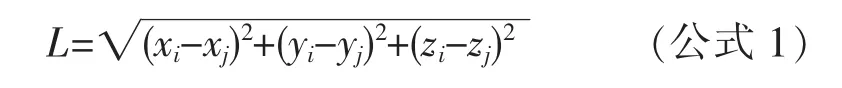
为求得吊索无应力下料长度，主要考虑3 个方面：一是吊索在成桥索力作用下的弹性伸长量Δl1；二是吊索受自重作用下的伸长量Δl2； 三是吊索在自重作用下的垂度引起的伸长量Δl3。

（1）根据材料力学公式，可求得吊索成桥索力作用下的弹性伸长量Δl1：

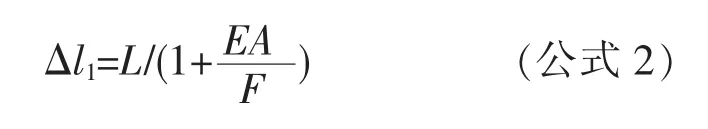
式中，L 为吊索有应力长度；F 为成桥阶段吊索索力；E 为吊索弹性模量；A 为吊索截面面积。

（2）吊索在自重作用下的伸长量Δl2可由下式计算：

式中，w 为吊索单位长度质量。

（3）需要注意的是，提篮系杆拱桥吊索并非垂直布置， 吊索为垂直方向向内倾斜一定的角度，吊索受自重作用下存在垂度， 由垂度引起的伸长量Δl3如下式计算：

式中，q 为吊索自重集度，α 为吊索与水平面夹角。

通过推导可以得到系杆拱桥理论吊索无应力长度计算公式：

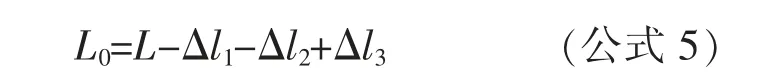
1.2 考虑偏差的无应力索长修正计算方法

由已知的成桥状态（主梁线形确定、拱肋线形确定、吊索索力确定、边界条件确定），理论上通过正装分析、 倒拆分析及倒拆－正装分析相结合的方法，可给出拱肋、主梁理论安装坐标。 但实际施工过程中，一方面主梁、拱肋制作及安装不可避免存在偏差，对于钢主梁、钢拱肋，焊接后局部将会产生一定的变形；另一方面拱肋、主梁架设考虑了活载部分的预拱度已进行预抬高。 这两方面因素将导致吊索上下锚点实际坐标与理论坐标存在偏差，如果按已知的成桥状态计算出的无应力长度进行下料，将导致最终成桥状态结构内力出现较大偏差。

吊索有应力长度修正计算思路：在主梁、拱肋架设阶段，假设吊索上锚点理论坐标为（xi′, yi′, zi′），下锚点坐标为（xj′, yj′, zj′），施工过程中实际上下锚点与理论上下锚点的偏差为（dxi, dyi, dzi）与（dxj, dyj,dzj），实际上下锚点坐标分别为（xi″,yi″,zi″）、（xj″,yj″,zj″）

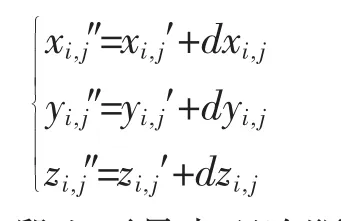
则可计算该阶段上下吊点理论距离D（见公式6）及当前阶段上下吊点的距离D′（D′已包含拱肋、主梁坐标安装误差及预拱度两方面影响因素，见公式7），求出吊索有应力长度修正量ΔL（见公式8），然后求出成桥吊索有应力修正长度L′（见公式9）。 最后结合公式5 求出修正后吊索无应力下料长度，整体计算流程如图1。

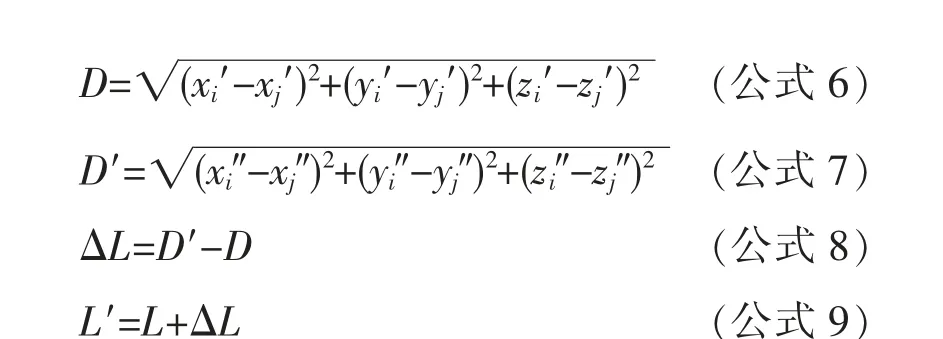
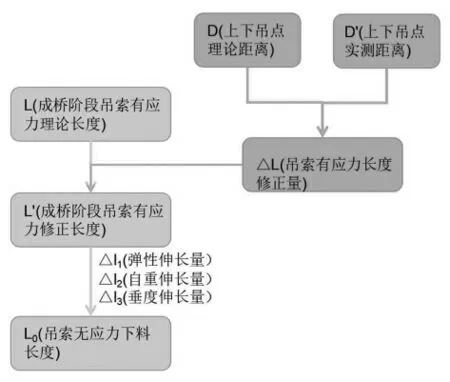
图1 吊索无应力下料长度计算流程图

2 项目概况

某桥为两跨简支提篮系杆拱桥，单跨计算跨径142 m，矢高32 m，矢跨比L/4.44，桥面总宽32 m，桥梁布置图见图2、图3。 拱肋采用全焊钢箱结构，横向设置两片，拱轴线采用二次抛物线，内倾角9°。主梁采用焊接扁平钢箱梁，单箱三室截面。 单跨简支系杆拱设置23 对吊索。 吊索位于拱肋平面内，纵桥向间距为5.8 m。 靠近拱脚处的吊索采用Φ75 mm 等强合金钢拉杆，屈服强度为650 MPa，单跨共4 根。 其余吊索采用Φ5.0 mm-109 低松弛预应力镀锌平行钢丝束，标准强度1670 MPa，吊索外包双层PE 防护套，单跨共42 根。 吊索采用双耳内旋套筒调节型锚具，桥面处锚头为张拉端，拱肋处为固定端。 吊索两端锚固均采用吊索耳板穿销轴的锚固构造，其中上方吊索通过销轴与拱肋底面耳板铰接，仅能沿纵桥向转动，吊索下端通过销轴与主梁顶面耳板铰接，仅能横桥向转动。

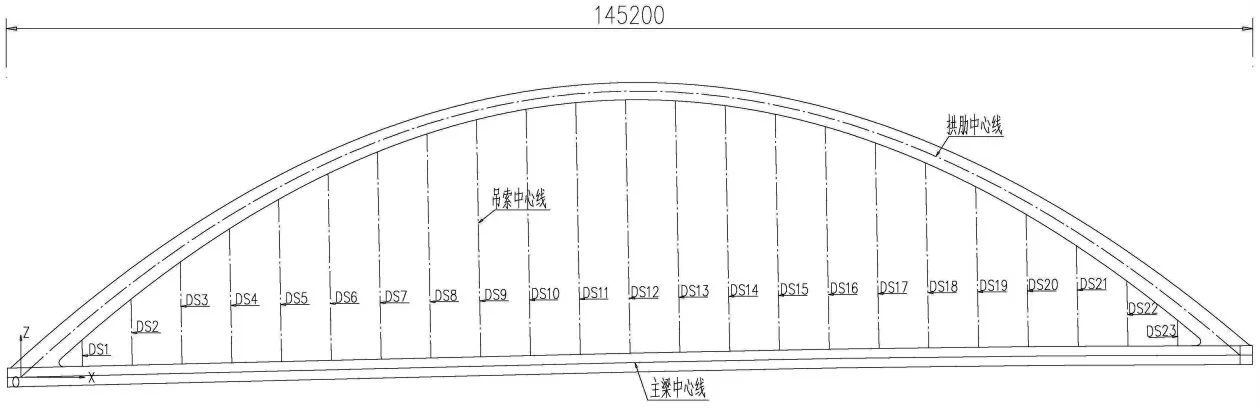
图2 桥梁立面布置图注：图中单位为mm，图3、5、6 同。

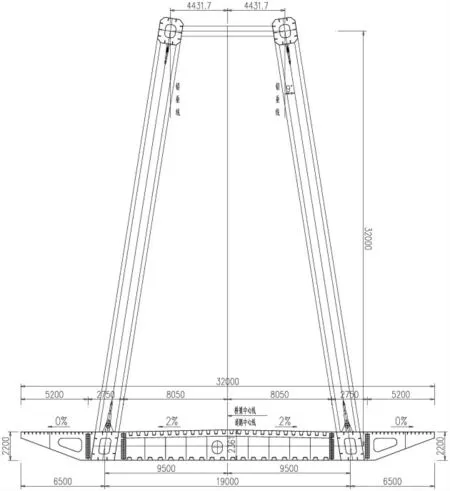
图3 桥梁横断面布置图

3 有限元模型

计算模型采用桥梁结构通用有限元分析软件Midas Civil 进行分析计算。 该桥计算跨径为142 m，主梁、拱肋采用梁单元，吊索采用桁架单元，将桥梁结构离散为空间模型，共207 个节点、163 个梁单元、46 个桁架单元，有限元模型见图4。 主梁、拱肋计算材料参数采用实际试验取值，截面尺寸为关键截面复核值进行修正，通过支架预压试验数据对主梁支架刚度进行修正模拟，拱脚处为主梁与拱肋共用节点进行模拟。

图4 空间有限元模型

4 无应力下料长度计算过程

4.1 吊索有应力修正量计算

主梁、拱肋已架设完成后，吊索上下锚点见图5。当前阶段理论吊索吊点距离通过公式6 进行求解；通过测量拱肋吊耳耳孔外边缘坐标反算出吊耳中心坐标（xi″,yi″,zi″）；通过主梁线形实测坐标，计算出吊索下锚点处计算坐标（xj″,yj″,zj″），通过公式7 求得吊耳上下锚点实测长度D′。吊索成桥阶段有应力修正量ΔL 计算结果见表1。 由表1 可知，最大修正量达到了-57 mm，因此，只有充分考虑建造过程偏差，对有应力索长进行重新修正计算，才能计算出较为精确的吊索无应力下料长度。

表1 吊索上下锚点计算长度及修正量汇总（单位：mm）

图5 拱肋吊索上、下锚点示意图

4.2 成桥阶段吊索有应力修正长度计算

通过成桥阶段主梁、拱肋线形计算吊索有应力长度，通过公式9 求得吊索有应力修正长度，所求结果见表2。

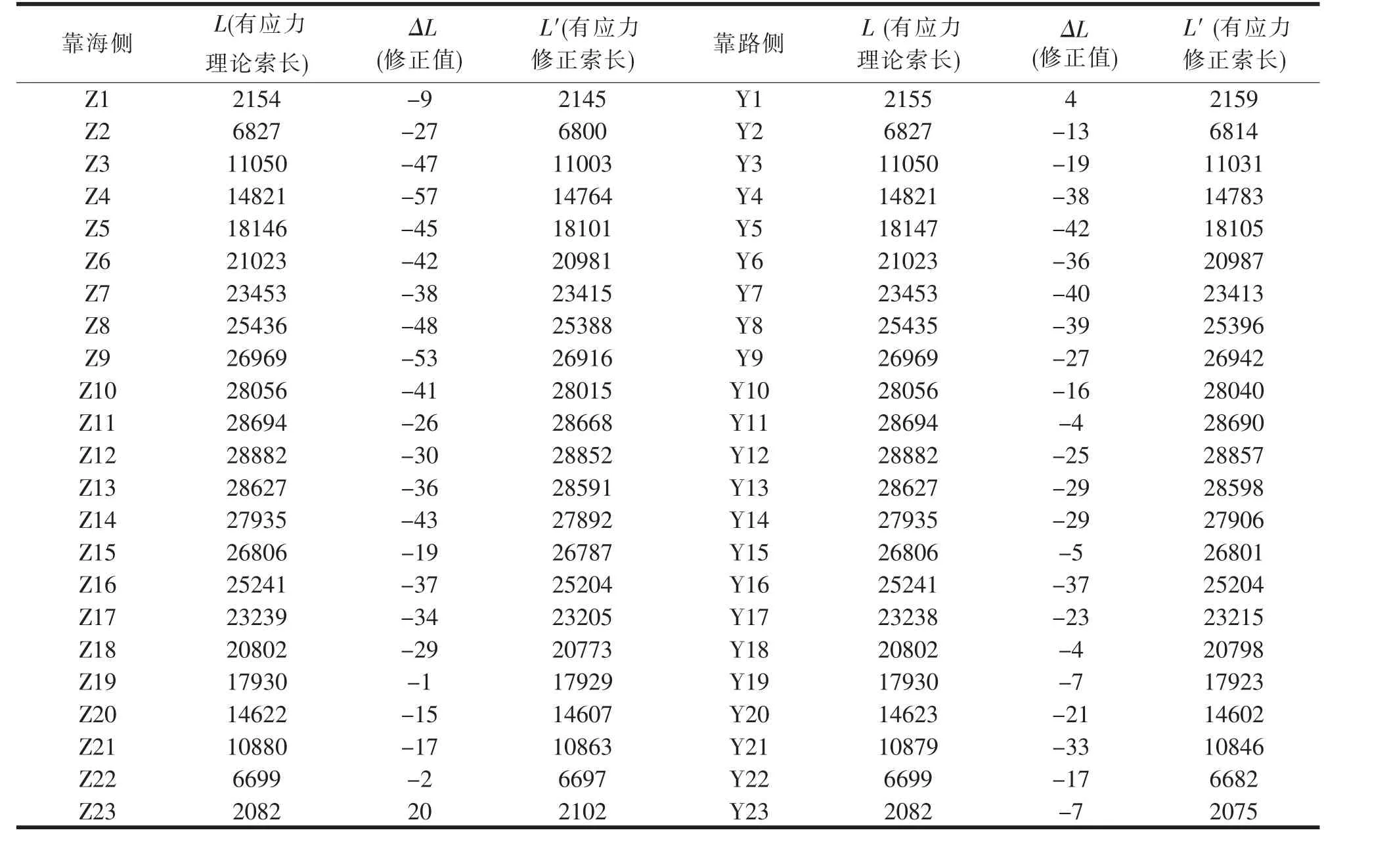
表2 吊索有应力修正长度计算（单位：mm）

4.3 成桥索力计算

对实际主梁、拱肋关键截面尺寸进行复核测量，并对主要材料参数取其试验实测值， 对模型进行修正计算。 由有限元软件Midas Civil 自带的未知荷载系数法及正装迭代法，以主梁的挠度为约束条件，以及以设计成桥状态为目标进行正装迭代分析， 通过两种方法分析对比求得合理的成桥吊索内力（表3）。

表3 左幅1/2 跨成桥索力F（单位：kN）

4.4 吊索自重及垂度伸长量计算

选取跨中最长的一根吊索根据公式3、4 进行计算，计算结果如下：

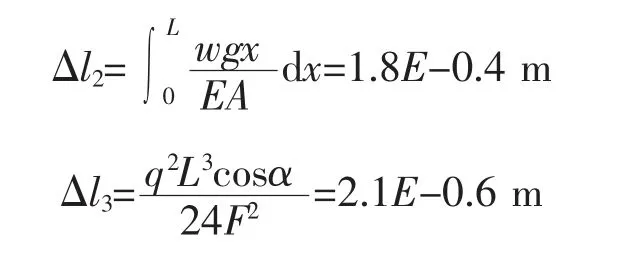
所得结果量级均非常微小，吊索自重及垂度引起的吊索伸长量予以忽略不计。

4.5 吊索无应力下料长度计算

根据已经计算出的吊索有应力修正长度及吊索弹性伸长量， 即可通过公式5 计算吊索无应力下料长度。 46 根吊索无应力下料长度计算结果见表4。 吊索布置图见图6。

图6 吊索布置示意图

表4 吊索无应力下料长度汇总（单位：mm）

5 张拉后吊索实测结果

根据表4 中提供的无应力下料长度，在工厂内预制成品吊索，再运至施工现场进行安装，吊索张拉主要施工步骤包括吊索悬挂、吊索预张拉、吊索张拉及最终调索。 调索完成后，吊索实测索力与理论计算索力见表5， 索力相对偏差在7.9%以内，均符合设计及规范要求。 结果验证了本研究吊索无应力下料长度的修正计算方法是可行的。

表5 部分吊索索力实测值与理论值对比

6 结语

系杆拱桥施工过程中，主梁、拱肋制作及安装存在误差，对于钢主梁、钢拱肋，焊接后局部将会产生一定的变形；拱肋、主梁架设考虑了活载部分的预拱度已进行预抬高。 这两方面因素将导致吊索上下锚点实际坐标与理论坐标存在偏差，如果按已知的成桥状态计算出的无应力索长进行下料，将导致最终成桥状态结构内力出现较大偏差。 无应力索长下料应考虑建造过程偏差的修正。

本文提出的考虑建造过程偏差的无应力索长计算方法，首先在主梁、拱肋架设完成后根据吊索上下吊点实测坐标进行计算吊点距离，与上下吊点理论距离算出吊索有应力长度修正量，然后结合吊索有应力理论长度得到吊索有应力修正长度，最后根据修正后的吊索有应力长度，计算得到了较为精确的吊索无应力下料长度。 经修正得到的吊索无应力下料长度运用于某简支系杆拱桥中，张拉完成后实测数据显示吊索索力符合设计及规范要求。 本研究提出的吊索无应力下料长度计算方法，印证了其实用性，获得良好的效果。