一组非奇异H-矩阵的新实用判据

温立书, 杨 姝, 吕振华

(沈阳航空航天大学 理学院, 辽宁 沈阳 110136)

非奇异H-矩阵(广义对角占优矩阵)在计算数学、矩阵理论、控制论等许多领域有着重要的研究价值和实用价值[1],许多数学问题的解决可以归结为广义严格对角占优矩阵的判定[2]。近年来,一些学者对广义严格对角占优矩阵的判定进行了研究, 得到了许多判别该类矩阵的充分条件[3-10]。本文通过不等式的放缩, 指标集的二次划分给出了判定广义对角占优矩阵的方法,并将结论推广到不可约以及非零元素链情形。

1 预备知识

进一步划分指标集,

定义1 设A=(aij)∈n×n, 若对任意的i∈N有|aii|>Pi(A),则称A为严格对角占优矩阵, 记为A∈D。矩阵A为广义对角占优矩阵当且仅当存在正对角矩阵A使得AX∈D, 记为A∈D*。

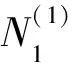
刘建州等[4]给出了如下结论:

定理1 设A=(aij)∈n×n,若

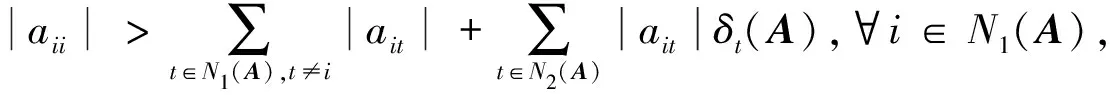
(2)

则A∈D*。

本文通过递进选取正对角矩阵因子元素, 并利用不等式的放缩技巧, 给出H-矩阵的一类新判别方法, 然后将此类方法推广到不可约情形和非零元素链情形。

2 主要结论

下面给出本文的主要结论。

定理2 设A=(aij)∈n×n,若满足

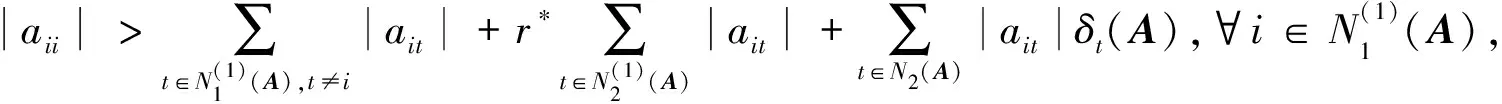
(3)

则A为非奇异H-矩阵,即A∈D*。

证明 根据定义, 只需找出正对角阵X, 使得AX∈D。根据式(1)显然有r*<1, 取很小的正数ε满足

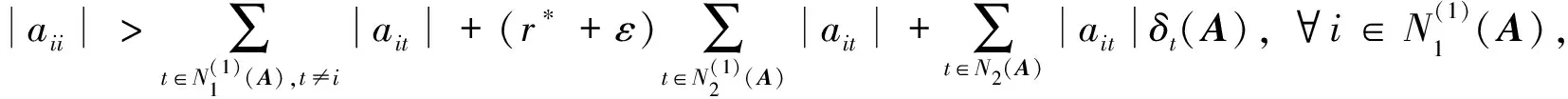
(4)

并且r*+ε<1。取另外一个很小的正数μ, 对于∀i∈N2(A)满足δi(A)+μ<1, 并且使得不等式(5)、(6)成立:

构造正对角矩阵X=diag(x1,x2,…,xn),其中,

令B=AX=(bij), 则bij=xjaij,i,j∈N, 下面证明B∈D。

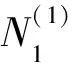
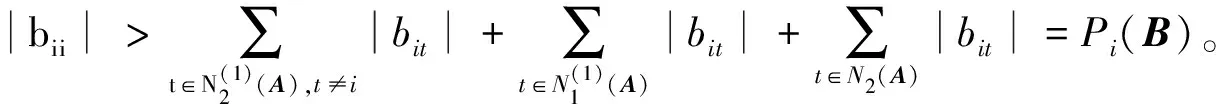
3) 对于任意的i∈N2(A),根据δi(A)定义以及r≥δi(A)可得

综上所述,对于任意的i∈N,有|bii|>Pi(B),因此B∈D,进而可得A∈D*。证毕。

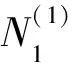
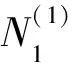
所以矩阵A=(aij)∈n×n满足式(2)的条件时,必满足式(3)的条件。

应用同样的思路考虑不可约矩阵和具非零元素链矩阵的情形,可得以下结论。

定理3 设A=(aij)∈n×n不可约,若满足

并且至少有一个不等式严格成立,则A∈D*。

证明 令X为定理2中构造的n阶对角阵,可得AX为(非严格)对角占优矩阵。根据题意可知,B为不可约矩阵,且至少有一行严格对角占优, 因此B为非奇异H-矩阵。于是存在正的对角矩阵Y, 使得BY为严格对角占优矩阵,从而可得AXY为严格对角占优矩阵。因为XY为正的对角阵, 根据定义,A为广义对角占优矩阵, 即A∈D*。证毕。

定理4 设A=(aij)∈n×n, 若满足以下条件, 则A∈D*。

2) 且对于任意的i∈NJ(A),存在非零元素链air1,ar1r2,…,arkj,使得i≠r1,r1≠r2,…,rk≠j,且j∈J(A),其中

证明 令X为定理2中构造的n阶对角阵,可得AX为(非严格)对角占优矩阵。根据题意可知,B是有非零元素链,因此B为非奇异H-矩阵。于是存在正的对角矩阵Y,使得BY为严格对角占优矩阵。从而可得AXY∈D。因为XY为正的对角阵,根据定义,A为广义对角占优矩阵,即A∈D*。证毕。

3 数值例子

例观察矩阵

经过简单计算可得

从而

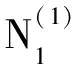
因为

也就是说

应用定理2可以得到A∈D*。

4 结 语

通过二次划分指标集构造新的对角矩阵, 改进了已有的判定非奇异H-矩阵的方法。该方法需要进行大量的计算,但易于用程序实现。近些年不少学者通过判定广义Nekrasov矩阵的方式得到了非奇异H-矩阵的充分条件[7-9], 本文中的技巧和方法同样可以应用到广义Nekrasov矩阵的判定问题上。