基于AdaBoost.RT的污水水质随机配置网络集成模型
赵立杰, 王 月, 郭 烁
(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)
近年来,随着污水排放标准的不断提高,我国对污水处理操作和运行自动化提出了更高要求。活性污泥法是污水处理过程中被广泛采用的方法,其利用活性污泥中的微生物群体,吸附、氧化、分解污水中有机物,经过硝化、反硝化、释磷和吸磷等生化反应去除氮磷污染物,使出水水质满足排放指标要求[1-2]。
污水处理过程是一个典型的非线性、多变量、大滞后、非平稳、时变系统[2],其关键水质参数的检测和控制是污水处理厂稳定、高效运行的重要前提。5日生物需氧量(five-day biochemical oxygen demand,BOD5)和出水氨氮质量浓度等,都是污水处理过程中的重要评价指标。传统的测量方法耗时长、精度不高,在线监测设备价格昂贵、维护困难,因此将软测量技术应用于污水处理过程,建立出水水质关键参数的软测量模型,是解决这一难题的有效途径[3]。
软测量模型建立的方法主要有3种,即基于机理的、基于知识的和基于数据驱动的方法。污水处理过程内部机理复杂,且在这个过程中会产生大量数据,因此当前在污水处理过程中应用较为广泛的是基于数据驱动的建模方法。该方法不需要过程的先验知识,使用过程数据来建立输入输出模型。传统的数据驱动软测量建模方法主要包括多种统计推断技术和机器学习技术,例如将主成分分析(PCA)与回归模型相结合的主成分回归(PCR)、偏最小二乘(PLS)回归、支持向量机(SVM)和人工神经网络(ANN)[4-8]。神经网络具有很强的非线性映射能力,它能逼近任意非线性函数,对复杂系统进行精确建模,因此在污水处理过程建模研究中得到广泛应用[9]。
随机配置网络(stochastic configuration networks, SCN)是Wang等[10]提出的一类随机化学习模型, SCN模型人工干预少、学习速度快。在解决回归问题上取得了良好的性能。 但SCN模型中输出权重由于采样观测原因, 最小二乘解析解可能存在奇异问题。 从而使输出权值不稳定, 出现过拟合。 因此一些改进后的SCN模型被提出, 如L1正则、L2正则、偏最小二乘的随机配置网络[11-13]。 上述改进后的模型既保留了传统SCN的良好逼近性, 又改善了模型过拟合问题, 提高了模型泛化能力和预报精度。
然而,由于神经网络的训练基于经验风险最小化原则,容易产生过拟合和局部优化问题。另外单模型单个神经网络模型的性能是不稳定的,自适应能力差。污水处理过程的工艺复杂,影响重要出水参数测量的因素众多,数据的维数高,这无疑增加了数据驱动建模方法的难度。因此,学者们通过各种技术方法,例如集成方法、正则化方法等,来努力提高泛化能力和稳定性。在上述技术中,集成方法似乎相当有效[14]。
集成学习是通过训练多个学习器,使用一定的策略将学习器结合来完成学习任务。其中最常见的方法有Bagging,Boosting,Stacking等。这些集成方法也被广泛应用于软测量中,并在不同领域发挥作用。文献[15]提出了一种基于改进 Bagging算法的高斯过程集成软测量建模方法。该方法以高斯过程回归算法作为基学习器的学习算法,采用Bagging算法建立高斯过程集成软测量模型。文献[16]提出了基于AdaBoost的BP神经网络算法,并将该方法应用于短期风速预测。还有一些学者采用负相关(negative correlation learning, NCL)算法进行集成,文献[17]以随机配置网络(SCNs)作为基本学习器模型,用负相关学习策略来评估输出权重。在污水处理领域,文献[18]以模糊聚类-极限学习机(extreme learning machine,ELM)为子模型,采用信息熵的元学习机制进行集成。因此和单一模型相比,集成模型具有更好的预测精度。
为了提高水质软测量模型的泛化性,本文采用AdaBoost.RT集成算法对L2-SCN进行集成,以某污水处理厂的过程数据为例,对出水BOD5、NH4-N进行预报。将预测结果与化验值进行对比,结果表明该集成模型具有良好的精度和泛化性。
1 正则化随机配置网络
文献[11]在随机配置网络基础上提出带有L2范数正则化的随机配置网络,改善输出权重最小二乘解析解的代数属性。其中将L2范数作为输出惩罚项,输出权重β由惩罚项和误差项共同决定。

(1)
式中:J为损失函数;N为样本数;β为SCN模型参数;l为某种损失函数(例如,均方误差);r为由标量惩罚系数;α≥0表示加权的正则化项。
加入L2范数正则化后,可以约束β的范围,降低过拟合风险。训练样本{(xn,yn),n=1,2,…,N},其中,xn∈d,yn∈m。X∈N×d和Y∈N×m分别代表输入和输出矩阵,eL-1,q(X)∈N×m代表误差矩阵,其中每一列为
eL-1,q(X)=[eL-1,q(x1),…,eL-1,q(xN)]T∈N。
(2)
式中,q=1,2,…,m。对于输入数据X,第L个隐含节点gL的输出为

(3)
隐含层输出矩阵HL=[h1,h2,…,hL],定义一组变量ξL,q(q=1,2,…,m),

(4)
正值ξL,q越大,输入权值配置效果越好。输出权重矩阵β=[β1,β2,…,βL]T∈l×m确定为
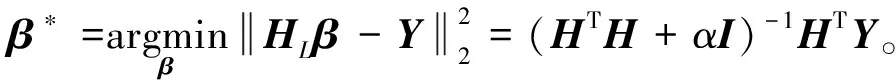
(5)
2 基于AdaBoost.RT的污水水质集成模型
2.1 AdaBoost算法
AdaBoost(adaptive Boosting)是Boosting中最具代表性的算法。Schapire在1990年提出Boosting算法[19],也称提升算法,是集成学习的重要手段,能提高任意学习算法精度。之后Freund和Schapire在将其改进为AdaBoost算法,是一种迭代算法[20]。AdaBoost.RT算法[21]与传统的集成算法Adaboost相比,主要区别在于引进了固定阈值φ,通过与训练误差的对比,确定权值更新的方式。其原理是调整样本的权重分布和弱预报器的权重。在起始状态,每样本的权重相同,开始训练一个弱预报器,根据训练误差来确定其权重,对于预误差相对较大的样本,相应增加其权重。在下一轮迭代训练中,对于误差较大样本给予更多地关注,并相应降低误差较小样本的权重,从而得到新的样本分布。同时,根据弱预报器的预报误差,对弱预报器赋予相应的权重。预报误差越小,权重越大,反之权重越小。经过n次迭代,得到t个弱预报器及其相应的权向量。根据它们的权重,t个弱预报器组合成一个强预报器。
2.2 AdaBoost.RT的正则随机配置网络
基于集成的L2-SCN网络水质预测模型算法的具体计算过程如下。
1) 将数据样本分为训练样本和测试样本,然后初始化训练样本数据权重。初始化权重公式为
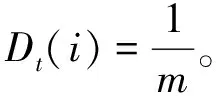
(6)
式中:Dt(i)为初始化权重,i=1,2,…,m;m为训练样本个数,其中误差率εt=0,阈值φ(0<φ<1),迭代次数为T。
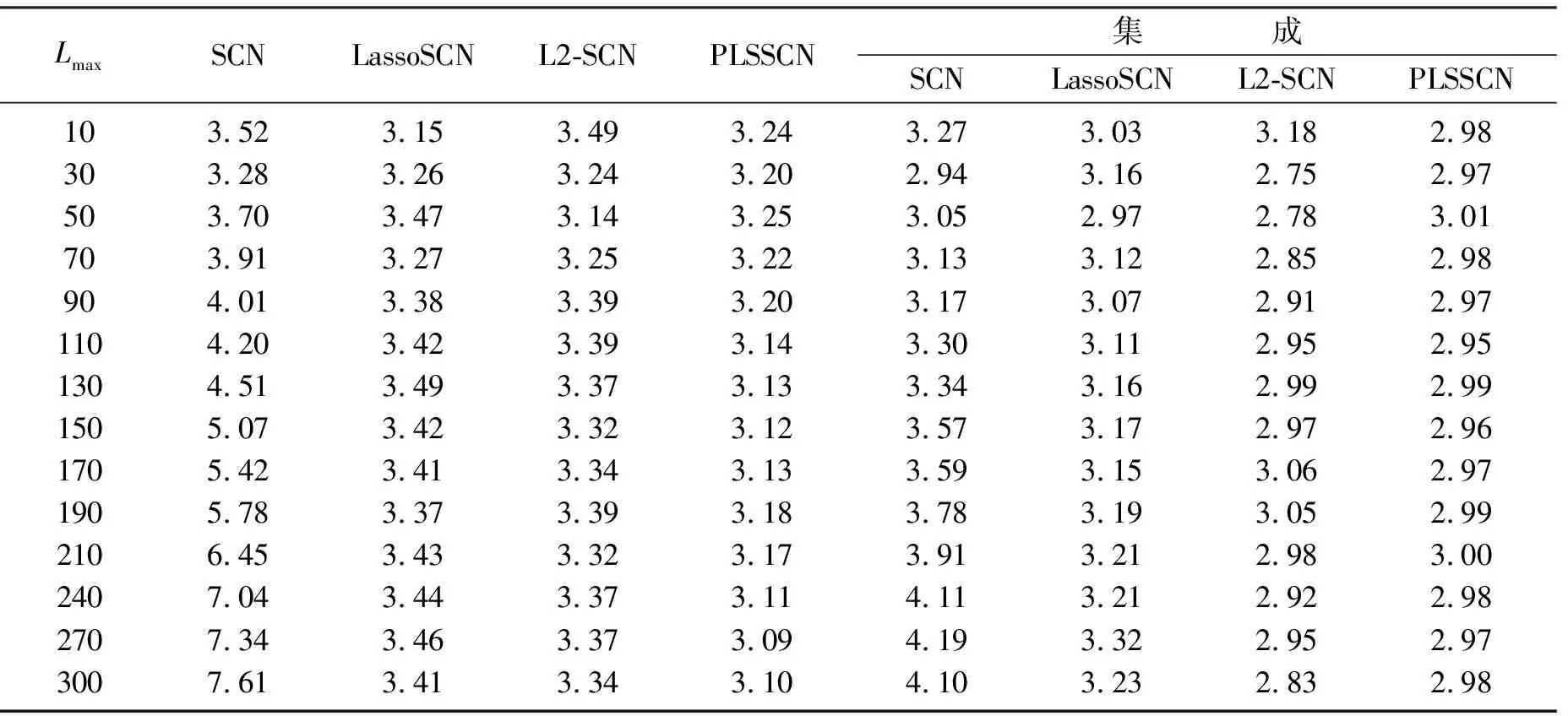
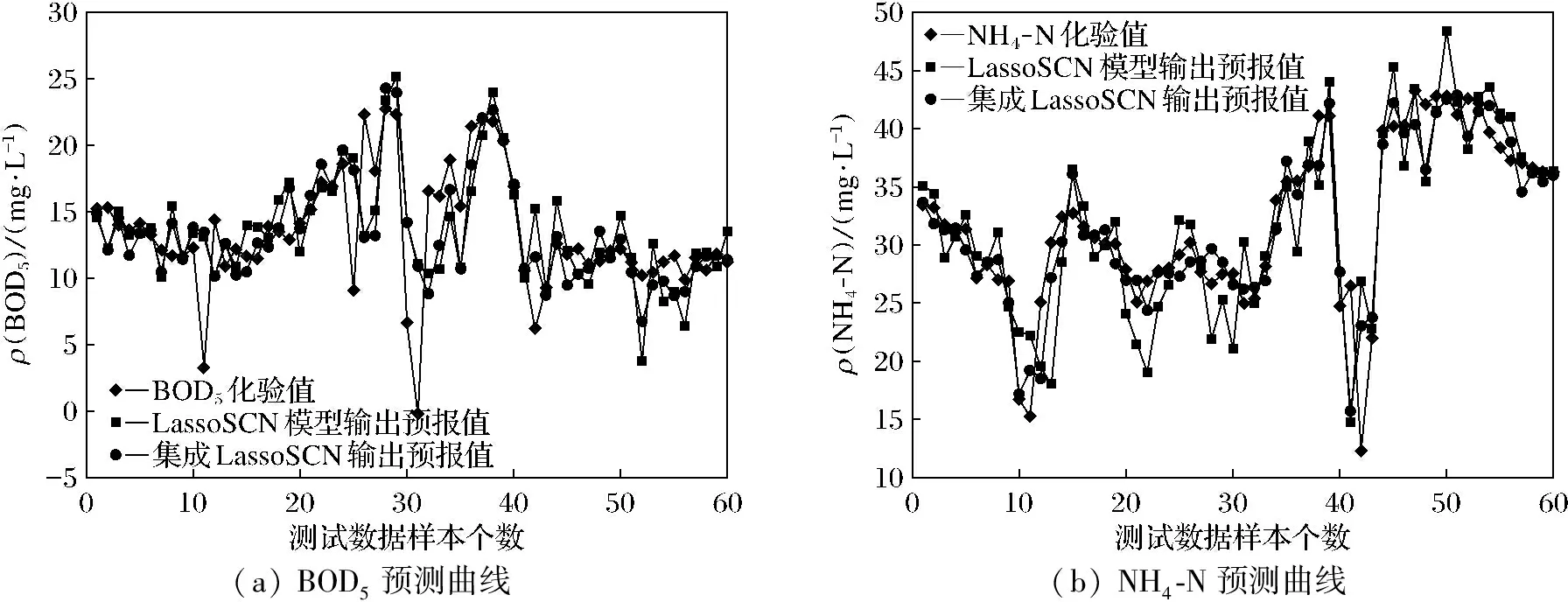
2) 当t (7) 根据相对误差计算误差率 (8) 3) 更新权重。 (9) 式中,Zt是归一化因子。 4) 输出预测结果。由T轮的训练后得到,如式(10)。 (10) 结构简图如图1所示。 图1 集成L2-SCN结构Fig.1 Structure of ensemble L2-SCN 本文所用污水处理过程数据来自沈阳市某污水处理厂, 采样周期以d为单位, 共包含365个样本, 每个样本包含17个输入变量和2个输出变量, 其中输入变量包括进水COD质量浓度、进水SS质量浓度、进水pH值、进水氨氮质量浓度、进水流量、配水计量槽COD质量浓度、配水计量槽悬浮物质量浓度、回流污泥流量、缺氧池氧化还原电位、好氧池氧化还原电位、曝气池曝气流量、缺氧池中溶解氧质量浓度、好氧池中溶解氧质量浓度、生化池污泥体积、生化池pH值、生化池中混合液悬浮固体质量浓度、出水SS质量浓度作为模型的输入变量, 输出变量包括出水BOD5质量浓度、出水氨氮质量浓度。 数据集分为2组, 训练集和测试集, 训练集包括305个样本,X1∈305×17,Y1∈305×2, 测试集包括60个样本,X2∈60×17,Y2∈60×2。 基于上述数据分别建立了SCN、LassoSCN、L2SCN、PLSSCN、AdaBoost.RT-SCN、AdaBoost.RT-LassoSCN、AdaBoost.RT-L2SCN、AdaBoost.RT-PLSSCN污水水质模型。 实验中,设置误差容忍度为0.1,随机配置最大次数Tmax为200,最大隐含节点个数Lmax从10开始每隔20增加到210,之后每隔30增加到300。随机权重范围λ为{0.5,1.0,5.0,10.0,…,250.0},正则化系数为0.2,阈值φ=0.1。实验独立重复运行20次。根据预测的均方根误差(root mean square error, RMSE)评估模型。RMSE的计算公式如下: (11) 表1、表2列出不同隐藏节点设置下,不同建模方法预测的出水BOD5、NH4-N的RMSE统计均值。从表中可以看出,随着隐藏节点的增加,SCN模型测试均方根误差随着隐藏节点的增加而变大,说明SCN在隐藏节点较大时,模型过拟合泛化性差。本文用AdaBoost.RT改进的SCN模型测试均方根误差始终小于SCN模型的均方根误差,相比SCN模型有一定提升,说明集成SCN模型是一个可行的方法,在一定程度上可以防止过拟合现象发生。LassoSCN、L2SCN、PLSSCN模型随着隐藏节点的增加,均方根误差趋于稳定,集成后的模型均方根误差也始终低于单一模型,使模型的预测误差变小,提高了模型的预测性能。 表1 出水BOD5的测试均方根误差对比Table 1 Comparison of test root mean square error of effluent BOD5 表2 出水NH4-N的测试均方根误差对比Table 2 Comparison of test root mean square error of effluent NH4-N SCN,LassoSCN,L2-SCN,PLSSCN模型和集成后的各个模型污水出水BOD5、NH4-N预测值与真实值的拟合曲线如图2~图5所示,可以看出集成后的模型预测能够更好地拟合真实值。与单一模型相比,集成模型预测结果更好,预报更接近真实值。 (a) BOD5预测曲线(b) NH4-N预测曲线 (a) BOD5预测曲线(b) NH4-N预测曲线 (a) BOD5预测曲线(b) NH4-N预测曲线 (a) BOD5预测曲线(b) NH4-N预测曲线 为了更好地验证集成L2-SCN模型的性能,本文与AdaBoost.RT-RVFL、AdaBoost.RT-BP建模方法进行了实验对比,经多次实验对不同隐藏节点进行建模,均方根误差和平均绝对误差作为评价指标,公式如下: (12) 经多次实验,选取每个模型均方根误差和平均绝对误最小值进行对比,如表3所示。从表3中可以看出,在BOD5、NH4-N预测上,集成L2-SCN模型表现更好,均方根误差和绝对误差均最小,预测效果稍好于其他集成SCN模型,通过上述实验对比可以得出,集成L2-SCN模型在出水水质BOD5、NH4-N的预测上有更好的表现。 表3 不同建模方法的测试均方根误差对比Table 3 Comparison of test root mean square error of different modeling methods 由于污水处理关键水质参数BOD5、NH4-N难以准确实时检测,单一模型难以获得良好的预测精度,因此将AdaBoost.RT算法和L2正则随机配置网络相结合进行建模预测,以某污水处理厂真实数据建模仿真,得出以下结论。 1) 与单一SCN模型相比较,将AdaBoost.RT集成算法与SCN相结合,在一定程度上可以克制过拟合的风险,且集成模型预测精度优于任意单一的预测模型。 2) 建立的集成L2-SCN模型,对比同等条件下其他集成模型的预测效果,均方根误差和平均绝对误差都较小,预测模型泛化能力和拟合精度均有一定提高,在污水水质预报上更具有优势。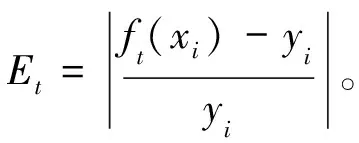
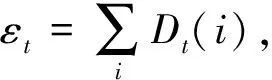
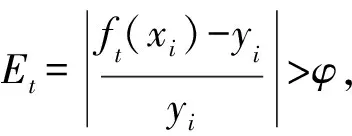



3 仿真实验
3.1 设计与方法

3.2 结果与分析





4 结 论

