基于ICA和LOF的故障检测

郭金玉, 王 霞, 李 元

(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)

在现代工业生产高度智能化的时代背景下,我国致力于先进科学技术的发展与工业生产自动化的提升,现代化的工业过程普遍向智能化、多维度、大规模和高自动化水平方向靠拢。这些特点是提高控制系统稳定性的关键,为工业生产过程的安全性提供保障。近几年,基于数据驱动的多元统计分析方法被国内外许多学者深入研究,并且在工业过程领域取得快速发展[1-4]。在我国,大多数行业通过将设备状态监控与故障诊断手段相结合运用到实际生产过程中。如今故障检测(fault detection,FD)已经成为工业生产过程监控必不可少的手段,故障诊断方法通常可分为4类,即基于数学模型、基于知识、基于数据驱动和基于集合型故障诊断方法。其中数据驱动方法[5]采用统计分析、机器学习和深度学习建立故障诊断模型。这些方法大大提升了自动控制系统的稳定性,确保工业生产过程稳定运行。

非线性已经成为现代实际生产过程的一个普遍且明显的特征,这使得如何有效地提取工业过程中的非线性信息成为故障诊断技术的重要内容。其中多元统计过程控制(multivariate statistical process control, MSPC)是计算机辅助在线过程监控进行故障检测的基本工具之一[6]。MSPC通常通过整合技术来降低数据维数,如主元分析(principal component analysis, PCA)和独立元分析(independent component analysis, ICA)。主元分析将原始数据转换为主元,并使用T2和Q等统计数据来监测该过程。Kresta等[7]证明了主元分析和偏最小二乘法的有效性,并且对核主元分析(kernel principal component analysis, KPCA)无需进行非线性优化做出相关说明。主元分析不可避免地存在局限性,因为主元分析关于数据分布的的假设不适用于实际的工业过程。基于这样的假设,主元分析提取的变量符合高斯分布,而许多实际工业过程中主元分析提取的变量很少符合高斯分布。为了提高非高斯过程的故障检测效果,Kano等[8]将独立元分析应用于故障检测领域。ICA算法主要思想是假设原始样本之间相互独立,不要求数据服从高斯分布,使每个分量最大化独立,便于提取非高斯过程的隐藏信息,以此来提高故障检测的性能。近年来,有研究者提出几种使用独立元分析进行过程监控的方法,如动态独立元分析和核独立元分析。动态独立元分析考虑过程的动态性,而核独立元分析[9]被用来处理非线性过程。关于独立元分析的大多数研究都假设该过程仅由非高斯潜在变量驱动。然而,Ge等[10]提出实际过程总是同时存在高斯和非高斯变量。总之,独立元分析也有局限性,它假设提取的变量服从非高斯分布。主元分析和独立元分析都有一个共同的限制,即假设特定的数据分布很难满足实际工业中的数据分布特征。

本文为了克服现有方法存在的数据分布假设不当而造成的局限性,提出一种新的过程监控方案,该方案将ICA和局部离群因子(local outlier factor,LOF)相结合,以提高工业过程监控的故障诊断性能。所提出的方案具有以下优点:它不必假设监控变量的具体分布,因此它可以处理高斯和非高斯混合分布的潜在变量;由于LOF可以在潜在变量空间中确定非线性决策边界以及无控点,所以与现有方法相比可以更精确地估计控制限,从而可以减少第2类误差。

1 基于ICA和LOF的故障检测

1.1 独立元分析算法(ICA)

提到独立元分析(ICA)算法就会想到著名的“鸡尾酒会”问题,Kim等[11]首先提出ICA的相关概念,并且简单地对ICA进行了一系列的描述,认为ICA是从复杂的线性混合变量中分离出原始的独立潜变量。如果用X和S分别表示混合变量和原始的独立潜变量,它们的关系可以表示为

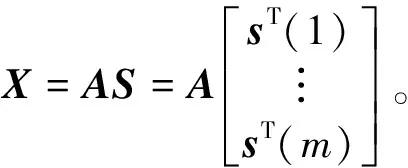
(1)

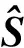
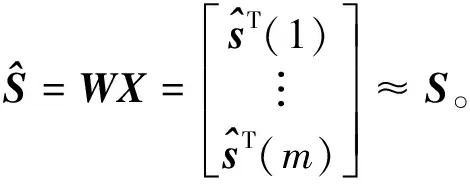
(2)

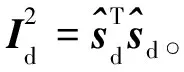
(3)

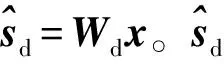
Q=eTe。

(4)

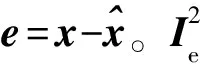
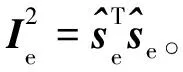
(5)

1.2局部离群因子算法(LOF)

本文采用LOF值(VLOF)作为基于ICA和LOF的监测统计量,以实现更优的效果。由于VLOF的计算与数据的分布或聚类无关,因此它对于高斯和非高斯混合潜在变量的过程监控更为稳健。因为VLOF决定控制限以及观测值中潜变量的非线性边界,所以可以减小第2类误差,这样LOF就比马氏距离更适合与基于ICA的过程监测相结合。

大部分的离群点检测算法都是通过密度、夹角、距离或者划分超平面来决定异常点。这些方法都是从度量数据点相似度的角度出发来判断哪些数据是异常值。LOF 算法是建立在数据点密度基础之上的一种离群点检测算法,准确度高[14]。

Breuning等[15]最早提出局部离群因子的概念,通过给每个数据点分配一个依赖于邻域密度的离群因子来定量分析其离群程度,进而有效地判断样本中数据点是否为离群点。LOF方法的优点在于通过近邻距离的计算,能够消除非线性、多模态特性等对数据的影响,使数据集融合为单模态数据;相对密度的计算能够调整数据的疏密程度使各模态数据的方差近似相等[16]。

LOF算法的具体步骤如下。

1) 计算k-距离。计算第k个最近的物体与物体p的欧几里德距离并定义为k-距离,其中参数k是近邻的数量。

2) 构造p的k-近邻集。集合TkNN(p)由距离p的k-距离内的对象构造。

3) 计算p的可达距离。TkNN(p)中p到对象o的可达性距离计算为

rdk(p,o)=max{kd(o),d(p,o)},

式中,d(p,o)是p到o的欧几里德距离。

4) 计算p的局部可达性密度(local reachability density, LRD)。定义为DLRk(p),

(6)

5) 计算p的LOF值。p的LOF值定义为VLOF(p),

(7)

式中,VLOF(p)是TkNN(p)的平均密度与p的密度之比,当其值小于1时,p不是孤立的离群点,反之,p是一个孤立的离群点。Lazarevic等[17]比较了包括LOF、最近邻法、马哈拉诺比斯法和无监督支持向量机算法(support vector machine, SVM)在内的离群点检测算法的能力,表明LOF算法最好。

1.3 基于ICA和LOF的故障检测

基于ICA和LOF的故障检测包括2个部分:离线建模和在线故障诊断,其检测流程图如图1所示。

1) 离线模型建立。

① 采集训练数据集X,利用均值和方差进行标准化;

② 建立ICA模型,获取独立元;

③ 运用LOF模型剔除离群点;

④ 重新建立数据集,并通过ICA选取新的独立元S;

⑤ 对时刻t的独立元S(t),加入时滞输入特性S(t-1)和时差输入特性S(t)-S(t-1),生成增广矩阵Snormal,

Snormal=[S(t),S(t-1),S(t)-S(t-1)];

(8)

⑥ 运用式(7)计算LOF值;

⑦ 运用核密度估算LOF的控制限。

2) 在线故障检测。

① 测试数据Xnew运用离线建模数据的均值和方差进行标准化;

图1 基于ICA和LOF的故障检测流程图Fig.1 Flow chart of fault detection based on ICA and LOF

② 标准化后的测试数据投影到ICA模型上,获取新的独立元Snew;

③ 对时刻t的独立元Snew(t),加入时滞输入特性S(t-1)和时差输入特性S(t)-S(t-1),将其生成增广矩阵Stest;

④ 将增广矩阵Stest投影到LOF模型上,计算LOF值;

⑤ 通过LOF值与控制限的对比,检测数据是否正常。

2 仿真结果与分析

田纳西-伊斯曼过程(Tennessee-Esatman, TE)是由Downs等[18]于1993年设计的模拟实际工业过程的仿真平台,该数据集已广泛用于优化、预测控制、过程诊断和控制教育等研究,并取得许多先进科研成果[19-20]。

TE过程工艺复杂,具有数量庞大的变量。图2是TE过程的工艺流程图。

图2 TE过程的工艺流程图Fig.2 Flow chart of TE process

在实验仿真中,使用TE过程生成的数据,采用了Lee等[21]提出的过程设计,其中观测变量由41个过程测量值和11个操作变量组成。首先对实验数据进行标准化,以避免由于变量之间的标度差异而导致的不准确性问题。使用500个正常样本组成训练集建立监控模型,监控21种故障。对于实时监控阶段,每种故障类型包含960个观测值,故障在样本161处引入。

采用TE过程的21个故障进行仿真测试来验证算法的有效性。将500个正常样本进行独立主元分析,获取独立主元S,然后进行时滞和时差操作并将数据进行组合,得到训练数据集的增广矩阵用于建立LOF模型,对测试数据进行检测。以故障16和故障19为例,对比传统的ICA、LOF和本文方法的检测性能。故障16和19的检测结果分别如图3和图4所示。

(a) ICA-I2d(b) ICA-I2e(c) ICA-Q(d) LOF(e) 本文方法

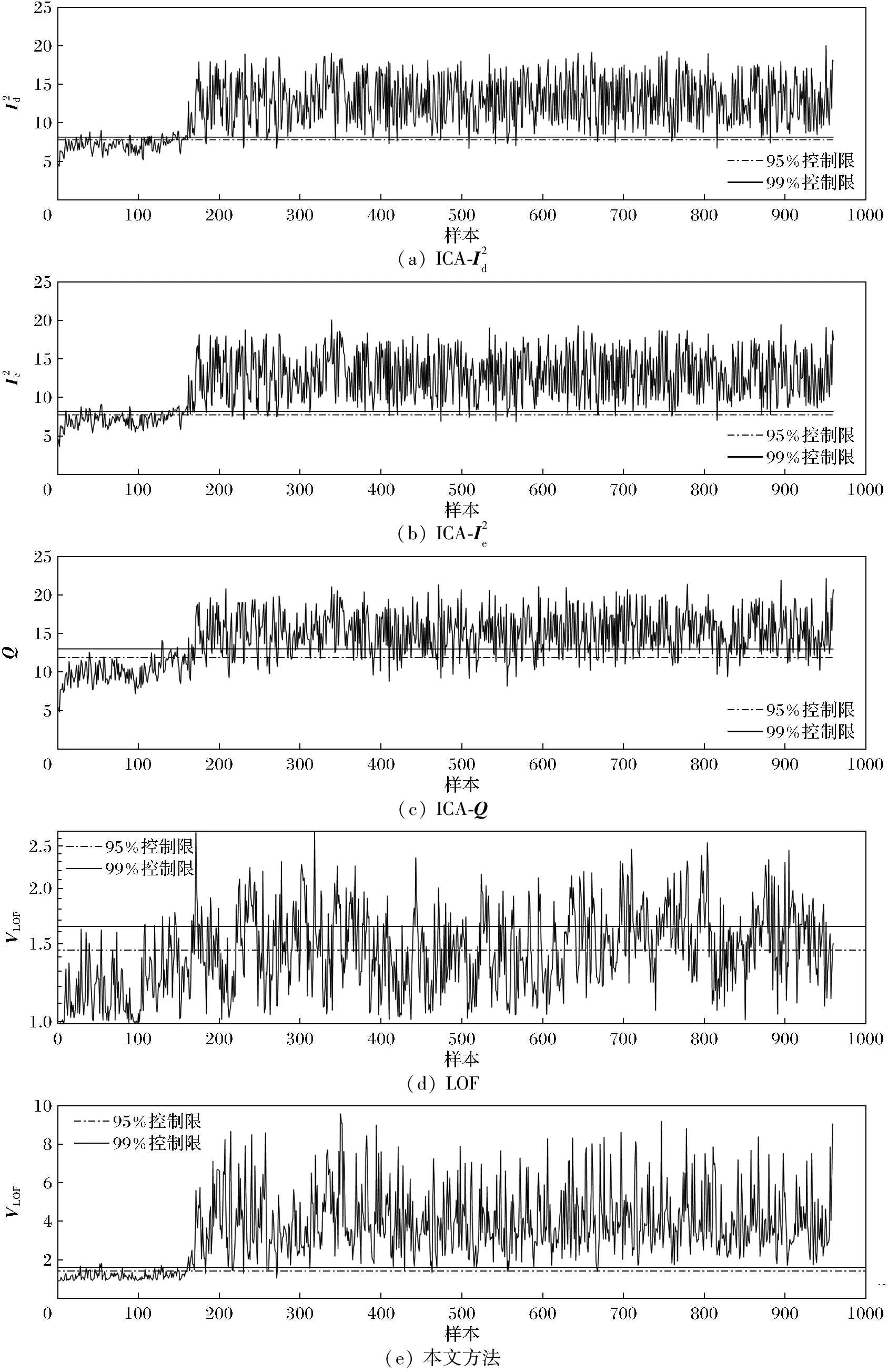
(a) ICA-I2d(b) ICA-I2e(c) ICA-Q(d) LOF(e) 本文方法

从图3可以看出,LOF算法可以检测出故障但是存在明显的误报,并且在引入故障数据后很多时刻的统计量均低于控制限,漏报情况十分明显,这是因为LOF算法是一种基于密度的检测算法,要求检测的数据具有明显的密度差异,而TE数据的密度差异较小,所以该算法对数据的异常检测效果比较差。ICA的3个统计量都可以检测出绝大部分的故障,但是也存在误报。这是因为TE过程的数据是高斯与非高斯混合的分布,ICA能够有效提取数据中的非高斯特征,无法提取数据的高斯特征,影响其检测效果。本文算法的故障检测效果优于传统的ICA和LOF,这是因为在建立模型之前剔除了数据中离群程度较高的数据,运用独立元空间的增广矩阵降低样本的自相关性,提高LOF模型的故障检测效果。故障19的检测效果(图4)与故障16的检测效果(图3)类似,这3种算法都可以检测出故障,但是每种算法都存在不同程度的误报和漏报情况。ICA算法对故障19 的检测效果略差于故障16,Q统计量的漏报情况十分明显。Q统计量反映了在某一时刻测量值对模型的偏离程度,这表明在故障引入后,故障测量值明显偏离了建立的模型,所以产生较为明显的漏报情况。LOF算法对故障19的误报少于故障16,但是漏报情况十分明显。对比3种算法的仿真结果图,本文算法的故障检测效果明显优于传统的ICA算法和LOF算法,并且误报情况极不明显,漏报情况相比于ICA和LOF算法较少,验证了ICA-LOF算法的有效性。

本文运用故障检测率来衡量算法的优越性,表1是各种方法故障检测率的对比。从表1中可以清楚看到,运用95%的控制限时,故障5、10、11、15、16、17、19、20和21的检测率相较于其他方法,都有不同程度的提高。这是因为本文方法在建模之前运用离群因子算法剔除明显孤立的异常点,然后通过独立元分析算法提取混合变量中的非高斯独立元构建增广矩阵,降低样本间的自相关性,提高了LOF算法的故障检测性能,更适合由高斯和非高斯混合分布的工业过程监控。运用95%的控制限时,本文方法的平均故障检测率为83.54%,而运用99%的控制限时,本文方法的平均故障检测率为81.83%,高于其他2种方法,验证了该方法的有效性。

表1 各种算法对TE过程故障检测率对比Table 1 Comparison of fault detection rate of various algorithms on TE process 单位:%

3 结 论

本文提出一种基于ICA和LOF的故障检测方法。通过ICA提取独立主元,引入其时滞输入特性和时差输入特性,将3者组合成增广矩阵作为LOF的输入,运用LOF进行故障检测。将此方法应用到实际的TE过程中,仿真结果表明,与ICA、LOF方法比较,本文方法有效提高了故障检测率,降低了误报率,验证了方法的有效性。这说明独立主元分析预处理方案能够有效地提取混合变量中的非高斯信息,同时基于独立元空间增广矩阵的LOF方法更适合于由高斯和非高斯混合分布的工业过程监控。

本文主要研究基于ICA和LOF的算法在工业过程故障检测中的应用,但是该算法对微小故障的检测效果较差,因此,下一步将继续努力改进该算法并将其运用到微小故障检测领域。