拟线性Kirchhoff-Schrödinger-Poisson系统解的存在性
康红霞, 黄永艳
(山西大学 数学科学学院, 山西 太原 030006)
考虑以下的拟线性Kirchhoff-Schrödinger-Poisson系统

(1)
非负解的存在性。 其中:Ω是3中的一个具有光滑边界的有界区域;a>0,b≥0是常数;ε>0,λ>0是参数;u、φ是x的函数。
首先,假设非线性项f∈C1()满足以下条件:
(f1)f(t)=0,t<0;
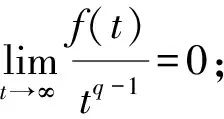
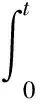
Kirchhoff-Schrödinger-Poisson系统是非线性Schrödinger方程、irchhoff方程和Schrödinger-Poisson系统的结合。式(2)为Schrödinger-Possion系统。
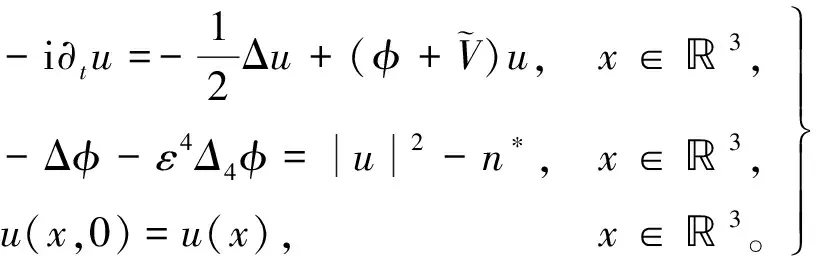
(2)
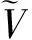
文献[1]研究了系统(3)基态解的存在性,并且研究了当ε→0时解的行为,以及这些解收敛于ε=0时,对应于式(3)的Schrödinger-Poisson系统的基态解。
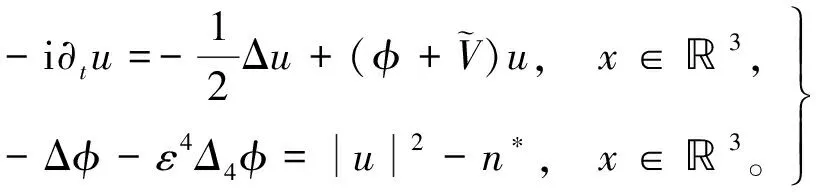
(3)
文献[3]研究了系统
基态解的存在性和渐进行为,其中K∈L2(3),a是一个正的有界连续函数。
文献[4]研究了有界区域上具有临界非线性项的二元系统,并获得了系统的解。
受文献[1-4]的启发,本文研究拟线性Kirchhoff-Schrödinger-Poisson系统(1)非负解的存在性。
下面给出本文的主要结果。
定理1 假设(f1)~(f3)成立,则存在λ1>0,使得对任给的λ>λ1和ε>0,系统(1)存在非负解。
在假设条件成立的前提下,上述定理说明了当λ充分大时,系统(1)存在非负解。
因为参数ε>0和λ无关,所以为了简便起见,以下设ε=1。
1 准备工作
对r∈[1,∞),用Lr(Ω)表示通常的Lebesgue空间,其范数为

回顾文献[5]中的Simon不等式。设p≥2, 则存在Cp>0, 使得对所有的x,y∈3,都有
|x|p -2x-|y|p -2y,x-y≥Cp|x-y|p。
(4)
用C,C1,C2,…表示正常数,它们可能在行与行之间不同。
现在定义系统(1)相应的能量泛函,
2 主要结果的证明
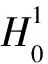
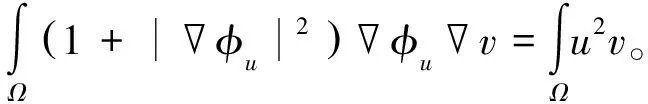
(5)
证明 定义算子A:X→X*,
首先证明A是连续的。假设{φn}在X中收敛到φ,则对任给的v∈X,
因此,A是连续的。
再证明A是强单调算子。事实上,设φ1,φ2∈X,运用不等式(4),有
所以A是强单调的。
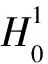
易证Gu是X上的有界线性泛函,运用Minty-Brouder定理完成证明。
从引理1还可以得出
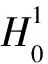
定义泛函
则有
文献[2]中证明了非线性部分W是C1的,且其Fréchet导数为

下面定义Jλ的截断泛函。考虑光滑截断函数ψ:[0,∞)→[0,1], 满足
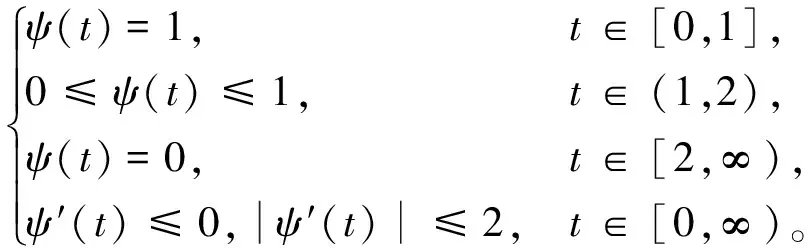
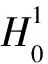
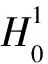
证明 首先证明tλ的存在性。根据条件(f1)和(f2),对充分小的η>0,存在正常数C(η), 使得
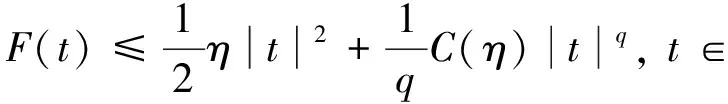
(7)
选取t>0充分小,运用Sobolev嵌入定理,
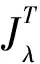
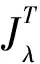
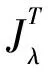
即
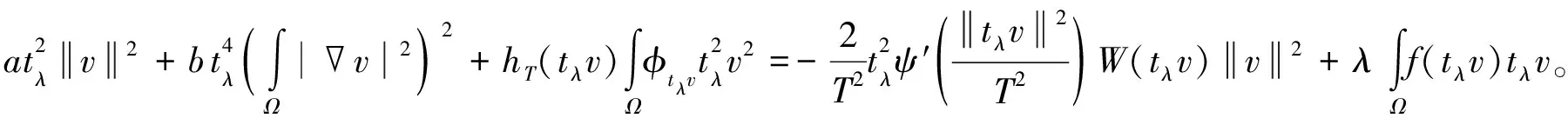
(8)
运用(f3),可以得到
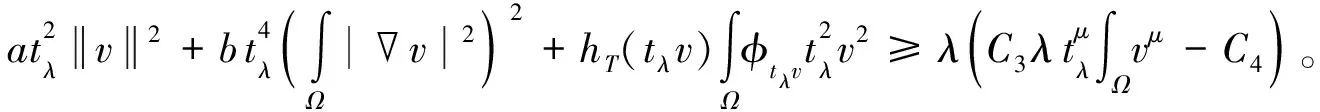
(9)

这是不可能的,所以{tλ}在[1,∞)上有界。
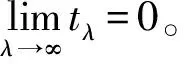
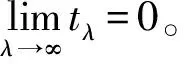
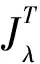
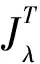
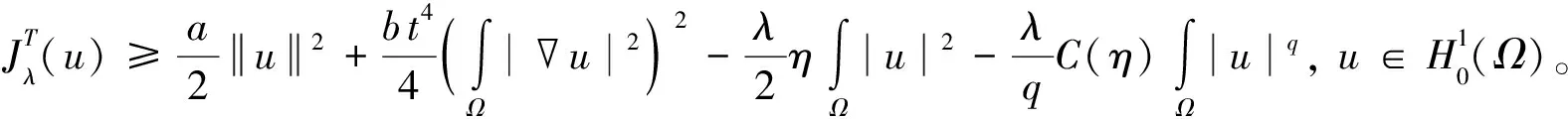
(10)
取η充分小, 运用Sobolev嵌入定理,可得
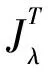
(11)
因为q∈(4,6),所以可取ρ>0充分小,使得结论成立。
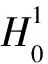
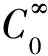
注意到μ∈(4,6), 可以取t>2T充分大且eT∶=tv, 使得结论成立。
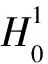
这里

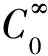
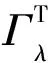

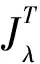
证明 先证明{un}是有界的。事实上,
所以{un}是有界的。
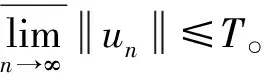
根据条件(f1)、(f2),Hölder不等式以及{un}的有界性,可得
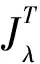
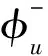
特别当ε=0时,相应的Kirchhoff-Schrödinger-Poisson系统如下,

(12)
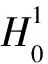
3 结 论
本文利用山路定理和截断技术等方法研究了拟线性Kirchhoff-Schrödinger-Poisson系统解的存在性问题,得到了其存在非负解。

