GFRP管钢骨高强混凝土轴心受压柱力学性能有限元分析

李 檀, 周 乐

(沈阳大学 建筑工程学院, 辽宁 沈阳 110044)

GFRP管钢骨高强混凝土柱是由3种不同材料组合而成,即由GFRP管-高强混凝土-工字形型钢组合形成的轴压受力试件。该组合试件在钢骨高强混凝土试件的基础上增加了按照特定角度缠绕的GFRP管,通过GFRP管对混凝土的约束作用进一步提升了原试件结构的承载力。GFRP作为一种新型材料,因其强度高、质量轻、可塑性强的特点作为传统建材的一个重要补充,被赋予了较高期望[1]。但目前我国对于这种新型组合试件的理论研究还需完善,因此用有限元模拟对试件进行力学性能模拟是必要的。

ABAQUS有限元分析作为建筑物安全性评估的重要手段,可根据拟建工程与相邻建筑物信息、相互关系、围岩条件及附加载荷,结合定性分析进行有限元数值模拟计算,并可根据结构的应力、变形和内力变化情况,定量分析拟建工程对相邻建筑物的安全性影响[2]。本文结合相关文献的研究成果,通过ABAQUS有限元分析软件还原建立了GFRP管钢骨高强混凝土的轴向承载力有限元模型,并与已有试验结果进行对比,证明模拟分析的正确性。

1 有限元模型的建立

本文模拟的试件外径为200 mm,柱高为600 mm,混凝土强度等级为C70,钢骨采用I10号工字钢,各试验柱主要参数见表1,模型如图1所示。其中工字钢和混凝土建立为实体拉伸模型并嵌套装配,组合前对混凝土模型进行切削拉伸处理。GFRP管建立为壳体拉伸模型并与实体模型嵌套装配,采用壳体类型的好处是方便对比修改模型中GFRP试件的厚度。

1.1 材料本构关系

在有限元软件模拟步骤中,建立材料本构关系模型是整个环节的核心步骤,需要建立准确且适合所要模拟分析的对象,充分了解分析材料的性能、试件本身的特性、有限元方法基础以及软件本身的计算方法等[3]。本文数值模拟计算中所使用的混凝土本构关系模型采用了文献[4]试验测得的C70混凝土材料性能试验数据与Kent-Park三阶段混凝土塑性损伤模型(压缩损伤)[5],这是一种足够成熟的用来分析混凝土结构在动载荷下的分析模型,能够满足本次模拟的需要,模型数据曲线如图2所示。工字钢弹塑性为各向同性,选用了与原有材性试验接近的Q355高强钢国家标准值来减少试验误差。GFRP壳体的本构关系尚难有足够成熟完善的模型,本文参照了文献[6-9]提出的FRP约束混凝土圆柱体的强度计算简化模型,模拟结果和已有试验结果吻合良好,GFRP材料性能如表2所示。

1.2 接触模型的建立

本文讨论的接触关系主要是GFRP纤维、混凝土及工字钢之间的接触关系,其黏结滑移对模拟结果影响不大,故本文在组合框架的有限元建模过程中不考虑GFRP纤维、钢骨与混凝土之间的黏结滑移[10]。采用平截面基本假定,在允许的范围内采用了比较简化的接触关系。GFRP管壳体与混凝土之间的接触关系有切向与法向,切向选用了摩擦系数为0.2的各向同性的摩擦接触,法向选用了允许接触后分离的硬接触,其余选项皆为软件默认值,钢骨与混凝土之间的接触关系采用嵌入处理。

1.3 单元选取

模拟中混凝土和工字钢均采用8节点减缩积分格式的线性六面体单元,即C3D8R实体单元,其中“C”代表应力-位移实体单元,“3D”代表实体单元是三维维数,“8”代表单元的节点数目,“R”代表减缩积分,当单元具有规则形状时,所使用的Gauss积分点的数目足以对单元刚度矩阵中的多项式进行精确积分[11]。外层GFRP管采用4节点减缩积分格式的符合材料壳单元,即S4R壳单元,这种单元的特点是允许横向剪切变形,是通用壳单元的一种。

1.4 网格划分

在有限元模型的建立中,网格的划分尤为重要,本文模拟的网格划分考虑到混凝土内置工字钢的影响,选用了自由网格划分,自由网格划分具有更大的灵活性,且对划分时结构单元的几何形状要求不高[12],具体划分如图3所示。

2 有限元模型验证

图4为试件GSC1的有限元模拟与试验结果,从图中可以看出,无论在弹性阶段还是弹塑性阶段,二者的承载力变化曲线吻合良好。

图5～图8为试件应力云图,从图中可以看出,各材料之间保持着较好的协同关系,试件的最终破坏模式为端部局部屈曲破坏[4],且破坏时试件均未坍塌,证明了有限元模型的正确性。

3 参数分析

通过图5～图7的对比可以看出,在3个试件中钢骨的破坏形态最为相近,钢骨的形变直观地反映了载荷的增加。而混凝土破坏形态的差异反映了参数改变对模拟模型破坏结果的影响, GFRP管对于混凝土形变有一定约束作用。

3.1 GFRP管壁厚度

从模拟试验结果来看,壁厚为5 mm的试件GSC2极限承载力大于壁厚为3 mm的试件GSC3的极限承载力,即随着GFRP管壁厚度增加,试件的极限承载力和轴向极限应变都有所提高,即代表GFRP管提供的侧向约束更强[13]。为了进一步验证这一假设,将管壁厚度为7 mm、其余参数与GSC2、GSC3相同的试件GSC4的数据输入模型中,得到的承载力与试件GSC2、GSC3承载力变化曲线如图9所示。在试件加载的弹性阶段模拟数据与试验数据吻合良好,但在屈服阶段,试件GSC4的极限承载力明显大于GSC1和GSC2的极限承载力,且3组数据之间极限承载力提升幅度符合线性分布,证明了管壁厚度对试件核心承载力提高具有积极的影响。

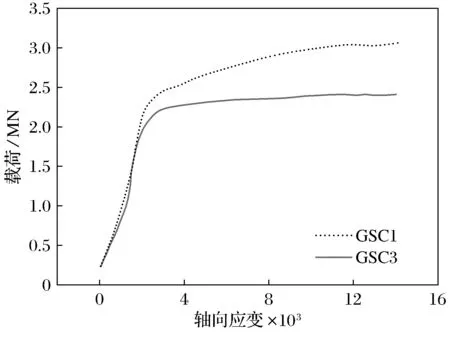
图10 试件GSC1与GSC3承载力变化曲线

3.2 GFRP管纤维缠绕角度

模拟不同纤维缠绕角度主要依靠改变GFRP壳体Hashin损伤模型中不同方向的纤维强度来实现,在此操作下得到的试件GSC1和GSC3承载力变化曲线如图10所示。从图中可以看出,初始阶段缠绕角度较小的试件GSC1与试件GSC3相差不大,但试件GSC1的极限承载力却高于试件GSC3。这是因为在施加载荷的初期,GFRP管的约束作用表现并不明显,直到进入弹塑性阶段,GFRP管的约束能力才开始发挥作用。由此可知,缠绕角度较小,即越接近环向缠绕的试件环向紧箍力越强,对混凝土有着更好的约束能力。

3.3 模型破坏形态

通过对图4、图5模型破坏形态与承载力变化曲线的分析可知,GFRP管的破坏出现在载荷达到极限载荷的60%左右,而直至载荷达到极限载荷的80%左右,模型的承载力才进入屈服阶段,这说明在此期间GFRP管通过约束作用对混凝土施加了环向的紧箍力,从而使混凝土处于三向受力状态,提高了模型的承载力。

4 结 论

1) 有限元模拟结果与文献试验结果吻合良好,证明了GFRP管钢骨高强混凝土轴压模型的正确性。

2) GFRP管钢骨高强混凝土轴心受压试件的承载力随着GFRP管壁厚度的增大而增大,随缠绕角度的增大而减小。

3) 通过对模型破坏形态和数据曲线的分析可知,GFRP管通过约束作用使混凝土处于三向受力状态,抑制了混凝土的形变,达到提高承载力的效果。