激光测振仪中最小均方误差前向预测器的研究
王之昊,张文喜*,伍 洲,孔新新,王永彪,郝义伟
1中国科学院空天信息创新研究院,北京 100094;2中国科学院大学光电学院,北京 100049;3中国科学院计算光学成像技术重点实验室,北京 100094
1 引言
激光测振仪具有测量精度高、测量距离远、测量频带宽和非接触式测量等优点,广泛应用于环境振动测量、技术侦察、无损探伤、机械监测等领域[1-5]。激光测振仪通过解调振动引起的多普勒频移获取目标的振动信息。由于测量过程中存在系统和外界环境的振动、电路系统热噪声、环境光干扰、散粒噪声等因素引起的噪声[6-7],主要噪声形式为高斯噪声和1/f 噪声。这些噪声导致激光测振仪的振动测量精度受到振动测量信号信噪比的影响,所以对振动测量信号进行滤波是提高激光测振仪精度的关键[8]。
近年来,国内外针对振动测量信号的滤波开展了大量研究。Saho 等[9]在测振仪中采用了alpha-beta 滤波技术,能够较好地跟踪信号的相位,缺点是直接叠加了原始信号加权,导致滤波信噪比较低。Shao 等[10]提出了鲁棒自适应卡尔曼滤波,提高了系统的鲁棒性并且滤波信噪比较高,缺点是算法结构复杂,硬件难以实现。张达等[11]采用的小波消噪计算量小,时效性好,但是存在非线性的问题,会导致滤波后的相位失真,影响相位解调精度。吴俊[12]等采用基于多尺度一维卷积神经网络的振动识别算法,可以有效识别光纤振动传感信号。张永康[13]等采用了分布式光纤入侵信号识别技术来消除光纤振动信号的背景噪声,很好地对入侵事件进行识别。刘帆等[14]在激光测振仪中采用了最小均方误差(LMS)自适应滤波算法,能够有效提高测量振动信号的信噪比,并且有良好的相位保持性。
相较于维纳滤波、卡尔曼滤波等滤波器,自适应滤波器不需要预先知道噪声的统计特性,而是通过逐次迭代将滤波器的工作状态自适应地调整到最优[15],并跟踪输入信号的时变特征。LMS 算法结构简单,相比RLS、NLMS 等自适应滤波算法,其计算复杂度更低,LMS 算法更容易用硬件实现并集成在激光测振仪内部。LMS 算法在应用过程中一般采用陷波器或者前向预测器两种结构,陷波器结构需要获取振动测量信号的噪声分量作为输入,获取难度较大;而前向预测器结构仅需要测量信号作为输入,可以降低算法应用的难度,适用于激光测振仪的LMS 自适应滤波。
为了解决高精度激光测振仪中自适应滤波的难题,本文采用LMS 前向预测器作为激光测振仪的自适应滤波方法,通过理论推导、仿真和实验验证,研究了影响LMS 前向预测器滤波信噪比的因素。仿真和实验验证表明,LMS 前向预测器的信噪比和收敛速度与振动测量信号峰值、滤波器阶数和步长系数有关,并解释了各参数之间作用的机理。为实现激光测振仪自适应滤波的LMS 前向预测器参数设计提供了理论依据。
2 理论推导
2.1 输入信号模型
激光测振仪射出的激光照射到振动物体,反射光叠加了包含物体振动信息的多普勒频移,与参考光叠加发生干涉,并被光电探测器接收。为了从接收到的干涉信号中获得物体振动信息,采用正交解调方法进行解调,流程图如图1 所示。

图1 正交解调流程图Fig.1 Orthogonal demodulation flow chart
光电探测信号S(n)的表达式为
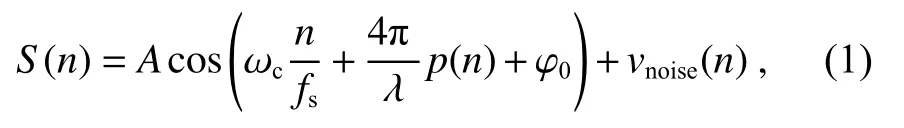
其中:p(n)是物体的位移,ωc是中心频率,fs是采样频率,A是 探测信号峰值。vnoise(n)的主要成分为散粒噪声和热噪声。S(n)经过以 ωc为中心的带通滤波器,其中的噪声变为窄带噪声,可以表示为

其中:ξc(n)和ξs(n)为互不相关的窄带平稳高斯过程,方差σ2与vnoise(n)相同,均值为0,并且中心频率为0 Hz。Sin(n)可以合并为
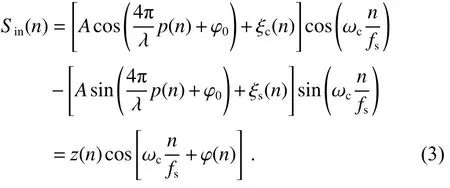
上式中z(n)是信号Sin(n)的包络函数,φ(n)是相位随机变量,表达式为

由式(3)和式(4)知:

所以,z(n)与φ(n)的联合密度函数为
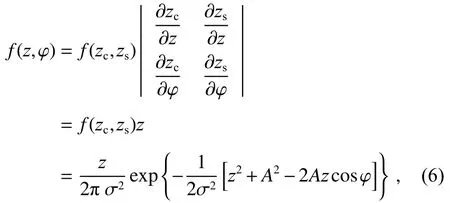
φ(n)的概率密度为
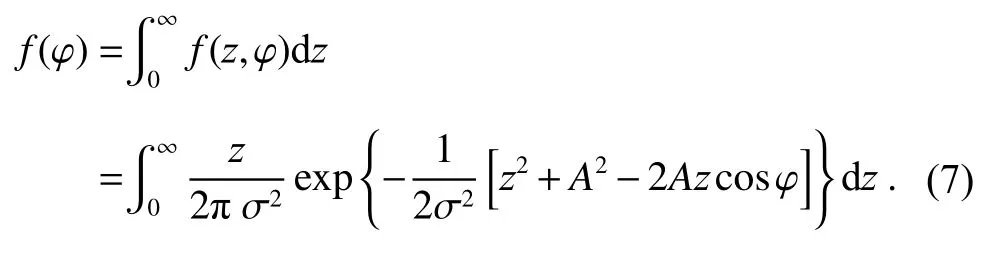
根据文献[16]的相关推导,式(7)的分布近似于高斯分布,即相位随机变量φ(n)的噪声近似于高斯噪声。Sin(n)经过图1 的正交解调系统,得到的正交分量VQ=z(n)sinφ(n)与同向分量VI=z(n)cosφ(n)相除后反正切得到还原的相位信号:

其中:v1(n)为相位信号的近似高斯噪声。由 式(8)可得到物体振动的位移p(n),对于做简谐振动的物体而言,p(n)通常为一单频正弦信号,设为p(n)=对位移进行差分可以获得物体振动的速度。对相位信号求差分并除以系数,得到振动速度测量信号x(n),表示为

2.2LMS 前向预测器
LMS 前向预测器是一种基于最小均方误差准则的自适应滤波器,结构如图2 所示。
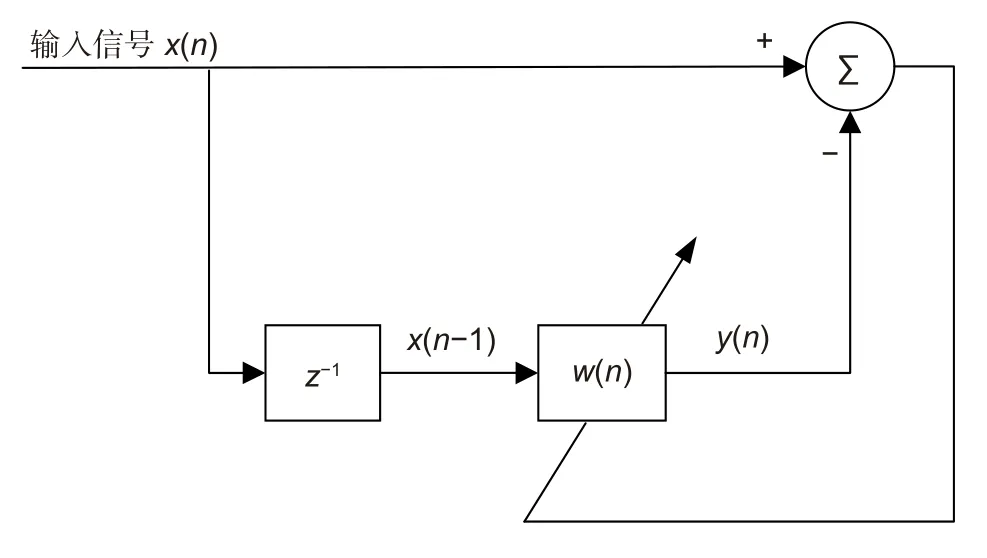
图2 LMS 前向预测器框图Fig.2 Block diagram of LMS forward predictor
前向预测器基于抽头延迟线结构,用第n−1~n−M个数据x(n−1)预测第n个数据x(n)。预测值为
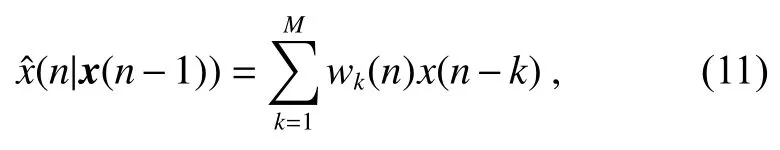
其中:wk(n)表示n时刻滤波器抽头权向量w(n)的第k个抽头权系数。定义前向预测误差e(n)等于输入信号与它预测值的差值:
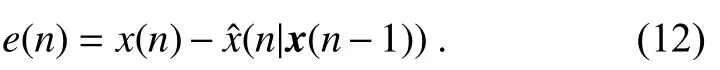
式(11)中,抽头权系数wk(n)通过LMS 算法进行多次迭代获取。LMS 算法是最速下降算法的随机实现,通过多次迭代趋近于维纳方差的最优解。系数迭代式为
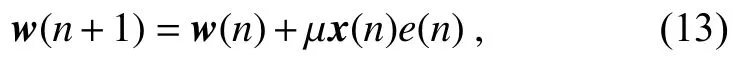
其中:µ是收敛系数,是人为设定的常量,收敛系数越大,收敛速度越快。为了保证迭代收敛,收敛系数需满足条件:

其中:λmax是输入向量自相关矩阵的最大特征值。LMS 作为一种迭代算法,其计算效率通常用收敛速度衡量。收敛速度是运行于平稳环境的线性自适应滤波算法收敛于维纳解所涉及代价的一个典型度量,其大小取决于其离散瞬态响应的时间常数,表示为

其中:λk是输入向量自相关矩阵的第k个特征值。在最差条件下,收敛速度将取决于最小特征值λmin,因此最小时间常数可以近似为
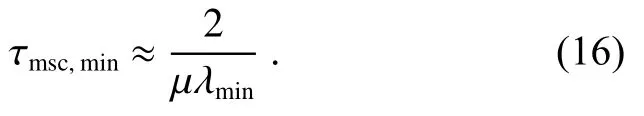
根据式(16),步长系数与LMS 算法的最小时间常数成反比关系,因此步长系数越大,LMS 的收敛速度越快。
设代价函数为误差函数e(n)的平方:

该算法稳态状态下与维纳滤波器的差距通过失调量来表征,定义为

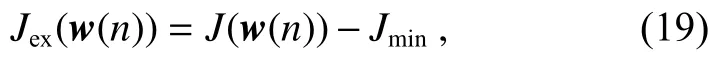
根据代价函数有:

假设n→∞时,LMS 前向预测器对输入的预测=u(n)。u(n)和v(n)分别是u(n)、v(n)的第n~(n−M+1)个数据组成的向量。误差函数的均方误差表示为

输出信号的信噪比表达为
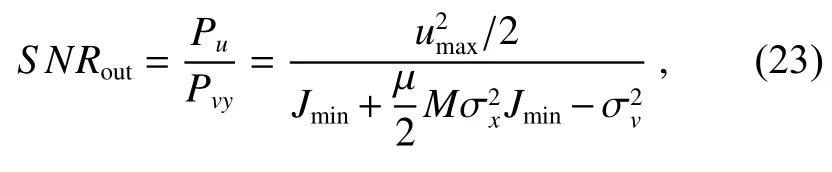
其中umax是振动速度信号的峰值。维纳滤波器在前向预测器应用中,预测误差的功率为信号内随机噪声的功率与滤波器未滤除噪声的叠加:
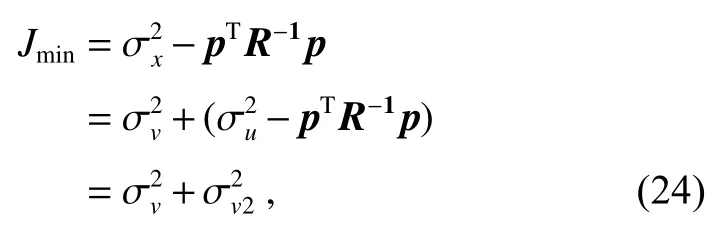
其中:p为输入向量x(n−1)与参考信号x(n)的互相关向量,R为输入向量x(n−1)的自相关矩阵。式(24)中的pTR−1p分量是维纳滤波器对速度信号u(n)的预测,可以归一化为
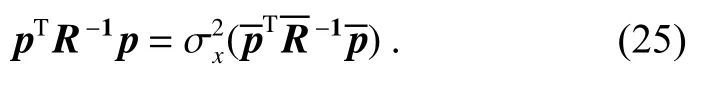
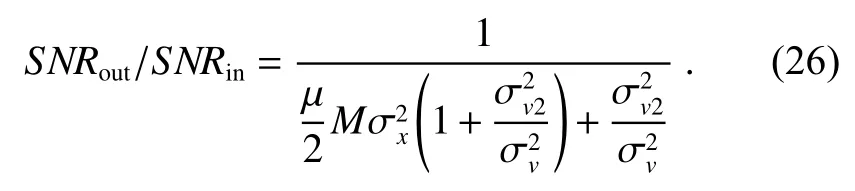
上式可以用来估计滤波器参数的取值:针对一个测量速度范围为0~Tm/s 的激光测振仪,若要输出信噪比至少为输入信噪比的X倍,则要满足条件:
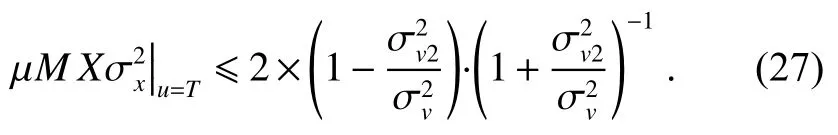

对于均值为0 且互不相关的噪声和振动速度信号,当振动速度信号是正弦信号时,输入信号方差为
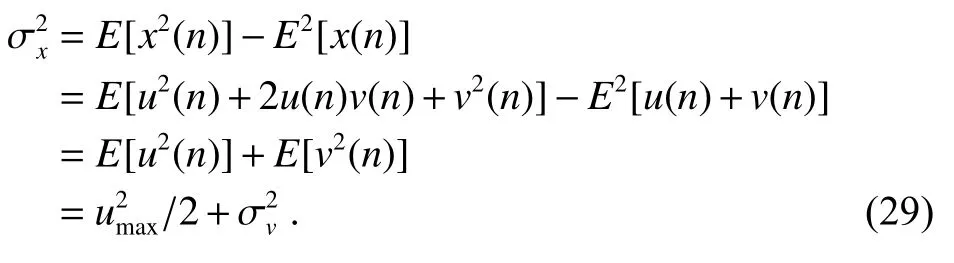
根据上述条件设计滤波器参数可在满足最低滤波信噪比的条件下获得最大的步长系数,从而降低LMS 前向预测器的响应时间。
3 仿真及结果分析
依据式(9)中的振动速度测量信号模型,构建仿真输入信号:
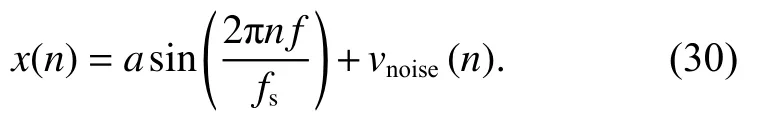
设定速度信号峰值a小于10 m/s,速度信号频率f的范围为0 ≤f<25 kHz。功率为−70 dBW 的白噪声经过图1 所示解调系统,输出噪声为vnoise(n)。将该振动速度信号作为LMS 前向预测器的仿真输入。
3.1 输入信号频率对滤波信噪比的影响仿真分析
设置输入信号峰值为1 m/s,LMS 前向预测器的采样频率200 kHz,步长系数µ=0.0002,阶数为100 阶。得到输入信号频率对滤波信噪比的影响如图3 所示。
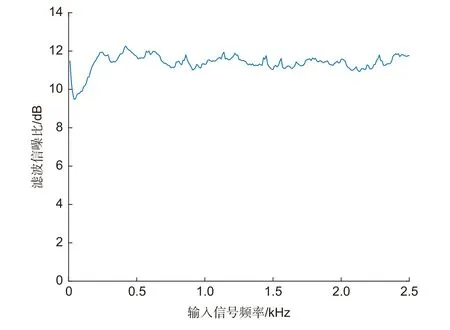
图3 输入信号频率对滤波信噪比的影响Fig.3 Influence of input signal frequency on filter SNR
图3 的结果表明,在输入信号峰值小于1 m/s,振动频率在0~25 kHz 的范围内时,滤波信噪比的波动小于2 dB,其中在频率为2 kHz~25 kHz 的范围内滤波信噪比的波动小于1 dB。自适应滤波器收敛完毕后,表现为中心频率与输入信号频率相同的滤波器,由于滤波器通带内噪声被保留,而通带内噪声的功率是随机分布的,导致输出信噪比也受噪声分布影响而出现波动。因此LMS 前向预测器的滤波信噪比受到输入信号频率的影响原因主要是噪声的功率谱分布不均,而非输入信号的频率变化影响所致。
3.2 输入信号峰值对滤波信噪比的影响仿真分析
设置采样率200 kHz,输入信号频率1 kHz,峰值范围0.01 m/s~10 m/s,步长系数µ=0.0002,阶数为100 阶,输入信号峰值对滤波信噪比的影响如图4所示。
根据图4,随着输入信号峰值的增加,滤波信噪比经历了缓慢下降的过程,符合式(26)的变化趋势。当输入信号峰值为10 m/s 时,滤波信噪比接近于0,满足步长系数取值的约束条件。滤波器抽头权系数的取值可以看作“凸优化问题”。在“凸优化问题”中,自适应滤波是次优算法:到达维纳最优点的邻域后,它将以随机游走的方式在最优点附近徘徊,从而无法停留在最优点上[17]。这种徘徊过程造成的与最优解的偏差产生了高斯分布的梯度噪声,由于失调代表了自适应滤波器在稳定状态下,与维纳最优解的偏差,所以噪声功率与失调正相关。因此需结合步长系数、阶数和输入信号峰值综合考虑滤波器的设计参数。
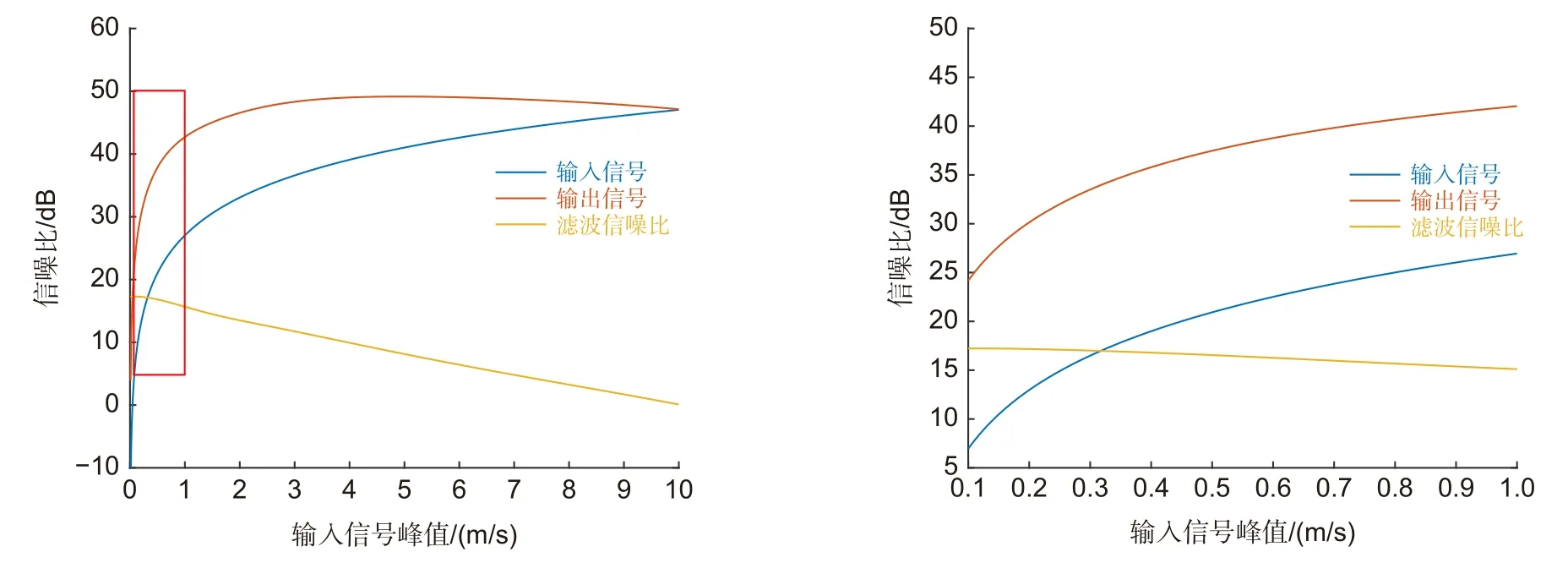
图4 输入信号峰值对滤波信噪比的影响Fig.4 Influence of input signal peak on filter SNR
3.3 步长系数对滤波信噪比的影响仿真分析
对LMS 前向预测器的步长系数与滤波信噪比之间的关系进行仿真分析。设置输入信号频率10 kHz,峰值1 m/s,LMS 前向预测器的采样频率200 kHz,阶数为100 阶,改变步长系数得到步长系数对滤波信噪比的影响如图5 所示。
根据图5,步长系数在0.000001~0.01 的范围内,滤波信噪比随步长系数的增加单调递减,符合式(26)中步长系数与滤波信噪比的反比例关系。当步长系数超过0.01 时,不满足式(14)的约束条件,会导致迭代过程不收敛,不探究其影响关系。
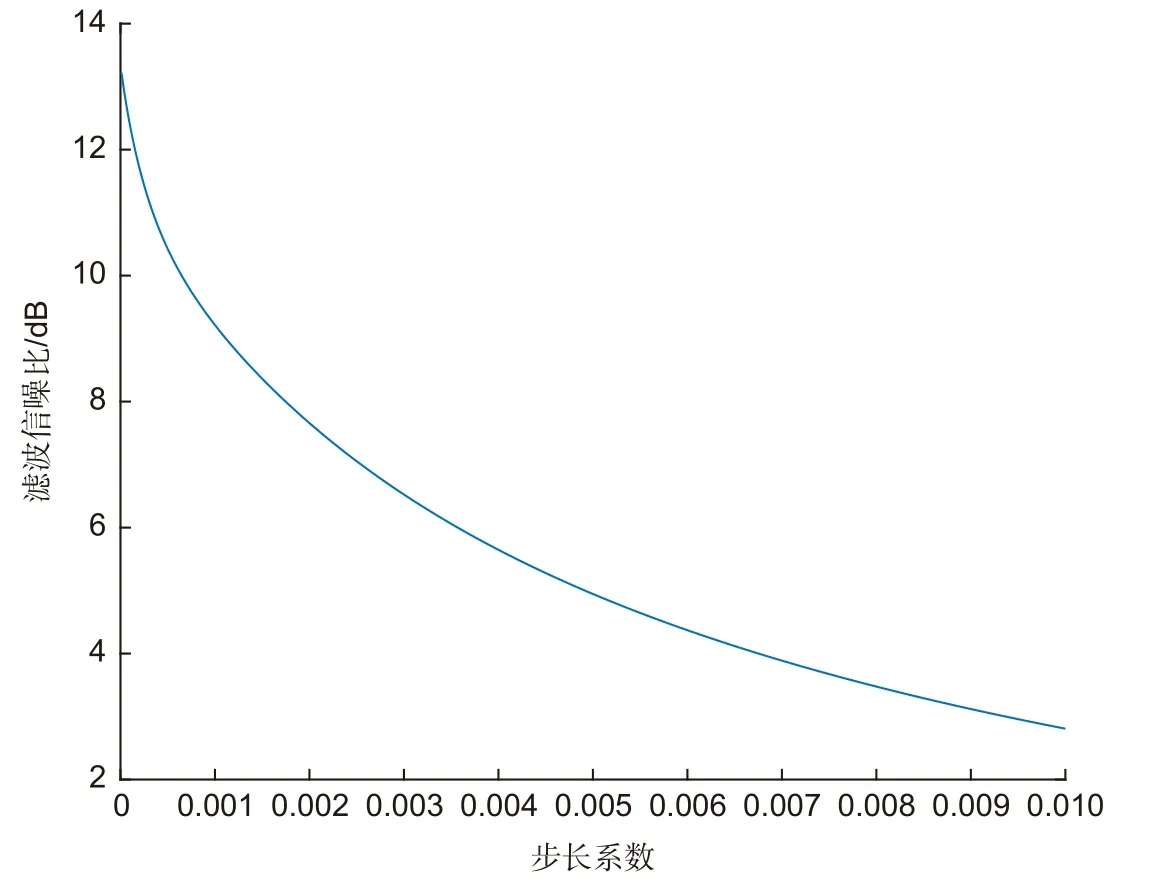
图5 步长系数对滤波信噪比的影响Fig.5 Influence of step size coefficient on filter SNR
3.4 阶数对滤波信噪比变化的影响仿真分析
对LMS 前向预测器的阶数与滤波信噪比之间的关系进行仿真分析。设置输入信号频率10 kHz,峰值1 m/s,LMS 前向预测器的采样频率200 kHz,步长系数为0.0002。改变滤波器阶数,得到阶数对滤波信噪比的影响如图6 所示。
根据图6,随着滤波器阶数增加,输出信噪比呈现先上升后缓降的趋势。这是由两方面因素共同影响的:一方面自适应滤波器作为维纳滤波器的迭代近似实现,根据维纳滤波器的多重线性回归模型,维纳滤波器的均方误差随阶数增加先减小后不变。而依据式(18),LMS 的失调随阶数增加而增大,即与维纳最优解的差距增大,导致引入了随阶数增加的梯度噪声。因此阶数增加时,输出信号信噪比并非呈单调递增关系。
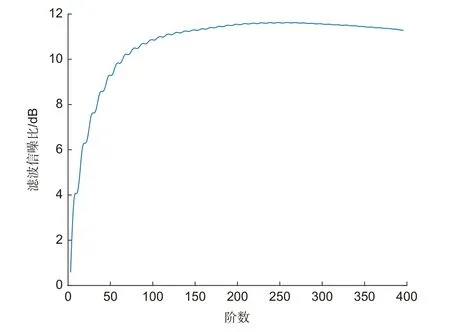
图6 阶数对滤波信噪比的影响Fig.6 The effect of order on filter signal-to-noise ratio
根据仿真结果,阶数小于100 阶时,随着阶数增加,滤波信噪比增长幅度较大;在100 阶~250 阶范围内滤波信噪比增长速度缓慢,只有0.77 dB 的增长。另外在FPGA 硬件实现LMS 前向预测器时,更高的阶数会带来更多的硬件资源占用并叠加更大的量化噪声。每增加1 阶,LMS 前向预测器的资源消耗增加1 个乘法器和2 个加法器,综合考虑资源消耗和阶数对滤波信噪比的影响,最终确定仿真阶数为100 阶。实际设计时需要结合失调、资源占用和量化噪声综合考虑阶数的选择。
3.5 输入信号信噪比对滤波信噪比变化的影响仿真分析
对输入信号噪声功率与滤波信噪比之间的关系进行仿真分析。设置输入信号频率10 kHz,LMS 前向预测器的采样频率200 kHz,阶数100 阶,步长系数为0.0002。保持输入信号功率0 dBW 不变,改变输入信号信噪比,得到输入信号信噪比对滤波信噪比的影响如图7 所示。
根据图7,输入信号信噪比大于−10 dB 时,滤波信噪比最大;当输入信号信噪比在小于−10 dB 时,LMS 前向预测器的滤波信噪比随输入信噪比的下降出现衰减,直至在−30 dB 处滤波信噪比变成0.12 dB。根据式(24)和式(26),在信噪比过小的情况下,LMS前向预测器对速度信号的预测功率远大于速度信号功率,造成未滤除噪声与输入信号噪声的功率比值变大到无法忽略,最终造成滤波信噪比降低。仿真表明,LMS 前向预测器在输入信号信噪比为−30 dB~70 dB 范围内具有滤波效果,其中在输入信号信噪比大于−10 dB 时滤波信噪比达到最优。
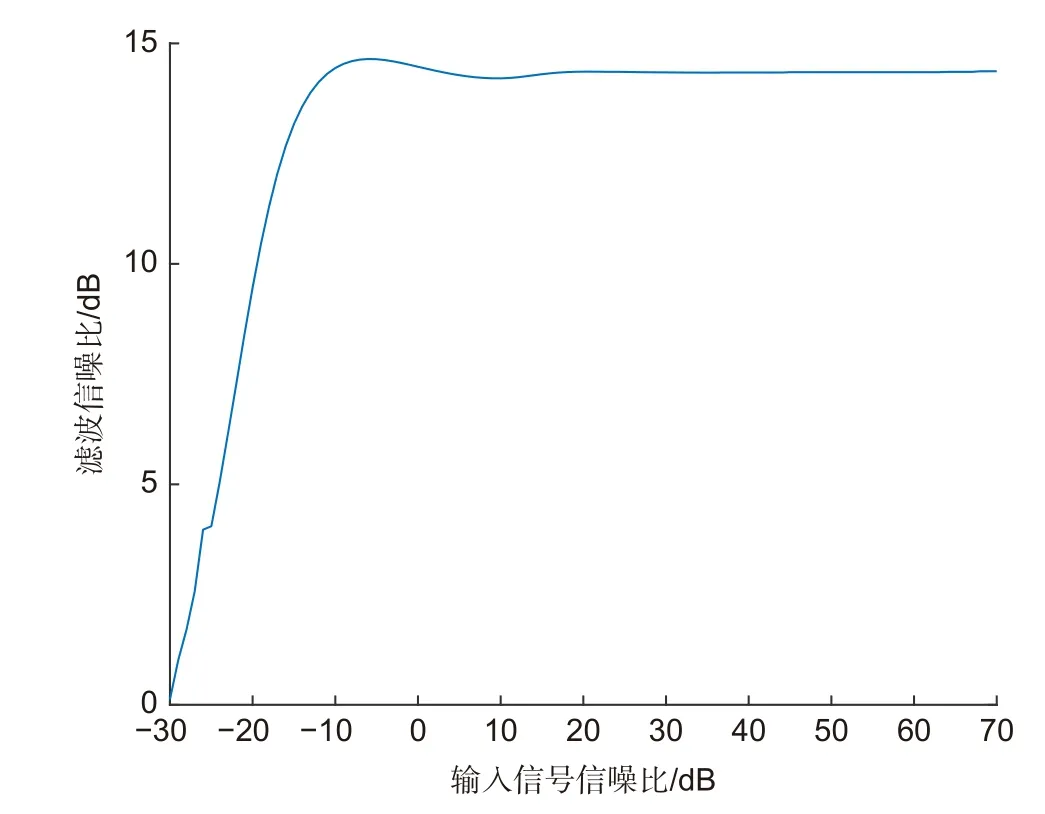
图7 输入信号信噪比对滤波信噪比的影响Fig.7 The impact of the input signal SNR on filter SNR
3.6 步长系数对收敛速度的影响仿真分析
对步长系数与收敛速度之间的关系进行仿真分析。设置输入信号频率10 kHz,峰值为1 m/s,LMS 前向预测器的采样频率200 kHz,阶数100,改变步长系数得到不同步长系数下LMS 前向预测器的学习曲线如图8 所示。
图8 反映了LMS 前向预测器的均方误差(e(n)2)与自适应循环次数的关系。根据图8,步长系数在0.000001~0.01 范围内,步长系数越大,均方误差到达稳定的循环次数越少,即LMS 前向预测器的收敛速度越快。设置更大的步长系数能提高滤波器的收敛速度,而更大的步长系数会造成滤波信噪比的衰减,所以需合理设计LMS 前向预测器的步长系数。采用式(28)对步长系数进行合理取值,可以在给定最小信噪比的条件下获得较快的收敛速度,以提高自适应滤波的算法迭代效率。
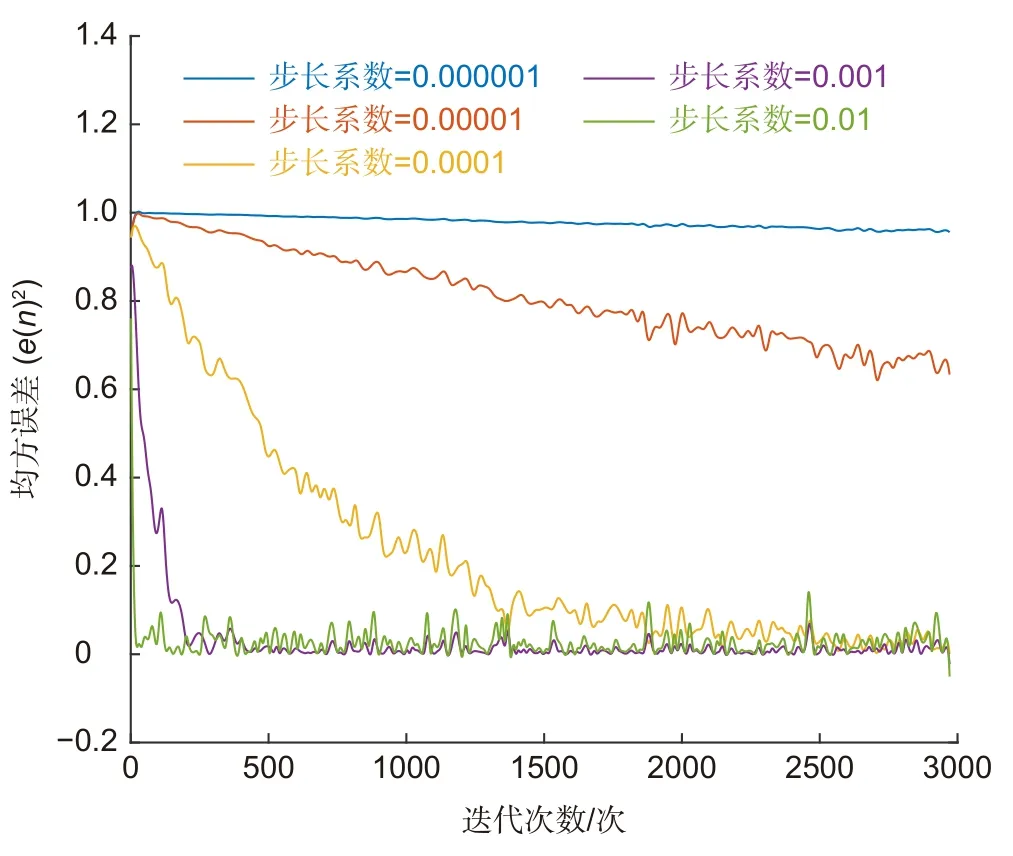
图8 不同步长系数下的学习曲线Fig.8 Learning curves under different length coefficients
4 实验验证
4.1 实验平台搭建
为了验证振动信号频率和峰值对LMS 前向预测器输出信噪比的影响,采用自研的激光测振仪和商用标准振动发生器搭建试验系统。实验在光学超净实验室进行,环境无明显振动。使用NTI 公司的Minirator型模拟音频信号发生器,控制TalkBox 型声学信号发生器产生单频振动。自研激光测振仪放置在声学信号发生器6 m 处,振动探测目标为扬声器振膜,将自研激光测振仪采集的振动探测数据传送至上位机进行正交解调处理,得到振动速度测量信号。将该信号作为LMS 前向预测器的输入,分别验证信号频率和峰值对滤波信噪比的影响。数据处理流程图如图9 所示。自研激光测振仪的激光波长为1550 nm,测量频率范围DC~25 kHz,采样率200 kHz。设置LMS 前向预测器阶数为100 阶,步长系数是0.0002。实验系统示意图和实物图如图10 所示。

图9 振动速度信号自适应滤波数据处理流程框图Fig.9 Block diagram of adaptive filtering data processing flow for vibration velocity signal
4.2 输入信号频率对滤波信噪比的影响验证
通过实验验证信号频率对LMS 前向预测器信噪比的影响。由于声学信号发生器的输出频率最大为10 kHz,所以在10 kHz 范围内产生振动速度信号,依次通过LMS 前向预测器进行滤波处理。其中频率为10 kHz 时,滤波前后振动信号的波形图和频谱图如图11 所示。
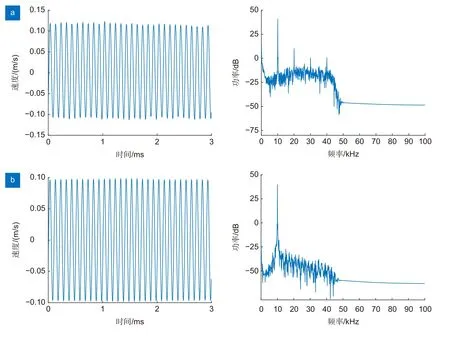
图11 滤波前后波形和频谱对比。(a) 滤波前波形和频谱图;(b) 滤波后波形和频谱图Fig.11 Waveform and spectrum comparison before and after filtering.(a) Waveform and spectrum diagram before filtering;(b) Waveform and spectrum diagram after filtering
改变振动频率,并通过调节信号发生器峰值来保持速度信号的峰值不变。得到输入信号频率与滤波信噪比的关系如图12 所示。
根据图12,频率变化造成滤波信噪比的偏差小于2 dB。由于每次采集数据相隔时间大约为5 min,在不同时段的采集过程中,环境振动不完全相同,影响了输入噪声的幅频特性,导致LMS 前向预测器收敛完毕后,通带内保留的噪声功率偏差增大,从而导致滤波信噪比的偏差增大。实验验证结果与3.1 节中输入信号频率对滤波信噪比影响的仿真结果基本一致。由于激光测振仪中速度测量信号的噪声近似高斯白噪声,待自适应收敛完成后,滤波器通带内保留的噪声功率变化较小,因此输入信号频率对LMS 前向预测器的滤波信噪比影响较小。
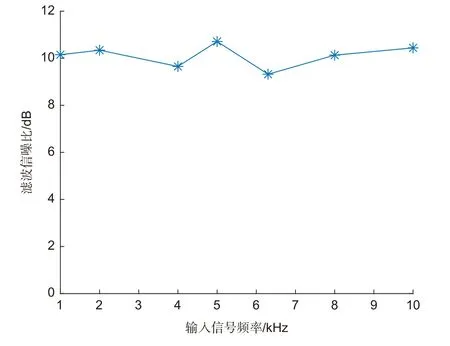
图12 输入信号频率与滤波信噪比关系的实验结果Fig.12 Experiment on the relation between input signal frequency and filter SNR
4.3 输入信号峰值对滤波信噪比的影响验证
通过实验验证振动测量信号峰值对LMS 前向预测器信噪比的影响。设置音频信号发生器频率10 kHz,通过改变音频信号发生器的输出正弦信号峰值,激励声学信号发生器振膜产生不同速度大小的振动,采用自研激光测振仪对振膜的振动进行探测。由于声学信号发生器振膜的振动速度较小,难以体现速度信号峰值对于滤波信噪比的影响,所以将解调出的速度信号进行数字放大,获得不同峰值的滤波器输入信号。取两个连续零点的中点为一个极值,多个极值点取平均值得到近似的输入信号峰值。输入信号峰值与滤波信噪比的关系如图13 所示。
根据图13,输入信号峰值越大,滤波信噪比越小。滤波信噪比和斜率与3.2 节仿真结果基本一致。由于自适应滤波器的输入信号峰值增加时,每次抽头权系数迭代的长度也随之增加,导致在“凸优化问题”中,抽头权系数距离最优解的距离方差增大,使得产生的梯度噪声增加,进而降低了滤波器的滤波信噪比。通过实验验证了0.1 m/s~1 m/s 范围内输入信号峰值对滤波信噪比的影响关系,为LMS 前向预测器适应的振动测量速度范围提供依据。
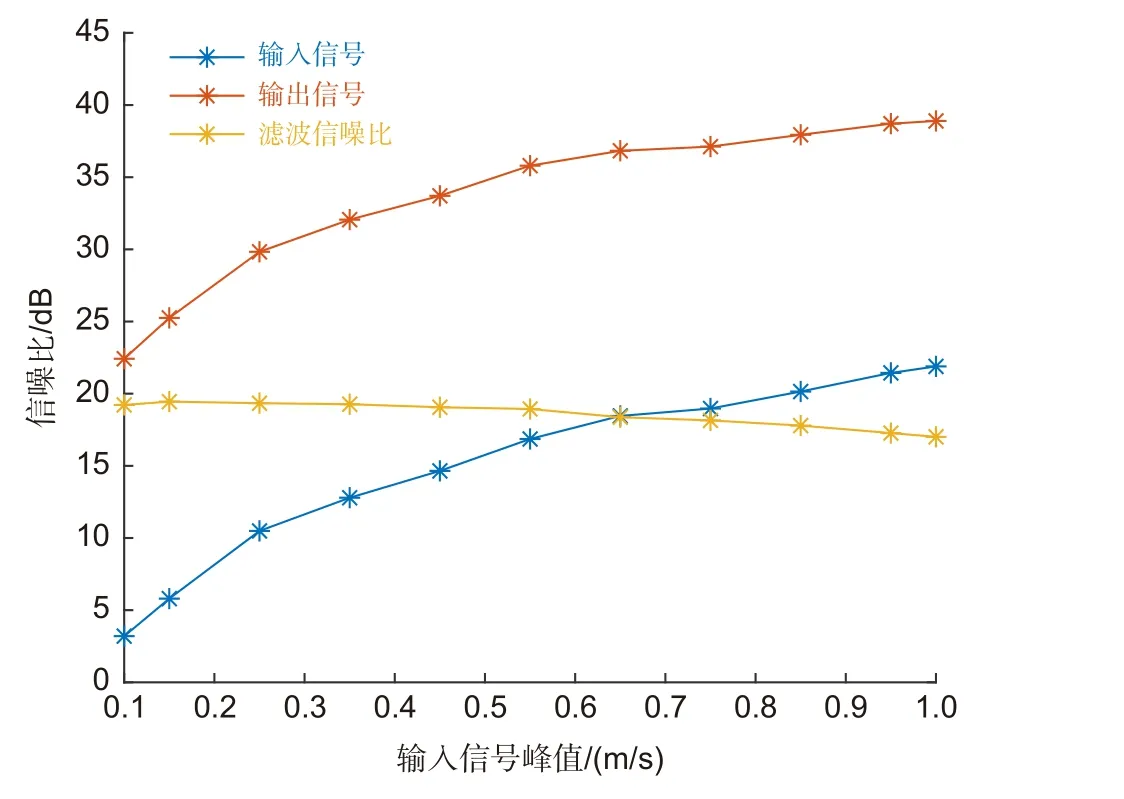
图13 输入信号峰值与滤波信噪比关系的实验结果Fig.13 Experiment on the relationship between input signal peak value and filter SNR
5 结论
本文采用LMS 前向预测器实现了激光测振仪的自适应滤波功能,并分析了影响LMS 前向预测器信噪比和响应时间的因素。仿真和实验表明,可以作为实现激光测振仪自适应滤波的一种途径,适用于建筑物振动检测、机械振动测量、材料表面微小损伤检测等应用的振动速度信号滤波。LMS 前向预测器的滤波效果和收敛速度受到输入信号峰值、阶数和步长系数的影响,可以结合系统对最小滤波信噪比和振动速度测量范围的需求对滤波器参数进行选择和设计。本文为LMS 前向预测器的参数选择提供了理论依据,为设计适用于激光测振仪自适应滤波器提供技术手段。

