同偏振记录偏光全息的零再现
林阿愿,王瑾瑜,陈宇昕,齐沛良,黄志云,谭小地*
1 福建师范大学光电与信息工程学院,信息光子学研究中心,福建 福州 350117;
2福建师范大学医学光电科学与技术教育部重点实验室,福建省光子技术重点实验室,福建省光电传感应用工程技术研究中心,福建 福州 350117
1 引言
光学全息术是利用感光材料记录物体光波和参考光波的干涉图样,在一定的条件下,利用光的衍射现象,通过参考光波照射干涉图样重建出原物体光波[1]。如今,全息技术不仅可以用于数字图像显示[2],也可以用于干涉计量[3]、光存储[4-5]和光学元器件制造[6]等领域。要说明的是,现在广泛应用的全息是所谓的强度全息,使用的是对偏振不敏感的材料,只记录了光场的振幅和相位信息。
1974 年,Kakichashvili 在对偏振敏感的各向异性材料中记录了光场的偏振信息[7]。1984 年,Nikolova和Todorov 提出用琼斯矩阵来表达再现光场的偏振态,在傍轴近似下(记录角度小于10°),很好地描述了偏光全息的再现现象[8]。2011 年,Kuroda 提出了一种新的基于张量方法的偏光全息理论[9]。该理论不仅能够描述任意记录角度下全息图的再现结果,并且在小角度下得到的结果与琼斯理论的一致。因此,张量偏光全息理论相比于之前的理论更为全面。如今,基于张量偏光全息理论的理论探究和实际应用取得了许多成果[10-14]。
众所周知,光场中包含了振幅、相位和偏振信息。相比于强度全息,偏光全息由于所使用的材料能对偏振产生响应,因此不仅可以记录光场的振幅和相位信息,还可以记录偏振信息。从这个角度看,偏光全息才是真正意义的“全息”。在强度全息的记录阶段中,一对偏振态正交的信号光和参考光是看不到干涉图样的。只有当二者的偏振态中能正交分解出相同的偏振分量,才会有干涉图样的产生。故可认为在强度全息的记录阶段中,信号光和参考光的偏振态是一致的;读取阶段中,在满足布拉格条件的情况下,即使用功率很低的读取光照射全息图时,也会产生再现光,并且再现光的偏振态总是与读取光保持一致。本文基于张量偏光全息理论,推导了相同椭圆偏振态记录的偏光全息的再现光场。结果表明,在特定条件下,即使布拉格条件满足,使用相同椭圆偏振态记录的偏光全息也会出现读取光功率不为零而再现光功率为零的现象,即所谓的零再现[15-16]。根据理论分析,设计了相应的零再现验证实验,结果与理论吻合得很好。
2 理论推导
偏光全息的记录阶段和再现阶段如图1 所示。

图1 非对称入射的偏光全息示意图。(a)记录阶段;(b)再现阶段Fig.1 (a) Recording stage and (b) reconstructing stage of polarization holography with asymmetric incidence
G+和G−分别表示信号光和参考光,GF表示再现光,F是读取光。θ±代表着信号光或参考光在材料中与z轴的夹角。在记录阶段中,信号光与参考光照射到材料表面,二者的耦合光场与材料相互作用,这样信号光就被记录在材料中。在读取阶段,用一束满足布拉格条件的读取光照射材料上被曝光过的位置,便能产生一束再现光。信号光与再现光的传播方向是相同的。根据张量偏光全息理论,可以将再现光的偏振态写为[9]

其中:

α和β分别是材料介电张量的标量部分和张量部分的系数,k+是信号光的光矢量,上标*表示共轭,下标+和-分别对应着信号光和参考光。记录过程中的信号光和参考光偏振态是相同的,因此将信号光、参考光和读取光设为

s是s 偏振光的单位向量,p±是p 偏振光的单位向量。其中系数f、j代表着信号光和参考光中的p 分量和s分量的振幅;b和q代表着读取光中的p 分量和s 分量的振幅。δ和γ表示s 分量和p 分量之间的相位差。为了简化书写,下面设:

将式(2)~式(6)代入式(1),经过化简可得:
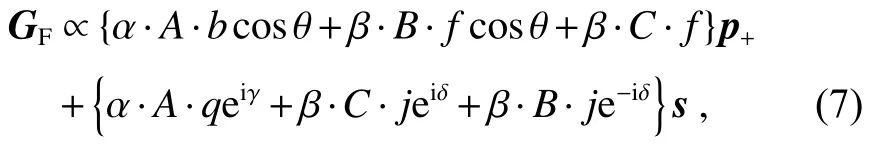
其中:θ=θ++θ−,表示记录角度。为了实现零再现,p+和s的系数需要同时等于零,此时可得:
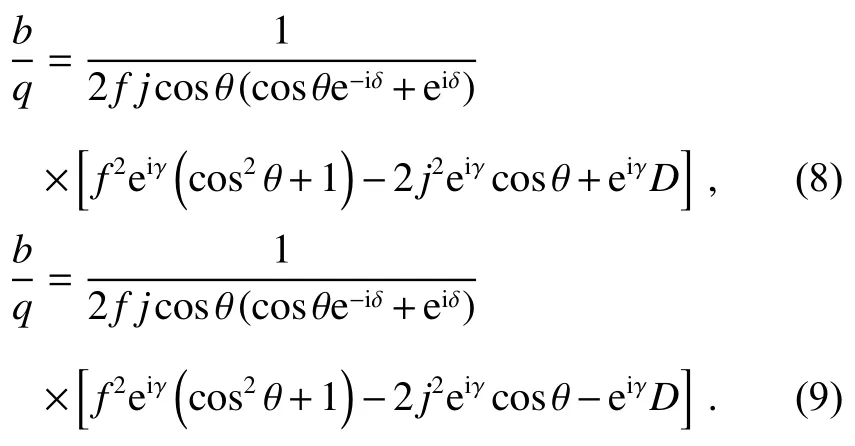
式(8)和式(9)表明,对于给定的信号光、参考光以及记录角度,有两束不同的读取光可以满足实现零再现的条件。将任意一个b/q值代回式(7)之后,便能得到此b/q值所对应的α/β。因此,不同的读取光所需的α/β值不同。
3 实验结果与讨论分析
实验中以掺杂菲醌的聚甲基丙烯酸甲酯(PQ/PMMA)[17]为记录材料。这是一种光致聚合物材料,在波长532 nm 处的折射率约为1.51[18]。先前的研究表明,本实验室自制的材料初始α/β约为8[19]。为了获得具有一般性的结果,在实验中采用椭圆偏振光。基于上述的理论推导,获得了一组能够实现零再现的实验参数,如表1 所示。
在表1 中,信号光、参考光和读取光都是标准椭圆偏振光。标准椭圆偏振光表示其长轴与水平方向平行或者垂直,这意味着p 分量和s 分量之间的相位差大小为π/2。除此之外,为了满足计算结果对记录角度的要求,图1 中记录角度被画成钝角。之所以采取非对称入射的方式来记录全息图,是因为材料表面较为光滑,读取光也会被材料表面所反射,造成再现光与被反射的读取光混合到一起。因此在记录阶段中,信号光入射角θ+与参考光入射角θ−不能相等。虽然θ+与θ−相差只有2°,但是材料到功率计之间还有60 cm左右的距离,足以将再现光和被材料表面反射的读取光分离开来。实验光路示意图如图2 所示。

图2 实验光路示意图。M:反射镜;HWP:半波片;QWP:四分之一波片;PBS:偏振分束棱镜;SH:电子快门;PM:功率计;PQ/PMMA:记录材料Fig.2 Schematic diagram of experiment about null reconstruction.M:mirror;HWP:half wave plate;QWP:quarter wave plate;PBS:polarization beam splitter;SH:shutter;PM:power meter;PQ/PMMA:recording material.
实验中的光源是波长为532 nm 的绿色激光。扩束整形后的激光依次通过HWP1 和PBS,得到功率各为52 mW 的s 线偏振光和p 线偏振光,以得到最佳的记录效果。利用半波片和四分之一波片能够获得任意的椭圆偏振光。HWP3 和QWP2 所在的光路作为信号光路;HWP2 和QWP1 所在的光路作为参考光路或读取光路。这两路光将光致聚合物材料PQ/PMMA 夹在中间,分别从材料不同的表面入射。读取光照亮材料中的全息图,PM 用来观察和记录再现光的功率变化。SH 用于记录阶段和读取阶段之间的切换。为了产生表1 中所需的偏振态,各个波片快轴所在的方位角设置参数如表2。
实验过程如图3 所示。

图3 实验流程图Fig.3 Experimental flow chart
实验采取边记录边读取的方式,因为如果一直处于记录阶段,就无法在实验过程中观察记录材料对偏振干涉光场的响应效果和全息光栅的质量。记录阶段持续5 s,在此期间打开SH1、SH2,关闭SH3;读取阶段持续0.5 s,在这期间需要打开SH1、SH3,关闭SH2。如此短的读取过程对全息光栅的影响可以忽略[20-21]。由表1 和表2 可知,HWP2 快轴角度在记录阶段和参考阶段是不一样的,故将HWP2 放置在电动位移旋转台上并由LabView 程序控制,以实现对其快轴所处角度的精确控制。实验结果如图4 所示。

表1 实验参数Table 1 Experimental parameters

表2 波片快轴与水平方向的夹角Table 2 Angle between fast axis and horizontal direction of wave plate
如图4 所示,随着曝光时间的增加,虽然再现光的功率一直在上升,但是功率一直处于较小值且不为零。实验中环境杂散光的功率在45 nW 左右浮动。理论上说,当用满足零再现条件的偏振态进行读取时,再现光的功率应为零,当然这在实际情况下是不可能的。但是根据表1 中的结果,当用其它偏振态的光读取时,都不能得到零再现,也就意味着再现光功率将会增大。因此,为了进一步确认是否已实现了零再现,在上述实验结束后,又进行了一次读取过程。在此过程中,让HWP2 的快轴旋转一圈,QWP1 的快轴保持在90°不变。此时任意的标准椭圆偏振光将照射在材料上而产生再现光。观察此过程中的功率变化情况,实验结果如图5 所示。

图4 再现光的功率随曝光时间的增加而变化Fig.4 Power of reconstructed wave varying with exposure time
图5 的结果表明,再现光功率随HWP2 快轴方位角的改变呈现周期性的变化,最大功率为130 μW左右。与图4 的实验结果相比,用其它偏振态进行读取时,再现光功率上升幅度十分明显。由前面的理论推导可知,零再现与读取光的偏振态有关,而且读取光的偏振态与理论值1.47p−+is越接近,其再现光的功率将越低。根据半波片的工作原理,理论上当HWP2 快轴方位角为−17.2°、72.8°、162.8°和252.8°时,此时HWP2 和QWP1 组合产生的椭圆偏振光的偏振态都是1.47p−+is。图5 中再现光功率处于极低值时所对应的快轴方位角分别是−17.2°、73.6°、161.7°和251°。综上所述,虽然用偏振态为1.47p−+is的光进行读取时再现光功率不为零且一直上升,但是此时的功率相比于用其他偏振态读取时的功率是非常微弱的,而且实验中功率极低值所对应的快轴方位角与理论值是非常接近的,因此可以认为实现了零再现。

图5 再现光的功率随HWP2 方位角改变的变化情况Fig.5 Power of reconstructed wave varying with azimuth of HWP2
4 结论
研究了大角度记录下用相同偏振光记录偏光全息的零再现现象。记录阶段的信号光和参考光是一对偏振态相同的椭圆偏振光,两者在材料内部的夹角约为136°。在读取阶段中,用理论计算所得的偏振态照射全息图时,再现光的功率非常微弱;用其他偏振态进行读取时,再现光的功率与前者相比最大可上升将近37 倍。本文验证了张量偏光全息理论的预测,给出了实现同偏振态记录偏光全息的零再现的条件。

