函数中的双变量问题探析
西华师范大学数学与信息学院 (637000) 王小梅 汤 强
双变量问题在近几年高考中的考察呈上升趋势,因其涉及知识点多,解法灵活,命题人往往在知识的交汇处进行命题,双变量问题便成为高考中的一个热点问题,同时,也是学生学习的一个难点,因此,有必要对双变量问题进行深入分析.目前,关于双变量问题的研究主要从解题策略方面进行,由于双变量问题涉及面广,解题策略一般具有普遍性,导致思想方法容易理解,但是应用起来很困难.因此本文从题型的角度分析双变量问题,另外,将思想方法渗透在解决问题过程中,旨在帮助学生快速识别题型,精准定位,选择合适的方法解决问题,达到高效解决函数中双变量问题的目的.
一、双变量问题的基本模型
双变量问题指的是题目中含有两个变量的问题,基本模型有两种(表达式中可含参):F(x1)≥G(x2)或F(x1)=G(x2)、F(x1,x2)≥0或F(x1,x2)=0.第一种模型为可分离的双变量问题,两个变量是独立的;第二种模型为藕合的双变量问题,两个变量藕合在一起,不可分离.
二、双变量问题的常见题型
对题型的整理有助于我们快速找到解决问题的突破口,函数中的双变量问题可以看成是单变量问题的延伸与拓展,常见的题型有如下四种.
(一)双变量之“存在性”、“任意性”问题
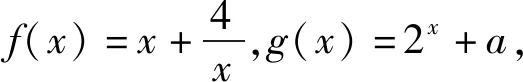
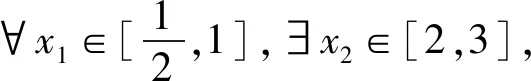
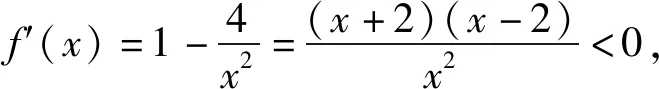
评注:该题的关键是将“存在性”、“任意性”问题转化为两个函数值域(或最值)之间的问题,另外,“存在”、“任意”可相互转化,共有以下四种情况:
记I1,I2分别为函数f(x)与g(x)定义域的子空间,A,B分别为函数f(x)在定义域I1上的值域与函数g(x)在定义域I2上的值域.
(1)∀x1∈I1,∀x2∈I2,f(x1)≥g(x2)⟹[f(x)]min≥[g(x)]max;
(2)∀x1∈I1,∃x2∈I2,f(x1)≥g(x2)⟹[f(x)]min≥[g(x)]min;
(3)∃x1∈I1,∀x2∈I2,f(x1)≥g(x2)⟹[f(x)]max≥[g(x)]max;
(4)∃x1∈I1,∃x2∈I2,f(x1)≥g(x2)⟹[f(x)]max≥[g(x)]min.
除此之外,若将不等式改为等式,则有以下四种情况:
(5)∀x1∈I1,∀x2∈I2,f(x1)=g(x2)⟹A=B;
(6)∀x1∈I1,∃x2∈I2,f(x1)=g(x2)⟹A⊆B;
(7)∃x1∈I1,∀x2∈I2,f(x1)=g(x2)⟹A⊇B;
(8)∃x1∈I1,∃x2∈I2,f(x1)=g(x2)⟹A∩B≠φ.
关于具体的例子文[1]已对含有参数的方程(或不等式) 中的“任意性”与“存在性”问题进行梳理,并用例子加以解释,指出破解此类问题的关键在于将其转化为熟悉的基本初等函数的值域问题,同时还需要正确区分“任意性”与“存在性”问题.
(二)双变量之极值点偏移问题
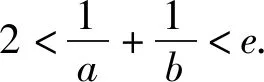
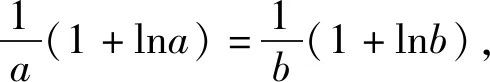
解:(1)对f(x)求导后分析其单调性,可得f(x)在(0,1)上单调递增,(1,+∞)上单调递减.
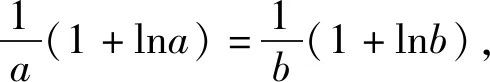
先证2

评注:极值点偏移问题是近几年高中解题研究的一个热点,对于此类问题的研究比较成熟,有固定的解题程序,文[2]提出了极值点偏移的概念与解决此类问题的通法,通过构造一元对称差函数,利用函数单调性解决,文[3]将极值点偏移问题进行了拓展,提出了非常规的极值点偏移问题的4种解决策略:构造差函数法、等量代换法、换元法、不等式放缩法.其实,我们将视野放大一些,可将极值点问题看成双变量问题的一个分支,解决此类问题的关键在于如何将双变量化为单变量,从而,非常规的极值点偏移问题的解决策略就很容易理解了.
(三)双变量之方程问题
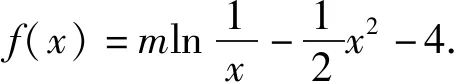
(1)讨论函数f(x)在(2,+∞)上的单调性;
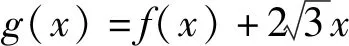
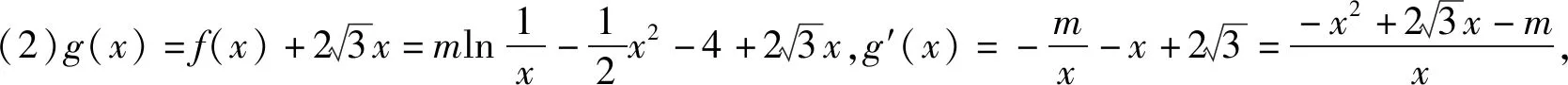
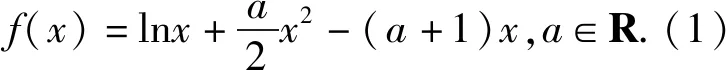

评注:不难发现,这类题的共性是存在等量关系,通过对条件进行化简,可以得到关于x1,x2的二元方程,利用韦达定理可实现消元,条件通常用零点、极值点、导数相等加以包装,若两个变量可分离,则用一个变量代替另一个变量实现消元,若两变量不可分离,则结合问题通过换元法实现消元(包括整体换元、引参换元).
(四)双变量之“对称”不等式问题
函数中的双变量问题还有一类题比较典型且有法可依,即对称型的不等式问题,其结构对称,两个变量独立且可分离,这时,构造函数法不失为一种简单高效的方法.
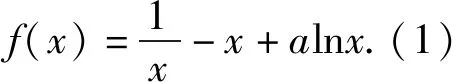
分析:第二问可从两个角度进行分析,一是代数式的结构特征,容易看出该不等式结构对称,且两个变量相互独立,将其变形可利用构造函数结合函数的单调性解决;二是条件中涉及极值点,可得到极值点x1,x2之间的等量关系,再利用消元法或换元法将双变量变为单变量问题.
解:(1)略;(2)思路1:(构造函数法)不妨设x1>x2>0,对结论进行变形得f(x1)-(a-2)x1 变式(2021年4月马鞍山二模,21题)已知函数f(x)=xlnx-ax2+(2a-1)x+a,其中a为常数. 分析:第(2)问,从式子的结构入手,和例2类似,将其变形可化为独立的双变量问题,再通过构造函数将独立的双变量问题化为单变量问题. 评注:通过例3可以看出思路1要比思路2和3简单许多,运算量较小,因此我们可以直接从式子的结构特征入手,遇到上述这种“对称”型不等式时,可采用构造函数进行消元,前提是两个变量独立可分离的.通常采用的解题步骤是:首先,观察代数式的结构特征,对代数式进行简单的数学运算;其次,将代数式两边的结构一致化,构造新的函数;最后,利用函数的单调性解不等式.其中最为关键的是识别代数式的结构特征,构造新函数. 通过上述分析,双变量问题涉及面广,考察学生对知识的灵活应用,但是不管怎么变化,解决此类问题的思想方法不变.从宏观的角度,解决双变量问题的两大思想为消元和化归思想,将不熟悉的问题化为熟悉的问题,其实,消元的目的也是将复杂的二元问题化为一元问题,关键在于如何消元将双变量转化为单变量. 从微观解题方法来说,主要方法有:构造函数法、消元法及换元法.构造函数常见于“对称型”不等式中,通过构造函数利用函数单调性解决;代入消元一般在含有等量关系时使用,常见于含有极值点的问题中,令导函数等于0,化简后一般为一元二次方程,可利用韦达定理实现消元;换元法包括整体换元(比值换元、差值换元、乘积换元等)、引入参数换元,值得注意的是,换元后自变量的范围有所改变.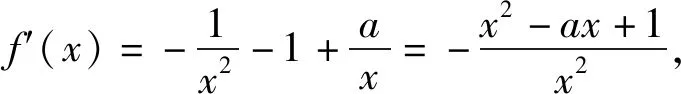
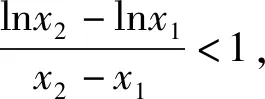

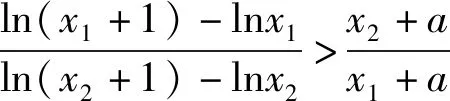
三、双变量问题的思想方法

