裂变产额的Zp模型评价方法及燃耗不确定度分析

舒能川，朱淑瑜，祖铁军，金永利，卢泽润，曹超维，宿 阳，刘丽乐，陈永静，葛智刚，刘 萍，黄小龙，续瑞瑞

(1.中国原子能科学研究院 核数据重点实验室，中国核数据中心，北京 102413；2.西安交通大学 核科学与技术学院，陕西 西安 710049)

裂变产额在核科学技术和核工程中有着重要的作用，可应用于燃耗计算、爆炸威力确定、衰变热计算、裂变缓发光子谱计算等[1-3]。在基础领域，用于裂变机制验证，同时也是天体演化过程的基础数据，用于元素核合成的计算[2]。

产额数据库的研制包括：1) 产额评价，通过实验数据收集和分析，获得可靠的产额和合理的误差，利用模型计算获得实验缺失数据；2) 产额建库，进行库格式及物理检验并燃耗计算分析，确保产额数据的合理性和可靠性；3) 提供用户使用，收集用户反馈意见，为后续更新评价提供参考。

传统产额评价方法[4-5]，通常是针对某一特定产物核，未考虑同一条质量链上其他产额的物理相关性，给出产额不一定自洽。为了解决这个问题，需要选择合适的模型对独立产额和累积产额进行统一描述，获得自洽的产额结果。

系统学模型和唯象模型可较好地描述裂变产额[6]，如Wahl的系统学计算程序CYF[7]，Schmidt的唯象模型计算程序GEF[8]以及中国原子能科学研究院发展的半经验模型[9]。这些模型的核心是基于裂变多模式和电荷近似高斯分布(Zp模型)的物理思想。对同一参数，不同程序存在着差异。其中分布宽度参数总体来说比较一致，分布于0.5～0.6左右，适用于预测未知产额，但由于具体数值相差20%，对于精确描述产额存在一定困难。

本工作目的是发展Zp模型，使之适用于独立产额和累积产额的统一描述，为产额评价建库提供技术支撑，并通过燃耗计算中响应量的不确定度分析，分析产额数据库的可靠性。

1 基于Zp模型的裂变产额统一评价方法

首先对实验数据收集、修正，作为模型拟合的数据基础；然后利用最小二乘法拟合实验数据，获得模型优化参数；最后通过模型计算，获得自洽的独立产额和累积产额及相应的协方差数据。主要流程如图1所示。

图1 裂变产额统一评价流程示意图Fig.1 Flow chart of unified evaluation of fission yield

1.1 实验数据基础

实验数据主要来自国际原子能机构的EXFOR(exchange format)实验数据库[10]，包括累积产额、独立产额和链产额。根据实验具体信息对其进行取舍，如数据陈旧、实验测量或数据处理中有错漏、与其他的数据分歧比较大而无详细信息。对于相对测量产额，用已评价的标准产额进行转换。

实验数据误差决定了该数据在评价过程中的权重，不合理误差需要调整，表1列出不同条件下的误差信息[11]。

表1 不同条件下产额测量的估计误差Table 1 Assumed errors for difference measurement cases

对于用相对测量方法得到的产额，需要用最新的标准产额对其进行修正：

(1)

式中：Y0为实验原测量值；YS0为实验中所用标准产额；YS为最新评价过的标准产额；Y为修正后的产额。对于直接γ法测量数据，需用新的分支比对其进行修正：

(2)

式中，I0、I分别为γ强度和新的强度。修正后产额误差按照误差传递方式得到。

1.2 Zp模型

对于给定质量数A，产额的电荷分布即独立产额YI可以用近似高斯分布叠加奇偶效应来描述[6-7]:

NA·[erf(V)-erf(W)]

(3)

(4)

(5)

(6)

(7)

(8)

式中：ZF、AF分别为复合核的电荷数和质量数；σ为分布宽度；Zp为最可几电荷，根据电荷不变原理，再加上一个修正电荷极化因子ΔZp；F(Z,A)为中子奇偶效应FN和质子奇偶效应FZ的乘积或倒数的乘积；erf为误差函数；NA为归一化参数，使得独立产额之和(扣除衰变到其他链的份额后)等于链产额。链上的累积产额为各先驱核及本身独立产额对该核的贡献，即：

YC=MIC×YI

(9)

式中：YI、YC分别为独立产额和累积产额组成的1×N维矩阵，N为产物核的个数；MIC=(ri,j)，为独立产额到累积产额的N×N维转换矩阵，矩阵元ri,j为产物核i的独立产额对j核的贡献，对角元为自身贡献，非对角元可以根据衰变分支比计算得到。

上述模型有5个参数，即NA、ΔZp、FZ、FN、σ，采用最小二乘法[12]拟合实验数据得到优化参数。图2示出CYF、GEF模型使用的热中子诱发235U裂变独立产额的分布宽度。

图2 CYF和GEF模型独立产额分布宽度Fig.2 Independent fission yield distribution widths from CYF and GEF codes

2 235U热中子独立产额不确定度计算方法

裂变产额是反应堆燃耗计算输入参数，产额不确定度通过燃耗计算传递给原子核密度、特征值等宏观响应量。西安交通大学基于广义微扰理论自主开发的燃耗计算不确定度计算程序NECP-SUNDEW[13-15]可求解特征值和原子核密度等宏观响应量对核数据相对灵敏度系数。

2.1 理论模型

广义微扰方法量化不确定度首先要计算响应参数对输入参数的相对灵敏度系数，然后基于相对灵敏度系数和输入参数的协方差数据采用“三明治法则”计算不确定度[16]：

(10)

式中：SD(R)为响应参数的相对不确定度；Sσ为响应参数R对于核数据σ的相对灵敏度系数矩阵；COVσ为核数据σ的相对协方差矩阵。

2.2 燃耗灵敏度计算方法

关于输入参数σ的响应参数R，其相对灵敏度系数定义为：σ的变化造成响应参数R的相对变化量。tf时刻，R对在t0时刻发生扰动的变量σ的相对灵敏度系数S的表达式为:

(11)

在核反应堆物理计算中，R可表示为：

R=f[σ,N(r,t),Φ(r,E,Ω,t),Φ*(r,E,Ω,t)]

(12)

式中：N(r,t)为原子核密度；Φ(r,E,Ω,t)为中子角通量密度；Φ*(r,E,Ω,t)为共轭中子通量密度；r为位置；E为能量；Ω为角度；t为时间。将式(11)关于核数据σ进行1阶泰勒展开可得：

(13)

式中：t0为燃耗的起始时刻；tf为结束时刻。式(13)第1项是灵敏度系数的直接项，是由核数据的变化直接引起的响应参数的变化；后3项是间接影响项，是由核数据的变化引起各核素的原子核密度、中子通量密度、共轭中子通量密度的变化，并最终造成响应参数的变化。由式(13)可知，求解灵敏度系数S需给出中子通量密度Φ、共轭中子通量密度Φ*及原子核密度N对于核数据的微分。

NECP-SUNDEW采用广义微扰理论对式(13)进行求解，该程序最初版本仅进行燃耗计算对核截面的不确定度分析[14]，文献[15-16]将该程序扩展到裂变产额、衰变常量等数据。具体的求解过程可参见文献[15-16]，本文直接给出宏观响应对裂变产额数据相对灵敏度系数的计算公式：

(14)

式中：I为燃耗总步数；N*为共轭原子核密度；A为燃耗方程的转换矩阵。

2.3 裂变产额协方差计算方法

具有相同质量数的若干裂变产物组成1条质量链，直接使用独立产额不确定度数据进行响应量的不确定度计算，就忽视了1条质量链上独立产额的相关性，会明显高估裂变产额引入的不确定度。NECP-SUNDEW程序采用Katakura[17]建立的最小二乘法计算独立产额协方差矩阵，可考虑同一质量链中各独立产额的相关性。独立产额协方差矩阵的对角线元素μii和非对角线元素μij分别为：

(15)

(16)

式中：Δyi为独立产额yi的不确定度；j表示同一质量链中各裂变产物；ΔY为质量产额的不确定度，通过下式计算：

ΔY=RYM

(17)

式中：RY为1条质量链的相对不确定度，从文献[18]中读取；M为1条质量链的质量产额。

为降低计算成本，NECP-SUNDEW程序采用包含195个裂变产物核素的压缩燃耗链进行计算。通过式(15)和(16)得到的协方差矩阵包含评价库内的所有裂变产物核素，因此要将该协方差矩阵进行压缩，使矩阵内的核素与程序燃耗链内的核素相一致。

3 裂变产额评价

本文以热中子诱发235U裂变A=125质量链裂变产物产额为例，说明评价过程。

质量数A=125的衰变链如图3所示，包括了β-衰变和IT退激，箭头中的数字表示分支比(%)，缺省的为100%。相应独立产额至累积产额的转换矩阵列于表2(i核到j核的贡献)。

表2 A=125衰变链的转换矩阵元Table 2 Conversion matrix element for decay chain of A=125

图3 A=125的衰变链Fig.3 Decay chain of A=125

通过EXFOR收集到的A=125质量链裂变产额的实验数并采用35个实验点，经过γ分支比和标准产额修正，如图4所示，数据来自文献[19-34]和内部报告(图中标记为YAN.21、STE.51)。从图4可看出，BAI.09[20]的产额偏高，该实验数据采用质谱法确定产物核质量得到，质量分辨为1%，在A=125处，不能完全分辨，可能会导致产额不准。LEA.51[27]、SEI.51[31]、GRU.51[26]偏离其他数据较大，是因为年代较早，数据陈旧。CHI.87[21]在Z=50的基态累积产额明显偏高，加上Z=50的m态产额，超过了子核的累积产额，物理上不合理，应该为基态与m态之和。经过上述初步分析，对实验数据进行了取舍。结果如图中的YC-FIT和YI-FIT，分别代表拟合的累积产额和独立产额，并与现有数据库的数据进行了比较。B8、JEFF-3.3为美国与欧洲的产额库数据[35-36]。各产额之间的协方差关联系数如图5所示。

x，y坐标0～19对应图4横坐标中470～530的核素的独立产额和累积产额;A=125,En=T图5 nth+235U裂变产额的协协方差关联系数Fig.5 Covariance coefficient of fission yield from nth+235U

横坐标为裂变产物核，用10倍的电荷数(Z)+同核异能态来表示(Isomer=0，1分别为基态和亚稳态)；图例中“-I”结尾的表示独立产额，文献用作者、年代、EXFOR的条目和次条目号来标记，下同图4 A=125的n+235U裂变产额Fig.4 Fission yields of n+235U for A=125

通过对热中子诱发235U裂变质量链A=66～172的独立产额和累积产额实验数据拟合，获得的参数如图6所示。从图6可看出，峰区(A=95、140)的参数与谷区比较涨落较小，谷区A=117部分的误差和涨落比较大，这与实验数据相关，谷区实验数据相对少，且误差较大，峰区的实验数据比较多，且一致性较好。另外，通过该方法，可对产额的合理性作出判断，如图7中Z=55的RUD.90[30]产额，因明显偏离拟合数据的，可认为不合理。图7还示出了A=149裂变产额的统一评价情况，相应的数据列于表3，其中149Nd的独立产额与ENDF/B-Ⅷ.0相差24%。

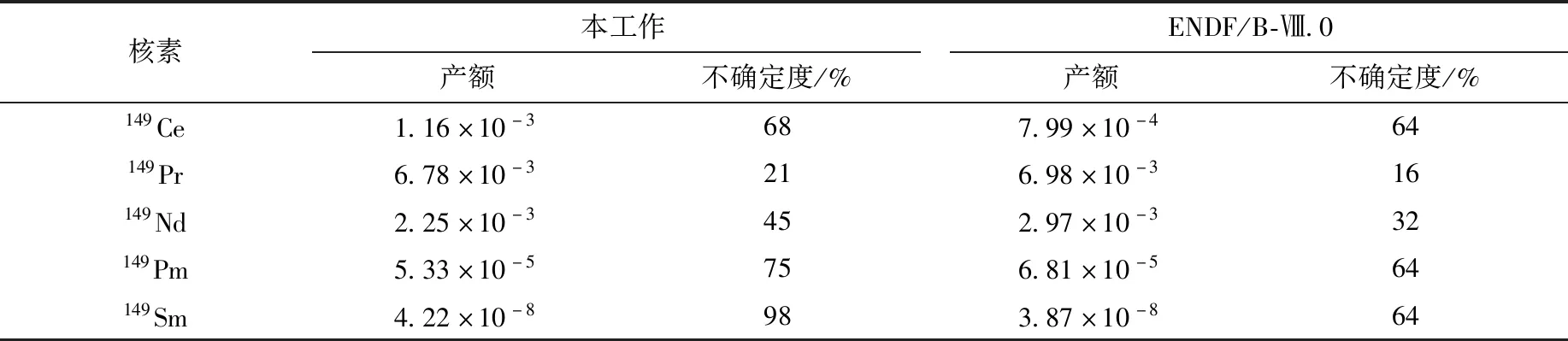
表3 A=149的nth+235U评价裂变独立产额Table 3 A=149 evaluated fission independent yield from nth+235U

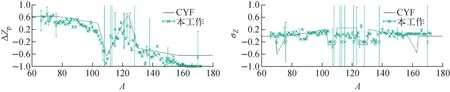
图6 nth+235U裂变Zp模型参数Fig.6 Parameter of Zp model for nth+235U fission

4 不确定度数值结果

基于上述评价方法建立的中子诱发235U裂变产额数据库，采用NECP-SUNDEW计算程序，以UAM[37]燃耗基准题的TMI-1燃料栅元为对象，计算了本文产额数据对栅元特征值、重要核素原子核密度引入的不确定度，并与基于ENDF/B-Ⅷ.0库的结果进行了比较。

4.1 栅元特征值kinf的不确定度

表4列出了7个燃耗深度下，本工作的nth+235U裂变独立产额和ENDF/B-Ⅷ.0的产额数据传递给栅元kinf的相对不确定度。可看出，不同燃耗深度下，两者传递的不确定度始终非常接近。这是独立产额协方差矩阵内含有大量负值，这些负相关性的影响随着燃耗加深、裂变产物增加而逐渐增大，导致最终kinf的不确定度不会明显增大。

表4 nth+235U裂变独立产额传递给栅元kinf的相对不确定度Table 4 Cell kinf relative uncertainty transferred from fission independent yield of nth+235U

4.2 核素原子核密度的不确定度

表5和表6分别列出了60 GW·d/tU的燃耗深度下，独立产额传递给重核、裂变产物原子核密度的相对不确定度。可看出，13种锕系核素的原子核密度不确定度并未因使用不同的裂变产额数据而出现大的变化；对于18种裂变产物核素，大部分核素的原子核密度同样变化不大，但对于149,150,151,152Sm和151Eu几种核素，本工作的产额传递了较大的不确定度。这些核素对反应堆的反应性具有重要的影响，另外对乏燃料的贮存、运输、处理过程也有重要的影响。因此，本文选择了这些核素进行分析。

表5 nth+235U裂变独立产额在60 GW·d/tU传递给重核原子核密度的相对不确定度Table 5 Relative uncertainty of nth+235U fission independent yield transferred to heavy nucleus nuclear density at 60 GW·d/tU

表6 nth+235U裂变独立产额在60 GW·d/tU传递给裂变产物原子核密度的相对不确定度Table 6 Relative uncertainty of nth+235U fission independent yield transferred to fission product nuclear density at 60 GW·d/tU

通过NECP-SUNDEW程序分析，149Nd独立产额对这几种核素的原子核密度不确定度贡献最大，如表7所列。图8为程序使用的燃耗链，显示了不确定度在上述核素间的传递过程。宏观响应量的不确定度取决于核数据的相对灵敏度系数和核数据的协方差矩阵，相对灵敏度系数维持不变，因此与ENDF/B-Ⅷ.0结果的差异来源是产额协方差矩阵。图8中的部分产物，本工作的独立产额及不确定度与ENDF/B-Ⅷ.0存在差异，造成了计算得到的协方差矩阵的差异，进而造成压缩协方差矩阵的差异，导致最终结果出现差异。有关149Nd的独立产额数据见表3。

表7 本工作nth+235U裂变149Nd独立产额及所有裂变产物产额传递的相对不确定度Table 7 Relative uncertainty transferred from independent fission yields of 149Nd vs all product’s from nth+235U fission of this work

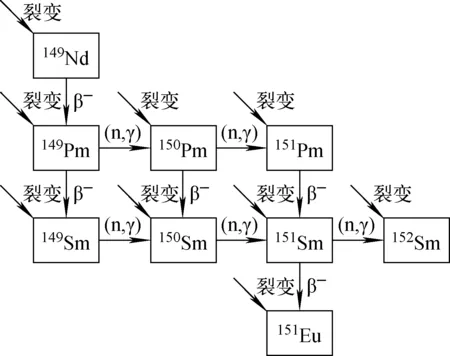
图8 NECP-SUNDEW程序中149Nd及相关核素的燃耗链Fig.8 Burnup chain of 149Nd and related nuclides in NECP-SUNDEW program

5 总结

本文考虑了同一质量链上各产额之间的物理关联，建立了基于Zp唯象模型的裂变产额统一评价方法，可自洽地给出独立产额、累积产额和协方差数据，结果更趋合理。

基于本文评价得到的热中子诱发235U裂变产额及其协方差数据，计算了TMI-1栅元的特征值kinf、重要核素核密度的不确定度，并与基于ENDF/B-Ⅷ.0库的结果进行了比较。结果显示，栅元kinf、重核和大部分裂变产物核素原子核密度的不确定度基本一致。149Sm等几种核素原子核密度的不确定度有所增加，经过分析，主要是因为本工作评价的149Nd等产物核独立产额的不确定度与ENDF/B-Ⅷ.0比较偏大，使得上述几种核密度的不确定度偏大。这样，通过燃耗不确定度分析，可对产额评价起到指导作用。