基于协变密度泛函理论的258Fm诱发裂变动力学研究
陈盛远,李泽宇,陈永静,李志攀,*
(1.西南大学 物理科学与技术学院,重庆 400715;2.中国原子能科学研究院 核数据重点实验室,中国核数据中心,北京 102413)
原子核裂变在能源、国防、工农医等领域中扮演着至关重要的角色,一直是核物理以及工程物理中的重要研究对象。在基础研究方面,裂变是决定超重元素稳定性的主要因素之一[1];决定着星系演化中重元素核合成r-过程的终点以及所合成核素的丰度[2];也是产生短寿命奇特原子核的重要途径。因此,原子核裂变研究是当今核物理的重要前沿课题[3-4]。
重核裂变是低能核物理中最复杂的问题之一[3-5]。由于重核中通常包含着数以百计的核子通过多体相互作用耦合在一起,使用第一性原理计算(abinitiocalculation)或相互作用壳模型(interacting shell-model)研究如此复杂的多体问题尚不太现实。因此,当前对于重核裂变的微观研究通常基于原子核能量密度泛函理论(density functional theory, DFT)。原子核DFT同时考虑了Pauli不相容原理以及核子-核子间相互作用,且自洽地包含了壳效应和量子多体效应,能给出结构更复杂的裂变位垒和断点性质。近年来,基于DFT对重核裂变位能曲面及裂变位垒开展了一系列的研究工作[6-19],深化了人们对裂变机制的微观认知。
然而,为研究裂变动力学性质并定量描述各类观测量,必须在DFT中引入含时动力学演化,即发展时间依赖的密度泛函理论(TDDFT)[20-21]。一般情况下,TDDFT计算只能给出原子核裂变的最可几路径,并不能描述裂变全过程和产物分布。最近,人们基于TDDFT开展了一些尝试以给出裂变产物分布,并取得了卓有成效的进展[22]。
含时生成坐标方法(time-dependent generator coordinate method, TDGCM)将原子核波函数描述为集体形变空间中内禀态的叠加,能自洽包含裂变过程中的量子涨落效应,是一种完全量子化的方法。基于DFT,通过引入绝热近似和高斯重叠近似(Gaussian overlap approximation, GOA)[4-23],构建了可用于实际计算的TDGCM+GOA框架并编写了相应的计算程序[24-28]。在该框架中,含时Hill-Wheeler方程退化为集体空间中局域的含时类薛定谔方程,其动力学性质完全由DFT计算得到的多维位能曲面和质量参数等决定,求解该方程即可得到裂变碎片分布等观测量。该方法最早可追溯到1991年,Berger等提出了时间依赖的集体模型处理原子核裂变,用TDGCM+GOA计算了238U核的裂变碎片动能以及质量分布[24]。随后,基于非相对论Skyrme或Gogny泛函,采用TDGCM+GOA研究了一些锕系核的非对称裂变[25-33]。如Regnier等同时采用Skyrme和Gogny泛函很好地再现了中子诱发239Pu裂变产物分布,并探讨了不同的裂变初态、质量参数等对计算结果的影响[30]。最近,粒子数投影、角动量投影、热涨落等被相继引入TDGCM+GOA框架[33-35],进一步改善了模型对实验结果的定量描述能力并拓展了使用范围。
协变密度泛函理论(covariant DFT, CDFT)在研究原子核结构性质上取得了很大成功[36],其包含诸多优点,如标量、矢量密度相互竞争给出新的饱和机制以及自然给出自旋-轨道耦合势等。近年来,CDFT被广泛应用于原子核裂变的研究中,很好地再现了重核的裂变位垒结构及自发裂变寿命等[10,11,17,37-39]。2017年,基于CDFT构建了TDGCM+GOA并详细研究了226Th光致诱发裂变动力学性质,定性再现了裂变产物分布三峰结构,并探讨了对关联强弱对产物分布的影响[39]。随后,模型被推广至有限温度并系统研究了锕系区原子核的非对称裂变[34]。
本文将采用基于CDFT的TDGCM+GOA详细分析258Fm对称裂变,包括静态位能曲面、剪裂线及其组态的核子密度分布、总动能分布、集体空间波函数演化及裂变碎片质量分布等,并探讨剪裂线的不同判据对总动能及碎片质量分布的影响。
1 基于协变密度泛函的含时生成坐标方法
低能核裂变可近似描述为1个由少量集体自由度决定的缓慢绝热过程,本文将采用TDGCM+GOA模型开展研究。在绝热近似下,原子核的内禀核子自由度与集体形变自由度退耦合,因此计算可分为相对独立的两步。第1步,采用约束的CDFT计算原子核在不同形变下的内禀组态,以得到原子核的位能曲面、集体质量、剪裂线、碎片核子数等;第2步,基于CDFT计算得到的集体参量构建四极-八极形变空间的含时类薛定谔方程,求解即可得到集体波函数的动力学演化及裂变产物分布等。关于模型的详细介绍参见文献[40]。
1.1 约束CDFT求解集体参量
为研究裂变,需对CDFT进行如下约束计算:
(1)
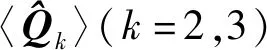
(2)
(3)
式中,R0=r0A1/3,为原子核半径,取r0=1.2。
由约束CDFT出发,自洽求解单核子Dirac方程并结合对关联BCS方程便可得到不同形变(β2,β3)下原子核总能量、单核子波函数及占据几率等,进而可计算原子核微观集体质量Bkl(k,l=2,3表示原子核在四极形变和八极形变方向上的集体惯量)和集体势场Vcoll。通过微扰推转近似[41-42],集体质量可表示为:
(4)
M(n),kl(β2,β3)=
(5)
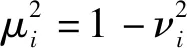
Vcoll(β2,β3)=Etot(β2,β3)-ΔVvib(β2,β3)-
ΔVrot(β2,β3)=Etot(β2,β3)-
(6)
式中,I为转动惯量,由Inglis-Belyaev公式[45-46]计算得到。
1.2 含时类薛定谔方程
以原子核形变参数β2和β3为生成坐标,采用高斯重叠近似,从含时Hill-Wheeler方程出发可推导出集体空间中局域的含时类薛定谔方程:
(7)
式中,g(β2,β3,t)为在(β2,β3)形变空间中的集体波函数,集体参量Bkl和Vcoll皆由CDFT自洽计算得到。求解该方程即可得集体波函数随时间的演化,进而可计算概率流密度:
(8)
为计算碎片分布还需定义剪裂线,即原子核拉伸到刚好要断裂时所对应的形变组态的集合。首先定义脖子处核子数算符:
(9)
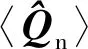
(10)
即可得到该线元对应断裂组态发生的概率,考虑整个剪裂线即得到最终产物分布。
2 结果讨论
本节详细分析258Fm对称裂变的理论计算结果,数值细节如下:CDFT计算采用相对论PC-PK1泛函[47],对关联由BCS方法描述,其中δ-对力的强度参数通过再现由五点公式[48]计算得到的奇偶质量差给出:Vn=351 MeV·fm3,Vp=366 MeV·fm3。形变约束计算的范围为β2∈[-0.96,6.0],β3∈[0.00,3.12],步长为Δβ2=Δβ3=0.04。采用Felix2.0程序[28]模拟核裂变随时间的演化过程,时间步长δt=5×10-4zs。在剪裂线外的区域,考虑集体波包逃逸的附加虚吸收势参数为:吸收率r=30×1022s-1,吸收带宽度w=1.5。
2.1 位能曲面与剪裂线
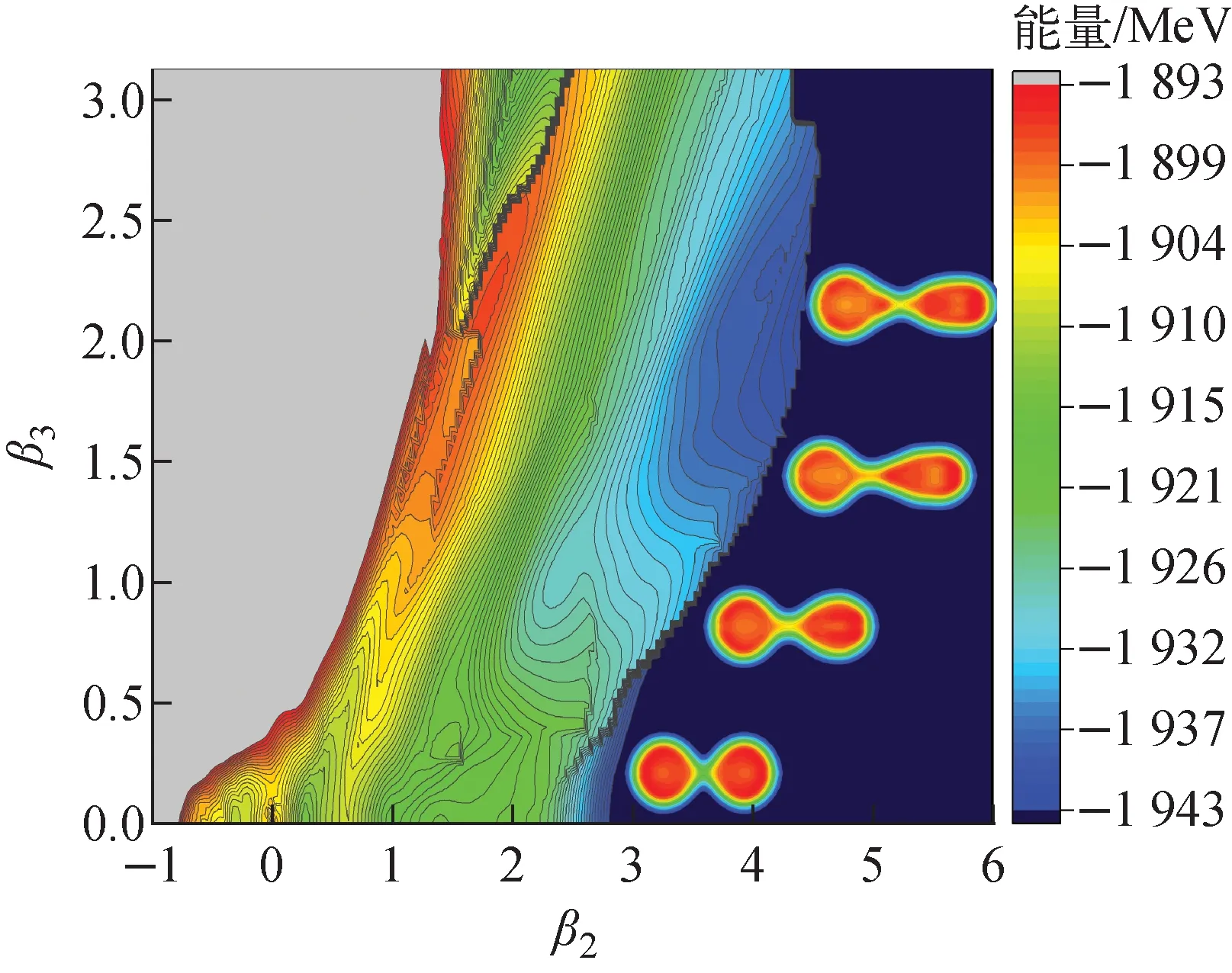
核密度分布图由下至上对应的(β2,β3)分别为(2.36, 0.00)、(3.24, 0.76)、(4.28, 1.60)和(4.36, 2.24)图1 约束CDFT计算得到的258Fm裂变位能曲面在(β2,β3)平面上的分布Fig.1 Potential energy surface of 258Fm in (β2,β3) plane calculated by constrained CDFT
图1给出了CDFT约束计算得到的258Fm裂变位能曲面在(β2,β3)空间的分布,以及部分形变组态(β2,β3)=(2.36,0.00),(3.24,0.76),(4.28,1.60),(4.36,2.24)对应的核子密度分布。在第1个势阱内,能量最低点位于(β2,β3)约(0.28,0.00)附近。在(β2,β3)约(0.68,0.00)处存在裂变位垒,垒高7.3 MeV。在大形变处位能曲面处展现出两个裂变谷,分别为(β2,β3)约(1.50,0.00)至(3.00,0.00)的对称裂变谷,以及(β2,β3)约(2.50,0.50)至(4.40,2.24)的非对称裂变谷。发生对称裂变时,由于对称裂变产物129Sn为幻数核,子核更倾向于近球形而不会具有较大形变。因此,对称裂变谷对应的β2较小,仅约1.5,与Gogny D1S有效相互作用的计算结果一致[49]。
由于大形变组态的复杂性,位能曲面中不同区域的原子核组态的脖子处核子数变化趋势并不一致,导致不同Qn判据给出的剪裂线存在差异,进而影响裂变总动能及碎片分布。图2a给出了Qn=4,3,2,1得到的剪裂线在(β2,β3)平面的分布。在非对称裂变谷附近,Qn=4,3,2的剪裂线明显分开,而Qn=2,1的剪裂线则近乎重合。这是由于在非对称裂变谷末端(图2c),随β2增大,脖子处核子数会平滑减少至2.7左右,再跳变至0.1以下。沿对称裂变谷(图2b),脖子处核子数由3.2跳变为1.6后再相对缓慢降至0.1以下,导致Qn=4,3,2时的剪裂线对应的β2取值接近2.38,而Qn=1时的剪裂线对应的β2取值为2.58。虽然剪裂线的不同对集体波函数的演化影响甚微,但仍可能带来裂变碎片总动能、碎片产物分布的差异。
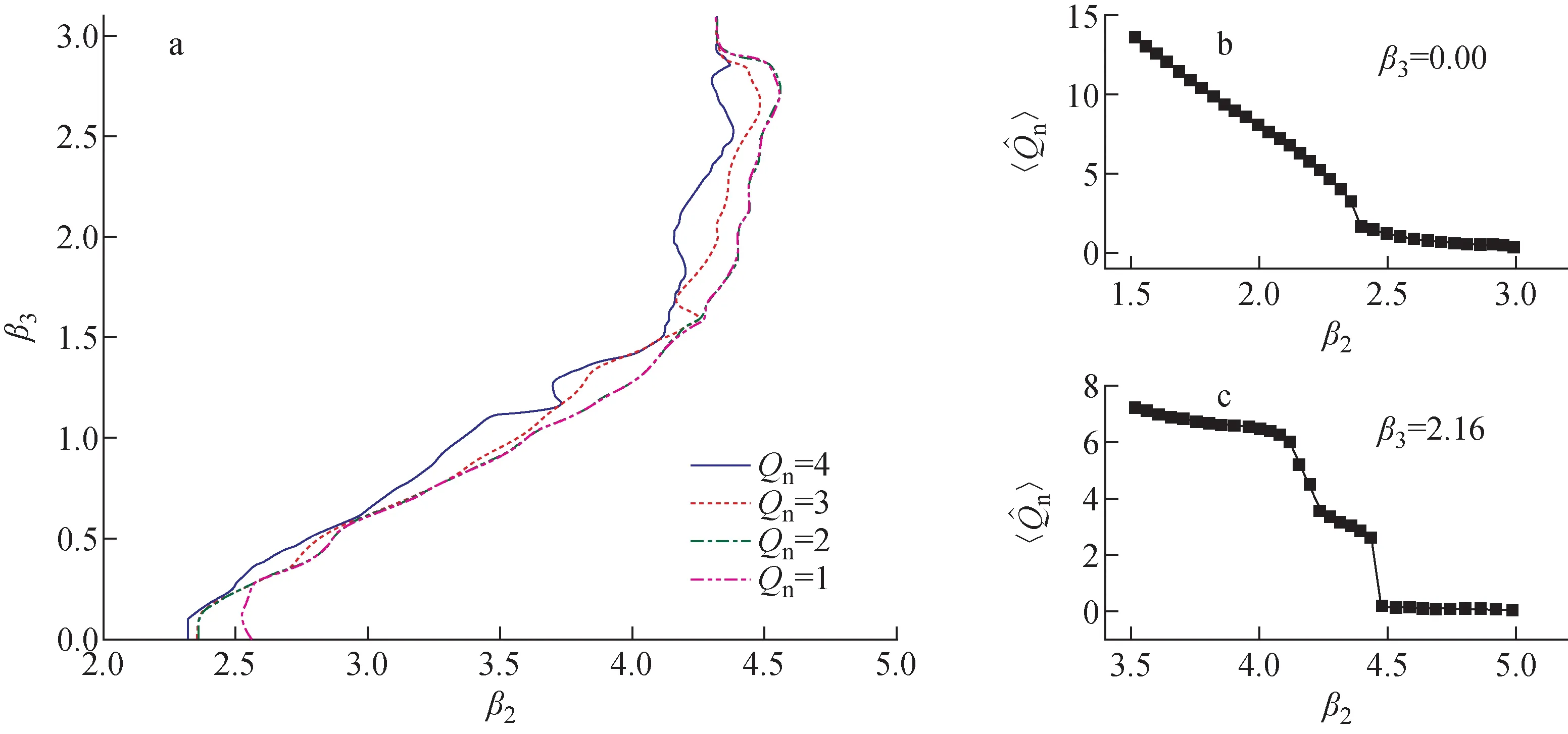
图2 258Fm剪裂线在(β2,β3)平面的分布(a)和β3为0.00(对称裂变谷)(b)以及2.16(非对称裂变谷)(c)时脖子处核子数随β2的变化关系Fig.2 Scission lines for 258Fm in (β2,β3) plane (a) and evolution of number of nucleons in neck as functions of β2 for β3=0.00 (b) and 2.16 (c)
2.2 裂变碎片总动能
根据裂变剪裂线的定义,可采用库伦公式估算裂变碎片总动能(TKE)随核子数的分布:
(11)
式中:e为电荷单位;dch为两碎片电荷中心之间的距离;ZH与ZL分别为重、轻碎片的质子数。
图3展示了不同Qn判据给出的258Fm初级碎片总动能随碎片质量数的分布,作为比较,图中展示了Faust的计算结果(黑色方块)[50],由于目前模型的局限性,暂时无法给出文献[51]中碎片总动能的概率分布。总动能分布呈明显的单峰结构,这是由于对称裂变发生时,两个碎片距离较近,仅14.5 fm(作为比较,同为锕系核的226Th发生对称裂变时,碎片距离为19.86 fm,Qn取3.0)。随着碎片质量数偏离平均分裂,碎片之间的相对距离变长(β2增大,见图2a),总动能降低。不同Qn对应的总动能分布峰值接近。但Qn较大时的TKE分布更离散,这是由于非对称裂变时,越大的Qn取值对应着越小的β2形变以及更近的碎片距离。值得注意的是,碎片质量数122和135附近存在两组明显不同的总动能。其原因是(β2,β3)约(3.24,0.76)以及(β2,β3)约(4.28,1.60)附近区域给出了相似的轻重碎片质量数(密度分布见图1),但断裂时的碎片距离不同。能量密度泛函在计算裂变位能曲面时,由于剪裂线附近组态复杂,存在组态跳变情况,导致沿剪裂线的碎片质量并不连续,因此,计算得到的总动能存在不连续的情况,如图3中给出沿剪裂线重碎片随八极形变变化的插图所示。

图3 不同Qn判据给出的258Fm初级碎片总动能随碎片质量数的分布Fig.3 Total kinetic energy distributions of fission fragment mass of 258Fm for different definitions of scission line
2.3 集体空间中波函数的演化
类薛定谔方程描述了集体波函数在形变空间中的演化规律,它和初始条件(初态)、边界条件一起决定了最终的碎片分布。在本文中,初态的构建方式与文献[39]相同,激发能为8.3 MeV(高于裂变势垒1 MeV)。剪裂线外部区域采用能量线性下降的方式进行外推,即以剪裂点为初始点,β2每增大0.04,能量降低1 MeV。图4给出了不同时刻集体概率密度|g|2在(β2,β3)平面上的分布,红色线条为Qn=3.0时定义的剪裂线。图4a对应波函数演化的初态,其主要分布于第1个势阱内。随着时间推移,波函数开始朝着大形变方向演化(图4b)。由图4c、d可看出,集体波函数主要于(β2,β3)约(2.36,0.00)附近的对称裂变道流出,从微观演化的角度说明了258Fm主要发生对称裂变。小部分集体波函数从(β2,β3)约(4.36,2.24)附近的非对称裂变道流出。需注意的是,(β2,β3)约(1.40,2.00)附近也有极小部分集体波函数流出,这是因为位能曲面中同时包含了结团发射(52Ca)的反应道,但此处流出的波函数通量相比裂变道可忽略。
2.4 裂变碎片分布
在剪裂线上累计集体流的通量,通过高斯平滑[28]后即可得到裂变碎片分布如图5所示,蓝色实线、红色短划线、绿色点划线和紫色双点划线分别对应于剪裂线判据采用Qn=4,3,2,1的产物分布,黑色实心方块为Flynn于1975年测得的热中子诱发裂变的发射中子后碎片分布数据[52],黑色空心圆形和灰色实心方块分别为Hoffman于1980年和Hulet于1989年测得258Fm自发裂变的发射中子后碎片分布数据[51,53]。整体而言,258Fm以对称裂变为主,在A约108、150附近理论计算给出矮峰。随着剪裂线Qn取值由4降至1,对称裂变峰值由9.88%提升至10.28%,非对称裂变峰降低并向外偏移。当Qn取4时,非对称裂变峰在核子数为110以及148处达到峰值,Qn取1.0时则在108以及150处达到峰值,非对称裂变峰位移动2个核子。
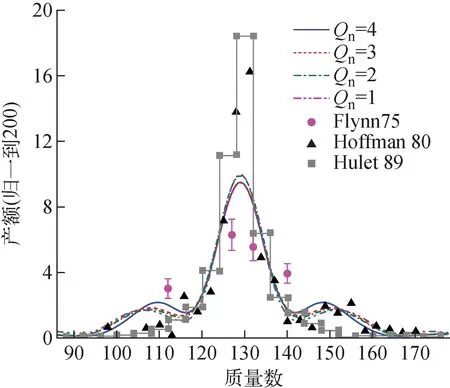
图5 TDGCM+GOA计算得到的258Fm诱发裂变(中子发射前)碎片质量数分布并与实验结果(中子发射后)[51-53]进行比较Fig.5 Preneutron-emission mass yield for induced fission of 258Fm calculated by TDGCM+GOA in comparison with available data (postneutron-emission)[51-53]
值得注意的是,计算给出的碎片分布峰值介于诱发裂变实验数据与自发裂变实验数据之间,该差异可能与初态激发能有关。针对不同激发能计算得到的碎片分布如图6所示(Qn=4)。随着激发能从8.3 MeV增加至17.3 MeV,集体波函数在集体空间中的演化变得更加弥散,导致对称裂变峰值由9.88%降至8.55%。这与实验数据中自发裂变峰值较高,诱发裂变分布更平缓的表现一致。Regnier等基于Gogny D1S参数组也研究了Fm同位素链裂变动力学[32],同样给出了258Fm裂变碎片峰值随激发能升高而降低的演化趋势。与本文相比,文献[32]中的碎片分布峰值更低,改变激发能带来的碎片分布变化更剧烈。

图6 258Fm诱发裂变(中子发射前)碎片质量数分布随激发能的改变并与实验结果(中子发射后)[51-53]进行比较Fig.6 Preneutron-emission mass yields for induced fission of 258Fm with different excitation energy in comparison with available data (postneutron-emission)[51-53]
3 总结与展望
基于协变能量密度泛函PC-PK1计算了258Fm在四极形变与八极形变自由度下的裂变位能曲面,在(β2,β3)约(0.68,0.00)处存在裂变位垒,垒高7.3 MeV,垒外存在路径较短的对称裂变谷和路径较长的非对称裂变谷。由脖子处粒子数Qn定义的剪裂线组态出发计算得到了裂变碎片总动能分布,其呈现明显的单峰结构,且随Qn增大总动能分布变宽。进一步采用TDGCM+GOA方法计算了258Fm低能诱发裂变时集体波函数在四极-八极形变空间中的演化,分析了剪裂线和激发能对裂变碎片质量分布的影响。研究表明,258Fm低能诱发裂变的碎片质量分布同样呈现单峰结构,随着剪裂线Qn取值降低,对称裂变峰值由9.88%增至10.28%,非对称裂变峰降低并偏移。同时碎片质量分布受激发能影响,对称裂变峰随激发能增加而降低,与实验数据给出的趋势一致。
虽然剪裂线带来的影响并不会导致碎片分布结构的实质性改变,但如何减小甚至消除其带来的不确定性,特别是对称峰的高低以及非对称峰位的改变。一个可能的解决方案是在计算中添加对脖子处核子数的约束,实现四极、八极以及脖子处核子数的(β2,β3,Qn)三维约束计算,此外,多维约束的引入有望实现总动能的概率分布。Han的研究表明[54],在已有四极矩与八极矩约束计算中考虑脖子处核子数的约束后,得到的多维集体空间中相邻形变点的密度分布将连续变化。在新的多维约束空间中,或许可找到更合适的剪裂线定义,从而得到稳定且与实验更符合的结果。

