弱外交换超半群

赵云平，谢祥云，李春燕

（五邑大学 数学与计算科学学院，广东 江门 529020）

1 引言与预备知识

1991 年，Lajos[6]引入了外交换半群的概念，称一个半群是外交换的，如果该半群满足一置换恒等式，即对任意x, y ,z ∈ S，有xyz =zyx. 1992 年，M. Yamada[7]给出了外交换半群的构造. 2006 年，Stevanovic 和Protic 引入了弱外交换半群的概念[8]，并于2009 年指出弱外交换半群是a-连接半群的半格分解[2].

1934 年，F. Marty 在第八届Scandinavian 数学家大会上首次提出了超代数系统理论，作为经典代数结构的泛化，在超结构中两个元素的运算是一个集合. 印度数学家M. K. Sen 真正地将半群代数理论和超结构完美结合，他研究了模糊超半群的相关理论[9]. 从1999 年起，各国学者们在超半群的基本理论的基础上，在如超半群上的正则二元关系、超半群的超理想[9]、超半群上的同余[11-15]等方面做了一些基础工作. 本文介绍a-连接超半群、弱外交换超半群和中间超半群的概念，给出了它们的相关性质，并证明弱外交换超半群是a-连接超半群的半格分解，以及中间超半群是a-连接超半群的带分解

2 弱交换超半群

定理1设S 是超半群，，在S 上定义一个新运算“*”满足：对于任意，有x * y=x ° a ° y，则是超半群.

证明对于任意

显然有

推论1超半群S 是交换的，则（ S ,a ）是交换超半群.

因为

基于上述事实，本文引入以下概念

定义6设S 是超半群，，对于任意，使半群.

下面的例子说明弱外交换超半群是存在的.

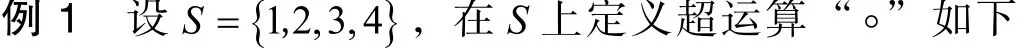
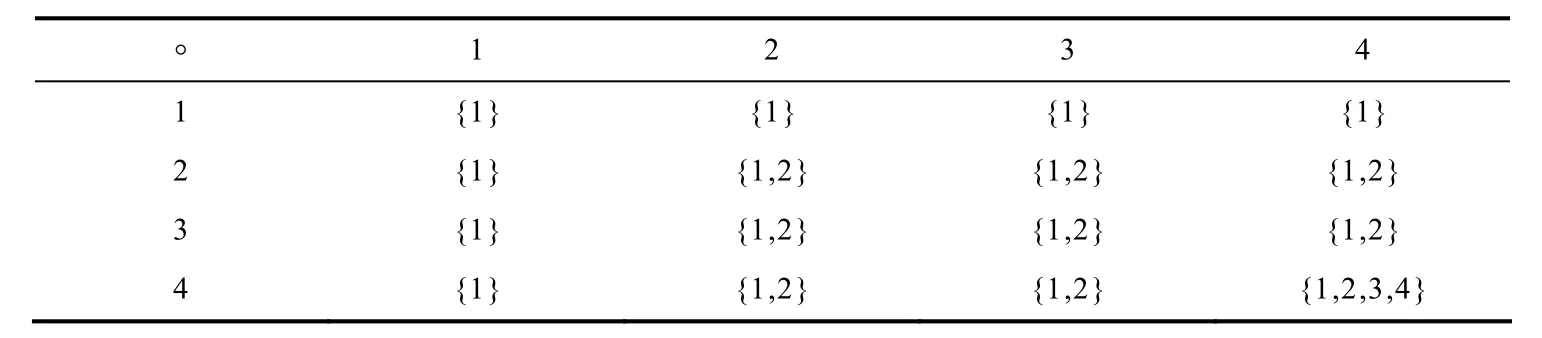
° 1 2 3 4 1 {1} {1} {1} {1}2 {1} {1,2} {1,2} {1,2}3 {1} {1,2} {1,2} {1,2}4 {1} {1,2} {1,2} {1,2,3,4}

情形一：KKK. 根据定义，因为K 是超半群，满足结合律，故在KKK 这种情况满足结合律的.

情形二：

情形三：

情形四：

情形五：

情形六：

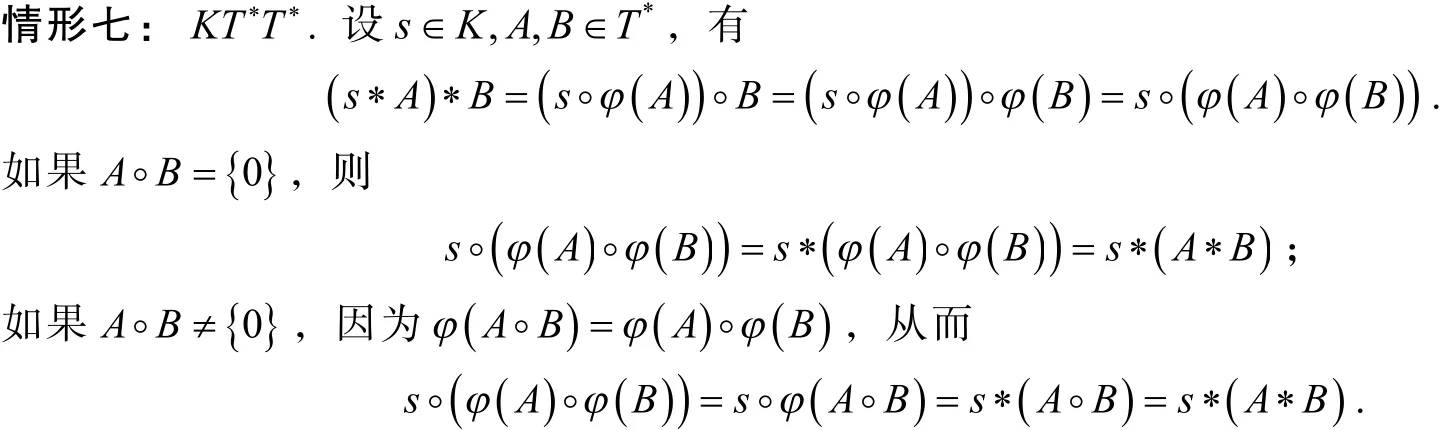
情形八：. 设，我们有以下两种情形：

定理2S 是弱外交换超半群，，则S 是连接的超半群的半格分解.

证明在S 上定义一个关系ρ 如下：

根据注2，

因此，

从而

推论1设S 是外交换超半群，对任意则S 是a-连接的超半群的半格分解.

证明设S 是外交换超半群，则S 是弱外交换超半群，且由定理2，得证.

° 1 2 3 1 {2} {2} {2}2 {2} {2} {2}3 {2,3} {2,3} {2,3}

定理3中间超半群是a-连接的超半群的带分解，

证明对，类似定理2 的证明，在( S , ° )上定义一个等价关系 ρa如下：

令z S∈ ，根据中间超半群的定义，则有

进一步地，令x S∈ ，则有

因此，ρa是带同余关系. 且由ρa的定义，知ρa-类是a-连接的超半群，得证.

定义8设S 是超半群，，对于任意，有则 x，y 称为弱a-连接的. 如果对于任意都是弱a-连接的，则称S 是弱a-连接的.

例4设是超半群，若S 是超群，则a °S = S °a =S. 因此对于任意，对于任

例5设，在S 上定义超运算“ °”如下：

° 1 2 3 1 {1} {1} {1,3}2 {1} {1} {1,3}3 {1} {1} {1,3}

容易验证( S , ° )超半群且S 是弱1-连接的，事实上，对于任意，都有. S 也是弱2-连接和弱3-连接的.

我们通过例1 知道， S 不是弱2-连接的.

注3通过上面定理2 及其证明可以看出，如果S 是任意一个超半群，，在S 上定义一个关系ρ 如下：

很容易看出ρ 是S 上左超同余，如果S 是交换的超半群，那么在S 上定义一个超半格同余关系ρ ，且每个同余类是弱a-连接的，则可知S 是弱a-连接超半群的半格.