基于稀疏网格模型和NSGA-II 算法的中型游艇结构轻量化研究

申炜鑫，王汉友，冷学华，刘自浩

（1.五邑大学 艺术设计学院，广东 江门 529000；2.江门市海星游艇制造有限公司，广东 江门 529000）

船舶轻量化是业内研究热点. 在船舶载重量需求已经确定的情况下，减轻空船重量是减轻船舶总体重量、降低船舶建造成本、降低油耗的重要手段之一. 船体结构非常复杂，单一的结构设计已经很难满足现在船舶的高效设计的需求. 在满足结构所需的强度、刚度、以及船体安全性的前提下，实现船舶轻量化，可以为企业节省材料成本，同时提升操作稳定性[1]. 在进行实际结构优化设计时，为减少设计周期，节省复杂仿真计算的时间，代理模型开始得到应用和发展. 而稀疏网格模型[2]需要的样本点数少，且能有效处理高维问题，拟合精度高. 目前稀疏网格模型已在很多领域有应用，但在船体轻量化的应用还比较少. 本文将稀疏网格模型引入船体结构优化设计中，同时结合NSGA-II 算法进行求解，以期在保证求解精度的前提下，完成船舶轻量化，减少计算的时间成本.

1 研究方法

1.1 稀疏网格

稀疏网格理论最早由Smolyak 提出[3]，它是基于不同网格上的解的组合，稀疏网格逼近是适当选择分量的子空间的张量积中解的线性组合函数空间. 通过稀疏网格配点法进行初始样本点选取，用函数积分或者差值逼近的数值方法，将所求解的目标函数近似为一组多维分层基函数的线性组合，通过Smlolyak 规则，以各维度不同水平基函数的张量积为基础，建立起高维问题的求解模型.

在进行稀疏网格插值[4]时，稀疏网格利用自适应局部细化过程，选择响应面中要进一步细化的区域（对稀疏网格模型影响较大或某维度方向难以插值的区域）. 然后对这些区域集中细化，允许响应面以更少的设计点更快达到指定精度水平，非常适用于试验点数较少的高维问题求解. 此外，由于稀疏网格是一种基于网格层次结构的自适应算法，网格插值构造过程中，不需要特定的设计试验. 稀疏网格插值只需要预定义并通过有效控制方式，自动控制样本点的生成.

由于船体结构复杂，所选择的优化参数与约束以及优化目标之间，并没有确定的函数关系，所以本文利用稀疏网格模型来建立其函数关系从而进行优化计算.

1.2 NSGA-II 算法

多目标遗传算法是用来分析和解决多目标优化问题的一种进化算法，其核心就是协调各个目标函数之间的关系，找出使各个目标函数都尽可能达到比较大的（或者比较小的）函数值的最优解集.在众多目标优化的遗传算法中，NSGA-II 算法[5]（Non-dominated Sorting Genetic Algorithms）是影响最大和应用范围最广的一种多目标遗传算法. NSGA-II 算法改进了传统NSGA 算法的缺点，求解速度快，收敛性好. 本文利用稀疏网格模型生成优化所需要的函数关系，并利用NSGA-II 算法进行优化求解，输出最优解集.

2 算例结构分析与优化参数选取

2.1 船体结构有限元分析

本文选择某中型单体游艇作为优化对象，该船舶主要尺寸参数为：船体总长23.28 m，船宽5.8 m，航速22 kn，设计水线长21.26 m. 对于该类型的船舶，其轻量化的意义主要在于节省材料，提高操纵性，降低污染. 在满足结构强度要求下，将各结构厚度作为优化变量，以总质量最小作为优化目标，进行优化计算.

为保证船体的强度要求，根据CCS 规范进行船体结构尺寸设计，并对其强度校核，其中最大剪应力应小于103 MPa，最大等效应力应小于183 MPa. 在进行有限元分析时，需对静水中整船结构进行受载计算. 在计算时，考虑载荷在结构上的实际分布情况下，计算船体的总纵弯矩[6]：

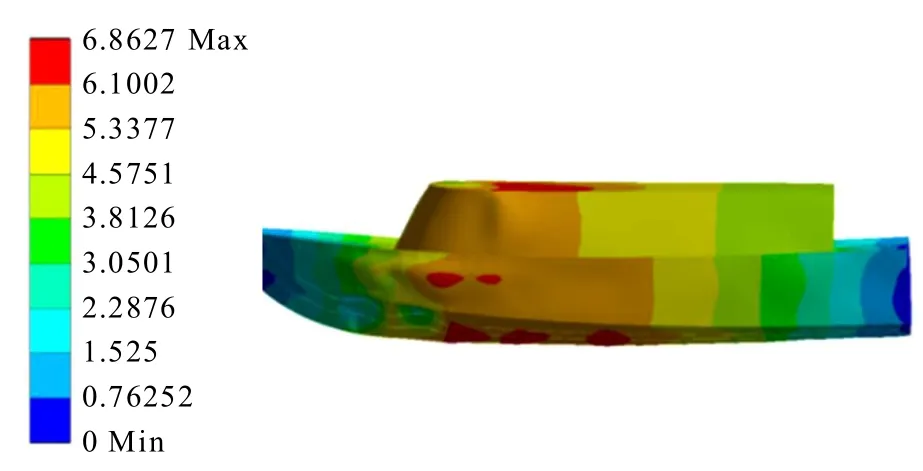
图1 船体结构位移云图

2.2 结构优化参数选取

船体结构复杂，在进行多目标优化时，优化变量过多会增加计算成本. 因此在进行结构优化前先对优化参数进行筛选，结合有限元计算结果，对船体质量和强度影响较大的结构参数进行灵敏度分析. 最终确定了本次所要优化的结构分别是：船底板、水密舱壁板、甲板、上层建筑壁板、2080 平台甲板、肋板等，以结构厚度为变量，分别以来代表这 6 个优化参数，见图2. 表 1 为各结构对应的初始参数值. 选取的优化参数为之后的稀疏网格模型的建立做准备.

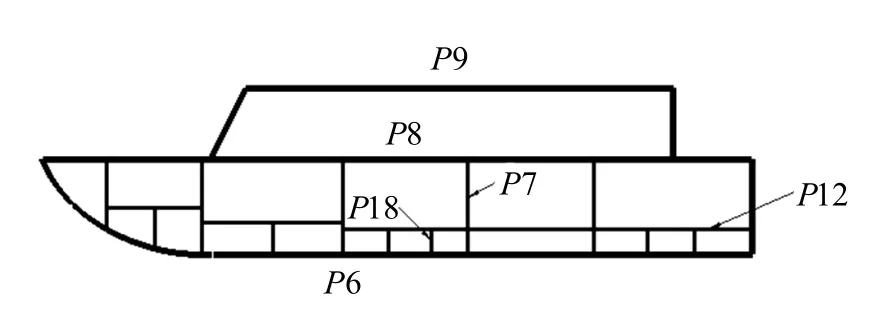
图2 船体结构简图

表1 船体结构初始参数表

3 稀疏网格模型建立与优化

3.1 建立稀疏网格模型

目前应用较广的试验设计有：正交试验、全因子试验、拉丁超立方试验和Box-Behnken 设计等[7].本次使用与稀疏网格模型相适应的试验方法—稀疏网格配点法，通过ANSYS Workbench 中的Design Xplorer 模块进行稀疏网格初始化，自动生成对应的稀疏网格样本点. 稀疏网格初始化生成的样本点多少与所选择的初始参数数目有关. 利用ANSYS 软件进行稀疏网格模型的建立和优化计算，根据生成的样本点进行初始样本点的计算，共生成13 个试验初始样本点.

根据初始样本点生成稀疏网格模型时，考虑试验计算成本和试验次数等因素，结合前人研究经验[4]将输出参数所允许的最大相对误差设定为5%，给定方向细化深度取值为5，将允许生成的最大细化点数设定为1 000. 通过生成的初始样本点和上述参数设定，开始计算. 经过不断的网格细化，如果没有达到预期的精度，算法通过在相应方向上建立新的等级来进一步细化网格. 重复这个过程，当系统计算的误差小于最大相对误差设定值，结束细化过程.

图3 收敛曲线

由于稀疏网格模型是由线性插值得到的点，所以试验样本点在拟合度散点图中均在斜率为1 的直线上. 其拟合精度需要随机验证点进行验证. 图 4 为预测值—观测值散点图，可以看到用于验证的5 个随机点，均能分布在斜率为1 的直线周围或直线上，其结果在设定的误差范围内，可以进行下一步的优化计算.

图4 预测值-观测值散点图

图5 响应面图

3.2 优化计算

在生成的稀疏网格模型的基础上，将总质量最小作为目标函数，将等效应力最大值和剪应力最大值作为约束条件如下式（2），等效应力最大值为，剪应力最大值为. 在结构其他尺寸不变的条件下只对各部件厚度进行优化，考虑到各部件密度一致，所对应的总质量与各结构板厚为线性关系，可直接对部件厚度进行优化，优化目标为总质量最轻，可简化为：，优化变量最小值是根据CCS 规范计算后取圆整化值得到的，由于本次的优化目的是质量最轻，所以参数最大值的选取比优化前的取值略大即可满足优化要求，优化变量取值范围如表2.

表2 优化变量取值

根据上述约束条件、优化变量和目标函数的设定，利用NSGA-II 算法对稀疏网格模型进行优化求解. 考虑到试验相关计算成本和实际多次试验分析验证，设定优化所需初始样本数为 100，每次迭代的样本数为100，收敛稳定性比率为3%，最大迭代次数设定值取20，最大允许Pareto 百分比取70%. 算法收敛需满足以下收敛准则：

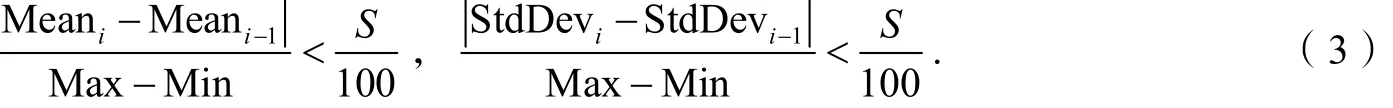
图6 为收敛标准图，图中可以看出在第6 次迭代时收敛稳定性比率达到设定值，同时Pareto 百分比也趋近于设定值，完成优化过程，表明本次优化效果较好. 图7 为优化得到的Pareto 解散点图，最后在此解集中选取3 个候选点.

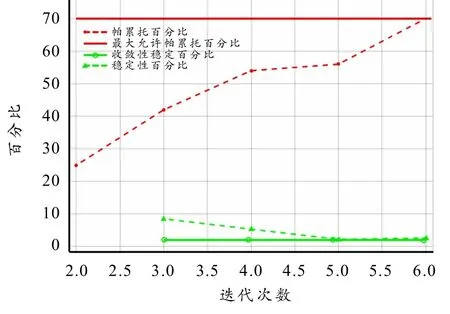
图6 收敛标准图

图7 Pareto 解散点图

解集处理后，优化最终生成3 个候选点，对每个候选点圆整化后，取值的方案如下表3.

表3 优化结果

3.3 优化结果分析

对船体结构进行优化后，各个结构参数均大于最小设计板厚，即满足设计需要. 对结果圆整化之后重新进行有限元计算，方案一质量适中，方案二质量最大，方案三质量最小. 本次优化以质量最小为优化目的，选取方案三作为优化结果进行有限元计算验证，其结果见表4.

表4 优化前后对比

优化后船体总质量为13 468 kg，与优化前对比，整船质量减少了 15.6%，最大等效应力为159.11 MPa，最大剪应力为65.70 MPa，均符合整体强度要求. 通过该优化方法能够在满足船体强度的同时有效减小船体总质量，实现船体轻量化.

4 结论

本文针对船舶结构复杂、优化变量多等问题，利用 ANSYS 有限元分析软件，利用稀疏网格模型与NSGA-II 算法结合的方法进行船舶结构优化求解. 在保证船体结构强度的前提下，优化后的整船质量减少了 15.6%. 验证了该方法的有效性，也为相关工程领域的类似问题提供了新思路、新想法. 由于船舶结构复杂，本次只考虑船在静水情况下进行优化分析，下一步将结合船在波浪中的受载情况，对船体结构进行进一步优化，使优化结果更加符合实际要求.