基于小初衔接『角有关知识』的拓展性探究活动的设计与思考

文 蓝海鹏

小学阶段，学生在相关年级已经学习了角的有关知识。在六年级复习时，需要把这些零散的知识整合起来，通过小专题的复习，促使学生将知识结构化，提升学生的综合运用能力。同时，通过整合和拓展，有效加强小学数学与初中数学的衔接。如何基于学生对角有关知识的认识设计小初衔接拓展课呢？从中又有哪些思考？笔者设计了以下五个关于角的认识的探究性活动并加以实践，取得了较好的效果。

一、如何用火柴判断两角是否相等

（一）设计说明。

此探索活动，综合了“角的认识”“图形的运动”等知识。指向发现三角形全等判定（三边对应相等，两三角形全等）和全等三角形的性质（两三角形全等，对应角相等）。

（二）活动设计与教学实施。

1.提出问题。

你能用火柴棒判断两个角是否相等吗？

准备：一把三角尺、两根长度相等的火柴棒。

呈现《学习单》：

2.尝试解决。

学生在《学习单》上摆动火柴棒进行自主探究，再小组交流。

3.全班交流。

小组代表上台汇报，教师梳理、引导。

（1）正向探索。呈现学生作品图1 和图2，你看得懂吗？

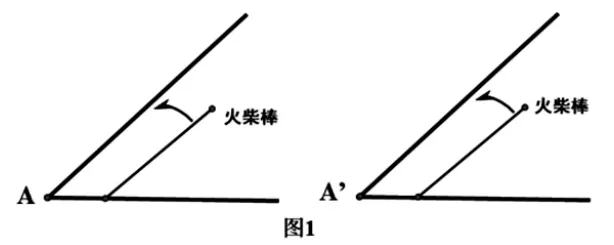
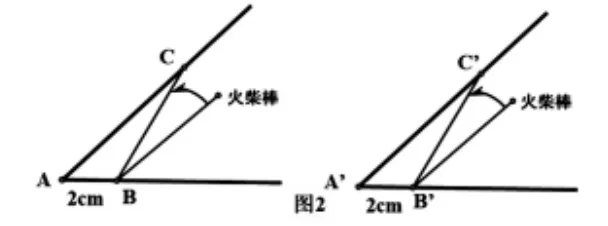
解读：分别在∠A 和∠A′的水平方向的边上找点B 和B′，使AB=A′B′=2cm。火柴的一端放在点B 和B′上，另一端“斜靠”在角的另一边上。问：图中有哪些等量？怎样验证你的猜想？学生采用度量等方法进行验证。交流发现：如果AC=A′C′，那么可以判断∠A=∠A′。

进一步提出猜想：点B 和B′水平移动，如图3，如果AB=A′B′=3cm，测得AC=A′C′，可以判断∠A=∠A′吗？

得出结论：如果AB=A′B′（或等于2cm、3cm……），火柴棒BC=B′C′，只要AC=A′C′，就可以判断∠A=∠A′。

（2）逆向探索。进一步猜想：画出两个不相等的角，如图4，∠A≠∠A′，AB=A′B′=3cm，观察得到AC≠A′C′。

得出结论：如果∠A≠∠A′，那么AC≠A′C′。

4.归纳总结。

从刚才的探索中你发现什么？

（1）概述探究过程与结论。解决这个问题的思路为：把火柴棒“卡”在角的内部，火柴棒的一端分别放在两个角水平边上的同一个位置（即AB=A′B′），如果火柴棒靠在另一边的位置也一样（AC=A′C′），那么∠A=∠A′。如果火柴棒靠在另一边的位置不一样（AC≠A′C′），那么∠A≠∠A′。

（2）发现新知识。两个三角形三条边对应相等时，这两个三角形形状、大小一样，（如果把它们剪下来重叠，它们会完全重合），这时∠A=∠A′。

二、如何在方格上画出与已知角相等的角

（一）设计说明。

此探索活动，综合了“角的认识”“平行线的认识”等知识。指向发现平行线的性质（两直线平行，同位角相等）和角的倾斜程度。

（二）活动设计与教学实施。

1.提出问题。

如图5，已知方格图上有∠AOB，你能画出若干个与∠AOB 相等或不相等的角吗？画好后对比分析，思考：与已知角相等的角有什么关系？与已知角不相等的角有什么特点？

2.学生独立操作，再交流自己的发现。

3.交流反馈。

呈现图6 和图7，仔细观察，你发现了什么？

学生发现：图6 和图7 中，这些相等的角的一边都在同一直线上，另一条边都经过一个“田字形”的左下角和右上角的顶点（在“田字形”的一条对角线上）或者是互相平行的。而图8 中，三个角的一边在同一直线上，已知角的另一边经过一个“田字形”的对角线，所画的两个角的另一边分别在“日字形”和“平放的日字形”的一条对角线上，且三条边是不平行的。

从图7 发现：当∠AOB=∠A1O1B1=∠A2O2B2时，OA、O1A1、O2A2平行。反过来，OA、O1A1、O2A2平行，∠AOB=∠A1O1B1=∠A2O2B2，这三个角的位置是相同的。

对比图6 和图8 发现：当两个角相等时，“倾斜”程度一样；两个角不相等时，“倾斜”程度不一样。“倾斜”程度越大，则角越大。

三、如何借助图形的缩放画出两个相等的角

（一）设计说明。

此探索活动，综合了“角的认识”和“图形的缩放”等知识。指向发现三角形中位线定理（三角形的中位线平行于第三边且等于第三边的一半）和图形的缩放性质。

（二）活动设计与教学实施。

1.提出任务。

请用一把三角尺，请在图9中画出与∠BAC 相等的角。

2.学生探索，独立画图，再小组交流。

3.交流反馈。

观察图10和图11，说一说有什么发现。

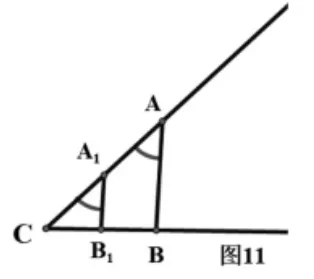
方法1：向外画。如图10，用三角尺在角的两边分别画BB1=CB，AA1=CA，再连接A1B1即得到∠B1A1C=∠BAC。

方法2：向里画。如图11，用三角尺在角的两边分别找到BC和AC 的中点B1、A1，连接A1B1即得到∠B1A1C=∠BAC。

思考：还有其他画法吗？

四、如何借助一个三角尺或三角尺纸片画出两个相等的角

（一）设计说明。

此探究活动，涉及“等角”“画角”“垂直”等知识。通过角的“局部搬迁”实现“整体搬迁”，指向发现全等三角形的判定（SSS）和性质（全等三角形对应角相等）。

（二）活动设计与教学实施。

1.提出任务。

已知∠A，你能用一个三角尺或三角尺纸片画出一个与∠A 相等的角吗？

2.学生尝试画图，画好后交流。

3.集体交流。

呈现学生作品，如图13 和图14。

总结画图步骤：（1）如图13，三角尺或三角尺纸片的直角顶点与∠A 的顶点重合，一条直角边与∠A 水平方向的边重合，∠A 的另一条边与直角三角尺的最长边交于点B，在尺上或三角尺纸片上标注好。（2）如图14，画一条射线A1P，把留在直角三角板最长边的点画出来。经过点A1、B1画射线A1B1，得到∠PA1B1，此时∠PA1B1=∠A。

4.拓展延伸。

（1）这个三角尺或三角尺纸片还可以怎么放？

（2）用另外一个三角尺怎么画？

（3）假设∠A 是一个钝角，怎么画？交流后得到：把钝角分为两部分：直角和锐角。先画一个直角，再用上面的方法画出锐角部分即可（图略）。

五、如何借助尺规画出两个相等的圆心角

（一）设计说明。

此探究活动，综合了“角的认识”和“圆的认识”等内容。指向发现：在同圆或等圆中要画出两个相等的“圆心角”，只需要找到相等的两段弧。与初中的尺规作图、圆心角定理等知识和方法衔接。

（二）活动设计与教学实施。

1.提出问题。

如何利用圆心角画一个与已知角相等的角？

准备：一个圆形纸片，一把没有刻度的直尺、一个圆规。

（1）以圆心为顶点，任意画一个角，得到一个圆心角，如图15。

（2）画一个与这个圆心角相等的圆心角，怎么画？

2.实验路径。

学生选择其中一条实验路径进行独立探索。探索完成后再交流。

实验路径1：第1 组，不给提示，自主探索。

实验路径2：第2 组，（实验单）如图15。你能在圆A 上画一个等于∠BAC 的圆心角吗？

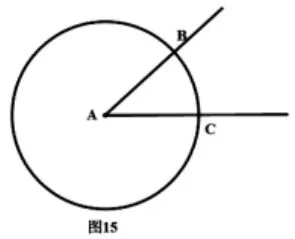
学生探索后交流步骤：（1）剪下这个角，得到一个扇形；（2）在圆上剪一个一样的扇形：把这个角的顶点贴着圆心，弧贴在圆弧上，照着这个扇形的模样剪下来；（3）观察两个扇形，你发现什么相等的量？

学生发现：在同一个圆中，两个相等的圆心角所对的弧是相等的。反过来，要画两个相等的圆心角，只要画出两段相等的弧，再把弧两端的点分别与圆心连接，得到的两个圆心角是相等的。

实验路径3：第3 组，已知∠A=∠B，分别以点A、B 为圆心，以一定长（如3cm）为半径画圆,如图16。你发现什么相等的量？你是怎么发现的？（把两个角剪下来并将它们重叠在一起，或用圆规“测量”两段弧）

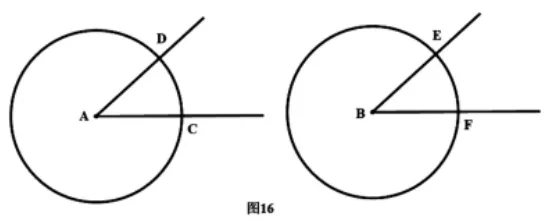
学生发现：两个角“夹”着的弧相等。

3.总结画图方法。

在同圆或等圆中，画一条与已知角所夹的弧相等的弧，把所画的弧的两个端点分别与圆心连接，得到的角与已知角相等。

4.出示题目：已知∠O，画一个∠α，使得∠α=∠O。学生画图。

操作步骤：

（1）以已知∠O 的顶点O 为圆心，以任意长为半径，画一个圆，圆O 交∠O 两边于点A、B。

（2）画射线OC，交圆O 于点C。

（3）在圆O 上截一段弧CD，使得弧CD 等于弧AB。

（4）画射线OD。

此时∠COD = ∠AOB，在∠COD 上标上角的弧线，标注α。

发现：用圆规在同一个圆上，作两段相等的弧，这两段弧所对的圆心角相等

注意事项：教学时，可结合图给出“圆心角”的概念，操作步骤可让学生用自己的语言表达。

上面把小学学过的有关角的认识及相关知识融合起来，形成五个拓展性探究活动，不仅系统地关联角的知识，还通过小专题复习和探究方式获得新知的初步认识，有效发展学生运用所学知识解决问题、探究数学知识的能力。