一类四 估计

靳曼莉

(北华大学数学与统计学院，吉林 吉林 132013)

0 引 言

本文讨论如下四阶抛物型方程初边值问题弱解爆破时间的上界：

(1)

四阶抛物型偏微分方程在材料科学、工程学、生物数学、图像分析中有着诸多的应用，许多作者对四阶抛物型偏微分方程解的存在唯一性、正则性、爆破性等进行了深入研究[1-6].文献[5]深入讨论了如下问题：

(2)

文献[6]研究带有对数非线性项的一类伪抛物方程的初边值问题

证明了该问题的弱解将在有限时间爆破.

文献[7]利用位势阱方法得到问题(1)全局弱解的存在唯一性以及弱解在有限时间爆破.本文将在文献[7]的基础上利用一种新方法得到问题(1)弱解的爆破时间的上界.

1 预备知识

为方便起见，本文中引入以下记号：

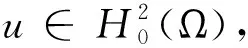
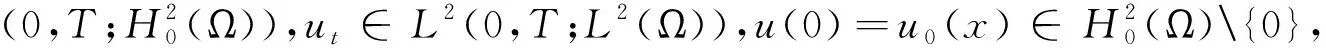
在[0，T]上几乎处处成立.

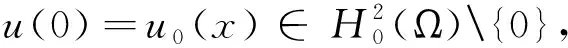
引理2[8]设正的二阶可微函数θ(t)满足不等式

θ″(t)θ(t)-(1+β)θ′2(t)≥0，t>0，

2 主要结果

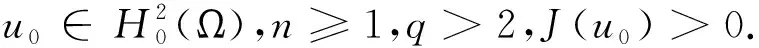
则u(x，t)在有限时间t*爆破，且

证明：问题(1)中第1个方程两端乘u然后在Ω上积分有

即

(3)

下面我们分两种情况讨论.

(ⅰ)对任意t>0有J(u)≥0.

(4)

由Young不等式[9]有

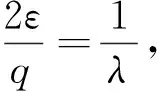
(5)

将式(5)代入式(4)可得

故

(6)

把不等式(6)的右端记为M，则有

从而

(7)

令

则

取充分小的ε使得

(8)

取充分大的常数C使得

(9)

令

则

[φ′(t)]2=(4φ-δ)[y′(t)]2，

从而

4φ(t)[y′(t)]2=[φ′(t)]2+δ[y′(t)]2

.

(10)

即

(11)

由式(11)、Holder不等式以及Young不等式有

(12)

由式(10)知

(13)

利用式(13)、 (10)、 (7)、 (12)可得

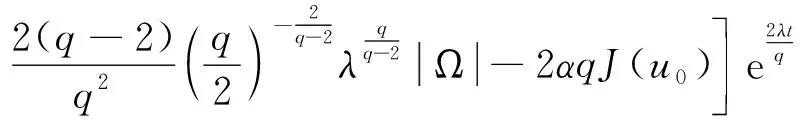
设

由F′(λ)=0可得

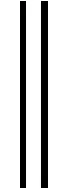
注意到式(8)，我们有

从而

综上

且u(x，t)在有限时间t*爆破.

(ⅱ)存在某个t0>0使得J(u(t0))<0.

令v=v(x，t)=u(x，t+t0).由于J(u)是不增的，所以

J(v(t))≤J(v(0))=J(u(t0))<0.

由式(3)得

(14)

从而

故

(15)

把式(15)代入式(14)得

(16)

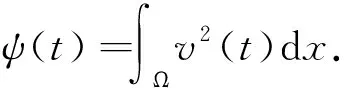
从而ψ(t)-ψ(0)>-2qJ(v(0))t，即ψ(t)>ψ(0)-2qJ(v(0))t，于是对任意t>0有ψ(t)>0.

另一方面，由式(16)有

故

(17)

即

于是由式(17)知，存在