做好错题整理，再生学习资源

侯兴颖

【摘  要】在小学数学学习的过程中，学生会由于本身知识的缺乏、思维能力的滞后、学习习惯的不完善等出现一系列的错误，而学生只会认为是自己粗心大意造成的。学生可以使用错题本将这些错误资源分类整理下来，加强不同错题的理解后可以避免以后出现类似的错误。在“双减”政策的背景下，错题本的使用也可以有效地减少过多的练习，从而减轻学生不必要的作业负担。

【关键词】“双减”政策;小学数学;错题本

所谓“双减”，就是指有效减轻义务教育阶段学生过重的作业负担和校外培训负担，为了有效地推行这项政策，各校都对学生的课后作业进行了一定的整改。同样，为了有效地实施这一政策，笔者所在学校也尝试减少了一部分的数学练习，并系统地形成了课后作业安排。在减负推行的这段时间，部分学生出现了对学习过的部分内容一知半解，甚至对很多知识产生混淆，为了改变这一现状，笔者开始尝试进行错题本的使用和改革。

一、错题本的内涵

（一）错题本的定义

所谓错题本，是指学生在学习过程中，把自己所完成练习中的错题按不同的类别分类整理，便于找出自己学习中的薄弱环节，通过自己分析让理解更深刻，复习更具有针对性，从而提高学习效率的记录本。其实错题本的作用就是学生在学习过程中通过问题的集中处理，抓住学习中的薄弱环节，明确学习的方向，从而提高学习效率。尤其是在目前“双减”的要求下，学生很难从适当减少的练习中及时发现并解决自己的问题，相信错题本的使用可以让他们更好地明确方向，举一反三，高效地解决自己易错的问题。

（二）错题本的使用对象

在何如涛老师的文章中提到，错题是教师和学生在教学和学习过程中的产物，是一种财富，高效地利用数学错题资源，可以促进教师高效地教，学生有效地学。由此可见，错题本不仅是学生的必需品，也是教师的必需品。在教学过程中，学生需要整理自己的错题来发现自己学习上的问题，从而明确自己的薄弱环节，进行针对性的学习;教师也要有错题本，发现自己所教学班级的共性错误，反思是否在教学过程有所疏漏，从而对自己的教学进行查漏补缺，进一步完善自己的教学计划。

（三）错题本的形式

如今，错题本在市面上有各种各样的版本，形式也是各种各样的。在我看来，学生整理错题只需要六大要素：题目，错误的答案，错误的原因，正确的结论，正确的分析，自己尝试举例。一般的错题本对正确的结论比较重视，而忽视了学生对问题的再思考，忽视了学生学习的深入性和生长性，所以我认为错误的原因和正确的分析是尤为重要的。学生独立分析思考，通过自己的方法避免下次犯同样的错误，对于学生来说更具有针对性，也更能培养学生自我完善的意识和掌握自我完善的方法。

錯题整理案例参考

题目：平行四边形相邻的两条边长10厘米和6厘米，一条高是8厘米，这个平行四边形的面积是

（    ）平方厘米。

错误的答案：（80）

错题原因：我没有确定8厘米所对应的底是哪条边长，我把10厘米当作了底，所以用10×8=80平方厘米。

正确的答案：（48）

正确分析：已知平行四边形底（10厘米或6厘米）和高（8厘米），有两种可能性：底10厘米，高8厘米或者底6厘米，高8厘米。假设底10厘米、高8厘米的话，斜边就会是6厘米，出现斜边比高长的现象，不符合三角形的特征;如果底是6厘米，高8厘米，斜边是10厘米，符合三角形的特征，所以用6×8，答案应该是48平方厘米。

举例：平行四边形相邻的两条边长15厘米和9厘米，其中一条高12厘米，这个平行四边形的面积是（108）平方厘米。高12厘米对应的底应该是9厘米，所以用12×9=108（平方厘米）。

二、错题本使用策略

（一）及时整理并正确归因

错题的整理一定要及时，只有新鲜出炉的错题才会让人印象深刻，才能更清晰地知道自己的错误在哪里，从而能够正确归因。在学生初次整理错题时，教师一定要帮助学生学会正确地将这些错误进行分类。在很多学生的观念中，只要出现了错误就认为是自己粗心，归结于心理原因，导致在复习的过程中对此类错题不够重视，失去了错题本真正的意义。为了进一步改变这样的情况，教师不仅要在第一次帮助学生正确归因，更要在平时面批的时候多问问学生错误的原因，同时，可以让学生对不同类型的错题采取不同形式的标记，这样在今后的回顾、完善时，会更具有针对性。当然也可以用红笔写错误答案和原因，用蓝笔写正确答案和解析，最后用黑笔再次举例验证，整个过程清晰明了，长期这样坚持，我想学生会有很好的收获。

（二）及时回顾并正确总结

对于学生错题的分类，国内外的意见各不相同，我比较认同叶静老师分的四大类：知识性错误、逻辑性错误、策略性错误、心理性错误。

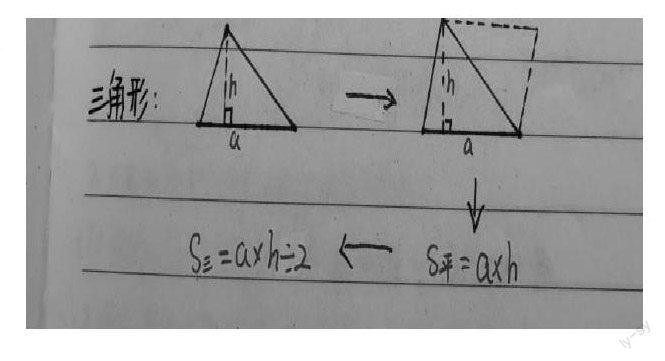
第一类是知识性错误，即学生未完全掌握数学的基本概念，对公式和定理使用不正确，如求三角形的面积时只用底×高，没有除以2就是知识性错误。此类错误需要教师帮助学生有效理清思路，弄清为什么需要除以2。我们是把两个完全一样的三角形拼成一个平行四边形，三角形的底和高与平行四边形的底和高分别相等，所以三角形的面积也就是平行四边形面积的一半，平行四边形的面积=底×高，那三角形的面积=底×高÷2。通过图形和文字的相互结合，帮助学生理解为什么要除以2。

后面再出一组练习：

（1）一个平行四边形的面积是80平方厘米，和它等底等高的三角形的面积是（     ）平方厘米。

（2）一个三角形的底是5厘米，高是8厘米，面积是（    ）平方厘米。

（3）一个三角形的面积是42平方厘米，底是6厘米，高是（    ）厘米。

通过三组练习加强对三角形知识的理解，知道三角形的面积与它等底等高平行四边形面积的关系，能正确地运用公式求三角形的面积，再告诉三角形的面积和底，如何求高，来帮助学生反向思维，加强知识整体性的形成。对于知识性错误，在初步回顾之后，要对出错的知识点进行再分析，把出错的知识点温习一下，尝试找出关于此类知识点中还存在哪些陷阱，同时可以把每类知识点导致的错误尝试整合在一起。

第二类是逻辑性错误，是指学生在分析解决问题的过程中出现错误论证数学概念或定理等。如学生在学习可能性的时候，当连续扔硬币5次都是正面时，教师问：猜一猜下一次会是什么面？有学生认为5次都是正面，下一次反面的概率比较高。此类错误需要让学生明白可能性的本质是什么，每次抛硬币都有可能是正面或反面，正面和反面的可能性相等，并不能因为前5次都是正面，就判断下一次应该是反面了。所以可以继续抛，抛20次，看看此时的结果，再提问：“继续抛下去，下一个呢！”此时，当学生经过自己的实践操作，从潜意识中认识到可能性是相等的。逻辑性这类错误往往是因为学生存在知识盲点，从而导致的分类不当、偷换概念等现象，在回顾时对于分类不当的情况要能够确定每一种解决问题方法的适用范围，记录当时分类错误的原因;对于偷换概念的题型，这类问题是把不同的概念混淆从而导致的错误，回顾时要让学生关注混淆的部分，理清这些部分，做出正确区分。

第三类是策略性错误，即学生在解决问题的过程中未选择合适的解决问题的策略或未建立正确的数学模型从而导致的错误。对于策略性错误，可以分为两个方面，其一是因为策略选择失误导致的解决问题过程过于复杂，比如在求不规则图形的面积时，有的时候可以通过切割平移来转化成规则图形，利用公式来很快解决，有的学生仍然在数整格，数不满整格，时间长而且容易数错。这类问题往往是学生最容易忽视的，在学生看来反正题目做对了，即使烦琐一些也是可以的，我们承认方法的多样化，同时也要强调方法的最优化，要让学生对比多种方法，分析多种方法的优劣，从而选择最合适的方法。其二是因为策略方向出错导致的错误，要让学生分析为什么当时选择这种方法，错在哪里，下次应该怎样避免。

第四类是心理性错误，是指学生由于过度紧张或者其他原因导致的已经掌握的知识、方法使用时出现错误。如高年级学生在计算時太过着急，把30+20的结果写成了600，虽然觉得不可能，但是在梯形面积计算中确有把加法看成乘法的现象。这种错误学生总归结为自己粗心，没有看清题目，可是下次做题时错误继续存在，此类错误要让学生慢下来，仔细审题，写好后要认真检查，养成良好的学习习惯。对于心理性错误，只要简单地回忆一下出错的原因，避免下一次出现类似的错误就可以了。

（三）及时完善并正确分析

在错题本整理过后，如果在其他练习时出现了类似或者一模一样的错误，需要重点关注，可以通过其他形式的记录或其他方式再次整理强化，毕竟落入同一个陷阱两次代表对此类问题的理解还不够深刻，需要再次分析，强化理解，进一步完善。

对于简便计算，教过的教师都知道这个部分学生很容易出错，有的错误今天教师才说过，明天学生又错了，关键在于没有真正理解题目，于是我出了四道题让学生说一说怎么写。下面是一个学生完成的作品：

简便计算

本周，老师让我们试一试如何简便计算675-198，675+198，675-206和675+206。

（1）675-198

首先，判断198更接近哪个整百数，我们就把198看作200，因为多减了2，所以要把2加回来。算式：675-198=675-200+2=475+2=477。

（2）675+198

同样，先把198看作200，但是多加了2，所以需要减去2。算式：675+198=675+200-2=875-2=873。

（3）675-206

有个小朋友是这么写的，675-200+6=475+6=481。我想聪明的读者一定发现了问题：他不仅少减了6，还加了6。我们依照前面的解法算一算：675-206=675-200-6=475-6=469。

（4）675+206

这次要记着，是加法算式，这里的206更加接近整百数200，所以将它分解成200和6。为了简便计算，先用675+200，再用它们的和加6。算式：675+206=675+200+6=875+6=881。

在解决这四题的时候我们发现先要找接近的整百数，多加了就要减、多减了就要加、少加了要再加、少减了要再减。做题时我们要带着理解去做，这样才能做对哦！

当然，错题的分类、整理的方式也是因人而异的，只要采用适合自己的方式，利用好身边的错误资源，发挥出错题应有的价值，进而完善个人的数学思想方法和体系，那一定是行之有效的错题使用策略，也是在“双减”政策下所提倡的最高效的数学学习方法之一。