初中数学不等式模块的教学及解题策略

顾莉

【摘要】不等式是初中数学重要考查部分之一，是初中数学成绩差距的主要知识点.合理地运用之前所学的知识对不等式中的问题进行解决，是初中生应熟练掌握的数学方法.教师应引导学生熟练掌握解决不等式的几种方法，让学生能够熟练地运用不等式去解决数学问题，对学生思维能力和数学文化素养的提高有很大的影响.对不等式知识点熟练的掌握和运用，为学生以后学习数学打下良好的基础，也提高学生的数学思维能力和学习兴趣.

【关键词】初中数学;不等式;题目解答

不等式知识点是初中教学中的一个重难点内容，对学生以后的数学学习有很大的影响.采用多样式的教学方式，使学生成为课堂的主体来激发学生对不等式学习的兴趣.针对性分模块的不等式教学，也让学生数学思维能力得到了锻炼，为以后数学学习提供了新的方法[1].多样式的不等式教学方式，使学生能够合理地掌握和运用不等式.

1 初中数学不等式模块教学策略

1.1 改变教学理念，树立学生主体地位

初中数学不等式模块教学中改变传统的教学理念，让学生成为课堂的主体是提高初中数学不等式教学有效性的基础.教师在初中数学教学课堂上应起引导者的作用，让学生成为课堂的主体鼓励学生去自主探究学习，学生自己探究学习的过程，也加强了学生对不等式的学习和掌握[2].例如教师可以通過利用天平称重来对不等式进行导入，在天平两端分别放入不同重量的书本让学生观察后提问，为什么天平会出现不平衡的情况呢？学生进行自主的思考来思考天平不平衡情况出现的原因，发现因为两边重量不同.教师通过学生自己观察思考来引出不等式学习.改变传统的教学方式，学生去对知识点进行自主的探究学习，更有利于锻炼学生的思维能力和自主学习能力.在自行探究中学到数学知识，也对不等式知识点学习更加充分和具体.

1.2 创设教学情境，激发学生学习兴趣

在初中数学教学课堂中对不等式的讲解中，教师可以采用创设教学情境来激发学生对不等式的学习兴趣.传统的数学教学中教师一般使用“题海”战术，让学生通过大量的习题作业来对知识点进行巩固.教师在学习不等式时，为学生创造一个有趣的教学情境来激发学生对不等式的学习[3].同学们都听过乌鸦喝水的故事，那么乌鸦喝水中也含有不等式的知识点，同学们知道是什么吗？现有一个高为49厘米的量筒，其中的水的深度只有30厘米，乌鸦想要喝到量筒中的水，需要向量筒中放入体积相同的小球.可以看出放入3个小球，水面便上升了6厘米.请同学们进行思考量筒中至少要放入多少个小球时，水才可以溢出，乌鸦才可以喝到水.同学们在有趣的教学情境中激发了对数学学习的兴趣，在乌鸦喝水的故事中，渗透了对不等式知识点的学习，学生的求知欲和思维能力也被激发出来.由图中信息学生可以计算出1个小球可以使水面上升2厘米，没有放小球时水的高度与瓶身相差19厘米.设一共需要放入a个小球，可以得出2a>19.因为放入的是小球所以a只能是整数，a≥10要至少放10个小球乌鸦才可以喝到水.教师通过设计有趣的教学情境来激发学生的学习兴趣，在情景中融入不等式知识点，也提高了学生的思维能力和自主学习能力.

1.3 建立学习小组，培养学生交流能力

在初中教学课堂中教师也可以通过建立学习小组，让学生在交流中对不等式进行更好的学习理解，进而也培养了学生交流组织能力.例如，在一元一次不等式知识点讲解时，教师可以将学生分成学习小组，由小组讨论得出问题的答案.幼儿园有一堆苹果要分给几个小朋友，如果每个小朋友可以分到5个苹果，那么就会有一个得到的苹果不到3个;如果每个小朋友可以分3个苹果，那么苹果又会多出来8个.现在提出问题一共有几个小朋友，又有多少个苹果？在不等式知识点刚开始学习时学生对此类问题思考难免会有疏忽，分成学习小组进行讨论，使每位学生都可以更全面的去思考问题.通过交流讨论来得出问题的答案，使学生之间通过交流对问题的考虑更加的全面具体进而提高了课堂学习效率.通过小组学习能够有效地营造一个良好的课堂氛围，培养学生之间的交流合作能力，对不等式知识点进行更好地巩固学习.

2 初中数学不等式模块题目解答策略

2.1 判断不等式是否成立

在不等式中经常会遇到判断不等式是否成立的问题.题目会给出一个已知的不等式，让学生通过这个已知的不等式和一些题目条件来推断新组成的不等式是否成立.遇到这种问题，教师可以在初中不等式教学课堂中使用分类思想来引导学生如何判断不等式是否成立.

例1 不等式x>y且a为实数，判断下列说法是否正确？

（1）ax

（2）a2x

（3）a+x>a+y一定成立;

（4）ax>ay一定成立.

解析 对于上述问题可以采用分类思想来解决，因为a为实数所以对于a的正负应该分类来考虑.①a为正数时，当不等式两边同乘一个正数时不等式方向不用改变，所以（4）是正确的.不等式两边同时加减一个正数时不等式方向不改变不等式仍然成立，所以（3）也是正确的，（1）（2）错误.②当a是负数时，a的平方是一个正数.不等式左右两边同乘一个正数时不等式方向不改变，不等式仍然成立.所以（2）错误的.不等式左右两边同乘一个负数时不等式方向改变，所以（1）正确，（4）错误.当不等式两边同时加减一个负数时不等式方向不改变不等式仍然成立，所以（3）是正确的.因为题目中并没有说出a是正数还是负数，所以在对a进行探讨时，应充分运用分类思想来多方面考虑.综上所述，无论a是正数还是负数时只有（3）是一定成立的，所以（3）的说法是正确的.

判断不等式是否成立等问题，要对题目中的已知条件进行分类思想处理，充分考虑到问题中所出现的任何情况，对不等式是否成立问题应全面考虑.不等式是否成立此类问题，考验的是学生对不等式的性质是否有明确的定义.要谨记不等式的三个性质：（1）不等式两边同时加上或减去同一个数时不等号方向不变.（2）不等式两边同时乘或除以一个正数不等号方向不变.（3）不等式两边同时乘或除以一个负数时不等号方向改变.充分掌握不等式性质再用分类思想灵活考虑所出现的情况，方能解决不等式是否成立问题.

2.2 比较不等式之间大小

在不等式中比较不等式的大小也是基础题型之一，可以采用化归思想来比较不等式的大小.在解决比较不等式大小问题时，也应熟练掌握不等式的三个性质.

例2 已知a、b、c、d均为正数，且，a2+b2=2c2+2d2求，a+b和2c之间的关系.

解析 结合不等式的性质2，不等式两边同乘或同除以一个正数不等号方向不变，所以我们可以将所求的a+b与2c之间的关系转化成12a+12b与c之间的关系.如图1平行四边形ABCD，假设AC=a，BD=b，由图1可以得出OA=12a OB=12b.在运用三角形的三边关系任两边之和大于第三边，所以我们可以得出AO+BO>AB，由此可以推出12a+12b>c.再根据不等式性质2便可得出a+b>2c.

在不等式比大小题型中充分利用数形结合，将无法直接比出大小的不等式代入到图形中，更能直观地看出不等式之间的大小关系.对于不等式比大小问题，也应对不等式的三个性质进行灵活的掌握，再结合划归思想或者数形结合来解决不等式比大小问题.

2.3 确定不等式字母范围

确定不等式字母范围也是不等式中常考的题型之一，对于这类题型数形结合思想是最直观也是最常用的方法.将不等式的字母范围利用数轴的形式直观的展现，来充分确定不等式中字母的范围.在利用数轴求范围之前教师因为学生先明确数轴的类型和含义，了解数轴几种类型以及数轴所含有的空集和实集.

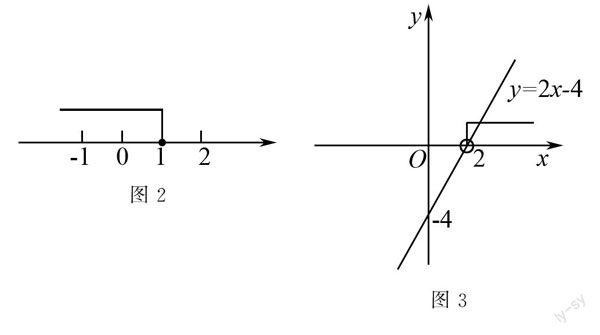
例3 若（a-2）x>a-2的解集如图2所示，求a的取值范围.

解析 根据数轴学生可以得出不等式的解集为x<1.将解集与原不等式联系起来可以发现解集中不等号的方向发生了改变.学生在练习不等式习题时看到不等号发生改变，应及时反映出本题利用的是不等式性质3，是左右两边同时乘以或除以一个负数不等号的方向发生改变.学生要对不等式的性质做到充分的理解和掌握，在任何题型中，能够及时的合理运用不等式性质是解决不等式题型的基础.所以根据不等式的性质三我们看此题可以得出（a-2）<0，进而算出a>2.

在不等式的任何题型中对于数轴的运用十分的常见，学生应充分掌握数轴的画图及表达含义，合理的运用到不等式解题中.数轴属于数形结合思想，数形结合思想是数学问题中常见的一种解题方法，无论是在解决不等式大小问题还是确定不等式中字母的范围，均运用到了数形结合思想.数形结合思想是将数字与几何图形直观的联系在一起，使运用少量的计算由图可以直观地看出问题的答案.对于数形结合思想的合理运用，在不等式解题过程中，需要学生进行充分地掌握和合理的使用.

2.4 寻找不等式存在解集

求不等式的解集是不等式题型中最主要的题型之一，初中对不等式的学习涉及到一元一次不等式，掌握不等式解集的方法是初中不等式学习中主要学习目的之一.在确定不等式解集中一般会采用到两种方法，一是用函数思想来解决不等式解集，二是运用数形结合思想来解决不等式.例5便是使用了函数思想来确定不等式解集.

例4 已知函数y=2x-4的值大于零，求自变量x等于多少.

解析 由题目可以得知y=2x-4为一元一次方程，可以将其转化成一元一次不等式2x- 4>0，运用函数的思想如何解答出不等式的解集？考验的是学生对于函数学习时基础知识的掌握程度，我们将y=2x-4这个一元一次函数画出图像如图3.由图可以看出y=2 x- 4恒过横轴上的（2，0）这一点，求2x-4>0也就相当于求x轴上方所有点的横坐标所构成的集合.

这便是利用函数思想将不等式解集直观的展示在学生面前，可以不通过计算直接得出不等式的解集.利用数形结合思想和函数思想来寻找不等式的解集，可以使不等式解集更直观的展示在学生的面前，可以减少由于计算失误所出现的错误.数形结合思想在不等式题型中运用最为广泛，也是数学解题过程中最常用的一种方法.函数思想来解决不等式解集考验了学生对函数学习基础知识的掌握程度，充分掌握一元一次函数的图像和解析，才能更好地将函数思想运用到不等式解题过程中.

3 结语

总之，一元一次不等式是初中数学学习知识的基础，也是数学教学的重点内容.教师在不等式教学过程中应注重学生对不等式解题方法的锻炼和培养，让学生充分掌握数形结合思想来促进学生对不等式知识的掌握和合理运用，更好地锻炼学生数学思维能力.

参考文献：

[1]邓琦.初中数学不等式的性质教学探究[J].基础教育论坛，2021，（35）：101-102.

[2]孙会会.初中数学不等式教学探究[J].数学教学通讯，2020，（26）：59，66.

[3]茅健美.初中数学不等式题目解答策略[J].數学大世界（下旬版），2020，（8）：79.

[4]柳锡美.两边夹不等式（初一）[J].数理天地（初中版），2005（05）.

[5]林福茂.不等式基本性质和解题方略[J].中学生数理化（初中版），2005（03）.