谈初中数学教学中提升学生解题能力的策略

【摘 要】提升初中学生的数学解题能力具有十分重要的意义，不仅能强化学生的综合素养，还能进一步提高初中数学教学效率。因此，如何实施适时适当的干预，提升学生的解题能力，促进其健康成长，受到了有关部门和学生家长的广泛关注。基于此，文章首先阐述了提升学生数学解题能力的意义，接着分析了解题中学生存在的错误心理以及初中学生在数学解题中存在的问题，最后提出了提升初中学生数学解题能力的策略，以供参考。

【关键词】初中数学;解题能力;提升策略

【中图分类号】G633.6  【文献标识码】A  【文章编号】1671-8437（2022）24-0100-03

解题能力是初中学生全面发展的重要保障，也是学生学习数学必备的技能之一。现阶段，虽然各初中教师已认识到提升学生解题能力的重要性，并注重对学生解题能力的培养，但仍有学生存在错误心理和审题不仔细以及无转换意识的问题。因此，如何提升学生的解题能力已然成为初中数学教学的重中之重。

1   提升学生数学解题能力的意义

在初中数学教学过程中，提升学生数学解题能力的意义主要表现在以下几个方面：第一，可帮助学生养成认真审题的习惯，该习惯不仅贯穿学生的整个学习生涯，还可让学生终身受益;第二，可有效培养学生的逻辑思维能力，并提升其综合运用数学知识的能力，学会多角度看待问题;第三，有利于学生数学综合素养的提升，不仅能提升学生的学习兴趣，使其从被动学习转为主动学习，还能提升学生的表达和交流能力，也可以提升初中数学教学的质量和效率[1]。

2   数学解题中学生存在的错误心理

经研究，在实际数学解题过程中，学生的错误心理可概括为以下两点：第一，意志力薄弱。多数初中学生在解题过程中存在遇到困难就退缩的问题，此类学生对数学的兴趣不大，学习态度较为消极。第二，心理依赖程度较高。部分学生过于依赖教师对于问题的归纳和总结，不仅解题方式单一，还习惯使用固定的解题模式，不仅无法提升自身的解题能力，还形成了思维定势。

3   初中学生在数学解题中存在的问题

3.1  审题不细致，题目阅读能力差

多数初中学生在实际解题过程中会出现求“快”的问题，审题不仔细，常常未明确已知、未知条件就盲目下笔，导致答案出错。同时，还有的学生考虑不全面，较易被题目的干扰因素误导，忽略题目的重要部分，导致答案错误。

以下面这道题为例：（n-1）x?+x=1是关于x的一元二次方程，n的取值范围是下面的哪一项

（   ）。

A.n≠1            B.n≥0

C.n≥0且n≠1      D.n为任意实数

此题考查的是一元二次方程以及二次根式的定义，求解一个包含参数n的不等式组，可分两种情况讨论。可先求二次项系数n-1≠0，但学生通常会疏忽对的分析，从而忽略了n≥0，最终错选A。可见，审题不细致、考虑不全面等问题，会直接影响学生解题能力的提升[2]。此外，初中学生在数学解题方面还普遍存在阅读能力较差的问题，不仅对正常审题造成了阻碍，还严重制约了学生解题能力的提升。具体表现在部分学生很难从文字信息中获取要点，同时归纳重点的能力也不强，导致很难找到解题的突破口。

3.2  无转化意识

如学生在使用等式性质解决相关问题的过程中，若忽视等量可以转化和等量必须转换，或对等式基本性质及其传递性、可加性、对称性运用不熟练，则容易导致解题出错。另外，在使用不等式性质时，学生较易忽略不等式两边同时乘或除一个负数，要改变不等号方向这一性质。同时，在对分式的基本性质进行运用时，学生常常会遗漏分母不为0这一限制。

4   提升初中学生数学解题能力的策略

4.1  强化审题环节，为解题奠定基础

为有效提升初中学生的解题能力，教师应重点提升学生的审题能力，强化审题环节，引导学生捕捉到解题的重要信息。因此，教师要做好以下几点工作：第一，引导学生集中注意力，确保其清晰理解题意，避免学生出现急于求成的心理;第二，引导学生进行粗读、精读和重读，明确题中包含的已知条件和答案之间的关系，挖掘隐藏条件，用笔勾画题目重点，找准问题的切入点;第三，引导学生将题目中的文字部分翻译成数学语言，如依照题意构建直角坐标系等;第四，引导学生完整审题，摆脱思维定势，避免出现审题错误和偏差[3]。

4.2  引導学生运用数形结合思想解题

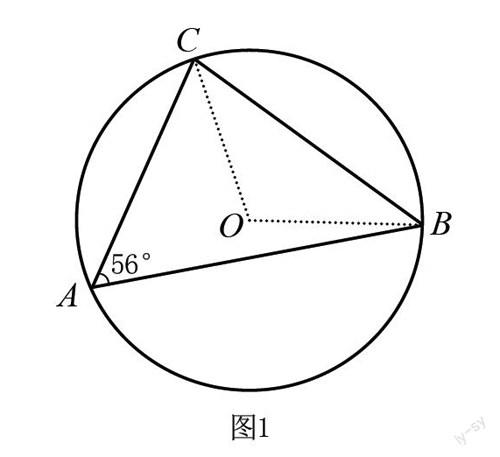
针对初中代数和几何相关的数学问题，教师可通过数形结合的方式进行解题教学，以此提升学生的解题能力。因此，教师需要针对学生开展数形结合思维拓展和训练，在分析题目的过程中，即可依照题意画草图进行分析，这不仅能增强学生分析问题的直观性和全面性，还能使学生系统地理解题目，从而找到解题的切入点[4]。如在解答以下数学问题时，学生即可采取数形结合的方式：已知ΔABC的圆心为O，∠A为56°，那么∠BOC的度数为______。针对以上问题，学生可依照题意画出图1，即可明确解题思路，并快速解答。

4.3  引导学生运用方程思想解题

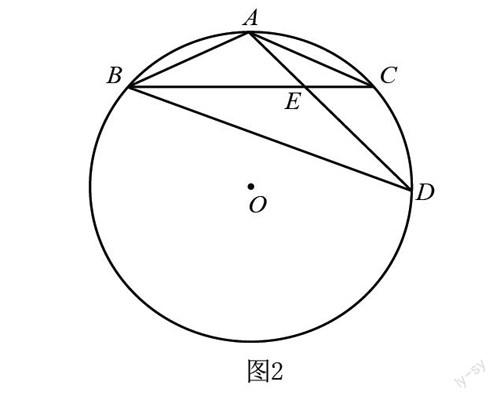
方程思想指通过方程的观点和解方程的方法，分析数学问题中存在的已知量和未知量。与此相关的题目大多侧重于计算，其中几何计算题的占比较大，该类题型主要包含了直角三角形的边角关系、相似三角形的对应边成比例等内容，也可以理解为方程思想的综合运用。因此，教师应在遇到相关典型题目时，引导学生通过方程思想进行解题，以此提升学生的解题能力。以下面这道题为例：如图2所示，⊙O上的四个点分别为A、B、C、D，BC与AD相较于E点，AC=AB，ED=4，AE=2，AB的长为多少？针对此题，教师首先可引导学生证明ΔADB相似于ΔABE，然后根据对应边成比例，通过AB/AD-AE/AB得出AB2=AD×AE=（2+4）×2=12，最后得出AB的长度为2√3。

4.4  引导学生运用分类讨论思想解题

分类讨论的数学思想，也可理解为针对相关数学问题采取分情况讨论的方式进行解答。这一解题方式适用于不同题设下答案不相同的数学题目，教师可引导学生参考题设，将其分为多种情况，并分别进行解答，最后归纳综合各种情况下的答案。以下面这道题为例：如图3所示，A、B为⊙O上的两个点，且∠AOB为100°，其中有一C点在⊙O上，但不与A和B重合，那么∠ACB的度数为多少？首先，应明确该题主要考查圆周角与圆心角的关系，此时需重点注意的是，由于點C在⊙O上，该点有可能在劣弧上，也有可能在优弧上，因此会出现两个答案，此时即可使用分类讨论思想进行解答。可见，分类讨论不仅能有效发挥化零为整思想的作用，还能应用积零为整的整理方式，进一步提升学生的解题能力。

4.5  引导学生运用转化思想解题

在初中数学解题过程中科学运用转化思想，可有效提升学生的解题能力。转化思想不仅是一种重要的思维方式，还充分体现了转化的过程。转化思想的应用具体可分为以下几个方面：①由生疏问题转为熟悉问题;②由抽象问题转为具体问题;

③由复杂问题转为简单问题;④由一般问题转为特殊问题;⑤由高次问题转为低次问题;⑥由未知条件转为已知条件;⑦由整体综合问题转为多个基本问题;⑧由顺向思维转为逆向思维。由此可见，学生科学运用转化思想，不仅能高效实现学习迁移，还能有效提升自身的解题能力，并进一步提升学习质量和效率。如将生疏问题转化为熟悉问题是解题中较为常见的思考方式，即利用所学知识降低新内容的陌生程度，避免因题目的变化而出现解题障碍。以下面这道题为例：如图4所示，已知两圆内切于T点，过T点的直线交小圆于A，交大圆于B，求证TA∶TB为定值。针对此题目，教师同样可以引导学生使用转化思想进行解答，画辅助线连接AA′与BB′，将证明TA∶TB为定值转化为证明平行线对应线段成比例，证明三角形相似即可顺利解答。

4.6  引导学生运用整体思想解题

所谓整体思想，即对相关问题的整体形式、结构以及特征进行分析，从整体出发认识和思考问题，达到化难为易、化繁为简的目的。整体思想具备整体加减、整体代换、整体代入、整体补形、整体改造、整体联想等表现形式，适用于解答方程式与不等式、数与式、函数与图象以及几何与图形等多种问题，不仅能提升学生的思维灵敏程度，还可有效培养学生的解题能力。以解方程2x2+3x-4=为例，在此题的解答过程中，若使用分母求解，会导致过程过于复杂。因此，教师可引导学生依照方程的特点，将方程中的相同部分看作一个整体，使用整体换元的方式，将分式方程转化为整式方程进行解答，以此简化方程及其解题过程，从而实现提升学生解题能力的目标。

4.7  引导学生运用一题多解思想

一题多解即多角度考虑问题，并使用不同的方法解答问题。在解题思路和方法不同时，其解题依据也存在较大的差异。因此，教师应挖掘同一道题的多种解题方法，以此提升学生的解题能力。此种方法既能反映学生对基础知识的掌握情况，还能有效消除学生在解题过程中的依赖心理。以下面这道题为例：两个连续奇数的积为323，求这两个数分是多少。此问题即可一题多解。方法一：设较小的奇数为x，另外一个即为x+2，可列出x（x+2）=323。方法二：设较大的奇数为x，那么较小的奇数即为，可列出。方法三：设x为任意数，那么这两个连续奇数可分别为2x-1和2x+1，即可列出（2x-1）（2x+1）=323。以上方法均可得出两个奇数分别为17、19或者-17、-19。

综上所述，提升学生的解题能力是初中数学教学的重要任务。因此，初中数学教师应明确提升学生解题能力的重要性，并了解解题期间学生的错误心理以及存在的问题，适时适当地指导、干预，引导学生科学运用数形结合思想、方程思想、分类讨论思想、转化思想、整体思想等，以此有效提升学生的解题能力。

【参考文献】

[1]梁芳.初中数学解题能力的培养模式分析[J].新课程教学（电子版），2022（3）.

[2]李权生.初中数学教学中如何培养学生的解题能力[J].新课程，2022（11）.

[3]尹金亮.结合逆向思维，提升初中数学解题能力[J].现代中学生（初中版），2021（22）.

[4]庄炳芳.浅谈初中数学教学中学生解题能力的培养策略[J].考试周刊，2021（65）.

【作者简介】

李娜（1980～），女，汉族，陕西渭南人，本科，中学一级教师。研究方向：初中数学教学。