一年级数量关系的教学方法探究

刘莹

[摘 要]学会分析数量关系是解决问题的关键，只要数量之间的关系明确了，问题便容易解决了。然而，学生对数量关系的理解不是一蹴而就的，必须经历持续有效的发展过程，更不能建立在机械背诵的基础上。只有让学生真正懂得每个量、每个符号的意义，厘清数量之间的关系，才能取得“授之以渔”的功效。

[关键词]一年级;数量关系;问题解决

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2022）17-0079-03

笔者在执教完六年级转而执教一年级后，深知数量关系的教学应贯穿整个小学阶段，而数量关系的启蒙必须从一年级入手。以下是笔者通过一年的教学，对一年级数量关系教学方法的探究。

一、理解关键字符，动态内化数量关系

一年级学生刚入学，数感比较薄弱，这给教学带来一定的困难。鉴于这个原因，部分课堂为了完成教学任务，将学生的“学”变成“记”，将“问题的解决”变成“公式的套用”。如此，当题目一换，学生依然不理解。教师若能从学生的年龄特征出发，借助形象的肢体语言辅助学生理解一些关键字符的含义，可有效促进他们对数量关系的内化。

例如，在教学分与合的知识点时，要让学生理解“分”与“合”的概念，笔者借助肢体语言，让学生在动态学习中内化知识：“合”，即左手有5根手指头，右手有5根手指头，当双手做合十动作时，手指头变多了，所以“合”就是把两部分靠在一起，总数变多了;相反，“分”，即双手做分开动作时，总数分成了两部分，总数变少了。学生跟着反复操作，在做的过程中，就将“分”与“合”的概念进行了内化。

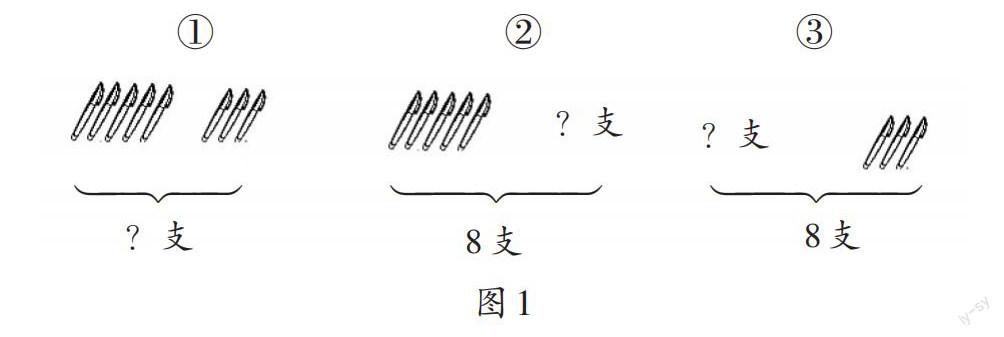
又如，在教学用括线和“？”表示实际问题时，笔者出示三种基础题型（如图1）。

学生解答这三种题型的错误率较高，说明他们没有真正厘清问题和条件之间的关系。针对这样的情况，笔者首先要让学生弄清括线和“？”的实际含义，再借助肢体语言强化理解和记忆。

针对题型①，笔者让学生用手遮住“？”，他们随即发现，左边有5支笔，右边有3支笔。“？”在括线的下面，正是双手合十的情况，求的是“一共”，也就是“总数”，用加法。

针对题型②，笔者让学生用手遮住“？”，知道了“总数”和左边有5支笔，求右边有几支笔。右边是其中的“一部分”，求其中的“一部分”要用减法。

针对题型③，笔者让学生用手遮住“？”，知道了“总数”和右边有3支笔，求左边有几支笔。左边是其中的“一部分”，求其中的“一部分”要用减法。

最后，学生自己概括总结：遮左边，用括线下面的数减右边的数;遮右边，用括线下面的数减左边的数;遮括线下面的数，用左边的数加右边的数。一个简单的遮挡动作，便可让学生迅速分清求“一共”用加法，求其中“一部分”用减法，进而总结出“一部分+另一部分=总数”，将对数量关系的理解能力内化为解决问题的能力。

二、借助已有知识，迁移数量关系

“教”的目的是“放”，迁移就是“放”的一种有效途径。一年级学生的记忆力非常好，对形象知识的理解也更为深刻。于是，笔者抓住学生的这个特征，采用了迁移的教学方法。

1.教材知识的迁移

一图四式是教材常用的模式，只要出现相应的图画，学生就能很快地列出四道算式。可一旦遇到实际问题时，就找不到对应的数量关系。

例如，出示题目：图书馆原有18本故事书，借走了8本，还剩多少本？

学生抓住关键词“还剩”，便能很快在脑海中形成相应的数量关系：原有的本數-借走的本数=剩下的本数。而当笔者对题目稍做修改：图书馆原有18本故事书，现在还剩10本，借走了多少本？一下子就把他们难倒了。此刻，就需要启发学生如何将一图四式的知识点进行迁移。

笔者引导学生主动关联已有知识的经验，不仅让他们顺利打开了思维的闸门，迁移了一图四式的认知经验和方法，还额外收获了新知：

2.生活知识的迁移

笔者听过其他教师分享的一个案例：有一名学生对数量关系的理解十分困难，可当他在自己家开的面馆帮忙收银时，却能很快算出不同顾客不同点餐需求的总价，并正确进行找补。之后，教师将一些解决问题的题目改编成跟点餐有关的题目，该名学生竟能快速准确无误地解答出来。笔者从这个案例中得到启示：利用生活知识进行迁移，可有效帮助学生迁移数学知识。

原题：学校有47个篮球，一年级借走了18个，二年级借走了24个。一共借走了多少个篮球？

改编：妈妈买了47颗糖，姐姐吃了18颗，妹妹吃了24颗。一共吃了多少颗糖？

改编后的题型更接近学生的生活。这不仅教会了学生学习方法的迁移，还教会了学生运用已有知识经验去解决实际问题。

三、手绘简单符号，简化数量关系

课程标准要求学生面对实际问题时，能主动尝试着从数学的角度，运用所学知识和方法寻求解决问题的策略。一年级教材中的很多例题都是以图画或者以图画结合文字的形式呈现，以利于学生理解。如若教师在教学时，再借助简单的手绘，那么学生便会对数量关系理解得更深刻。

例如，“10以内的加法和减法”的教学重点之一是让学生初步体会加、减法的含义。加、减法既是计算的依据，又是解决相关实际问题的基础。

如图2，此题是教材课后的练习题，是学生在初步感知“一部分+另一部分=总数”的基础上，首次用所学知识去解决实际问题。为了让学生形象感知“左边来了1个小朋友”“右边来了2个小朋友”这两个条件与“把两边的小朋友合起来得到什么？”这个问题之间到底存在什么样的关系，笔者在课上请几个学生按照自己的理解上台进行表演。学生表演正确，但当他们从讲台下去回看教材时，又说不清楚了。怎样才能将形象的表演“印”到学生的脑海中呢？于是笔者尝试手绘简单的符号来表示（如图3）。

此时，学生很快明白：当把两部分合起来时就是一个整体，“合起来”的过程用加法。如此，当学生以后遇到类似的题目，便能很快在脑海中“画出”简单的图形，简化数量关系。

如图4，为了让学生体会“总数-一部分=另一部分”，同时能在脑海中自发地抽象出符号来简化各数量之间的关系，笔者让学生自己动手画图表示（如图5）。

学生丰富多彩的想象力跃然纸上。他们都把3个小朋友看成一个整体，用去掉一个图形（或者圈出两个图形）表示从整体中去掉一部分。手绘的过程，是学生获取知识的过程，更是解决问题的过程。

四、联系生活，亲身感知数量关系

课程标准强调数学与现实生活的联系，即数学教学要从学生熟悉的生活情境和感兴趣的事物出发。一年级学生刚从生活走进教材，课堂上教师只要有意识地创设各种情境，就能够很好地帮助学生感知数量之间的关系。

例如，教学连加、连减和加减混合的知识时，笔者出示例题图（如图6）。

要求“一共有多少个南瓜？”，这是学生第一次由一步计算过渡到两步计算。在课堂上模拟运南瓜是不可能的，而让一年级的学生在脑海中将南瓜的数量分为三部分又过于抽象，存在理解难度。于是笔者将南瓜换成教材，并让学生上台表演，学生很快就能看懂其中的数量关系。类似的题型还有车站上、下车人数，停车场进、出车辆等情境，如果都能让学生进行表演，在活动的过程中找出数量关系，感知动作的先后顺序，就能很好地启发学生联系具体情境理解数量关系，同时还能教会学生掌握一定的运算顺序。

又如，教学“认识人民币”时，一年级学生由于缺乏生活经历，很难理解人民币不同面额之间的换算关系。尤其是现在利用电子产品就能完成支付，学生更是很少接触人民币。学生借助图片认识人民币稍易，但使用人民币解决实际问题就难了。可见，创设多种生活情境是必不可少的。对此，笔者让学生带上自己的玩具，标上价格，再让家长帮他们准备一些不同面额的人民币，让学生扮演售货员和顾客进行买卖活动。在生动的买卖活动中，学生逐渐理解：给售货员的钱称为“付出”，物品的价格称为“应付”， 售货员退给的钱叫“找回”，付出-应付=找回，付出-找回=应付，应付+找回=付出。在形象直观、轻松有趣的表演中，学生感知抽象的数学概念，理解买卖中存在的数量关系，有效提高了解决问题的能力。

五、激发检验意识，梳理数量关系

一年级课堂普遍存在教师读一题，学生做一题，读完做完，做完结束，没有留给学生检验的时间。久而久之学生不习惯检验的行为一旦养成，不仅难改，还会对今后的学习产生持续性影响。针对这个问题，教师要重视一年级学生检验意识的培养，让学生经历检验的过程，进而梳理数量之间的关系。

例如，笔者出示一道看图题（如图7）。

师：看图，请列一道加法算式。

生1：4+3=7。

生2：3+4=7。

师：谁的答案对呢？

（学生有说生1的对，有说生2的对）

师：同一幅图，为什么会得到两道算式呢？

生3：4+3表示左边的数量加右边的数量，3+4表示右边的数量加左边的数量，因为题目要求的是总数量，所以两道算式都正确。

师：不管是左边的数量加右边的数量，还是右边的数量加左边的数量，都是“一部分+另一部分=总数”。

交换加数的位置，得数不变。这不仅激起学生思考和探究的欲望，还唤醒他们检验的意识。

又如，一本故事书一共40页，小军已经看了一些，还剩26页没有看。小军已经看了多少页？

生1：40+26=66（页）。

师：他的答案正确吗？

生2：不正确！这本书只有40页，已经看了66页，难道看的页数比书的总页数还多吗？

生3：如果已经看了66页，还剩26页没看的话，那么这本书应该有92页。

生4：这本书一共40页，已经看了66頁，那么和“还剩26页没看”不是矛盾吗？

师：同学们的检验方法真多。那么，你们可以用数量关系式来检验吗？

生5：根据“已看的页码+未看的页码=总页码”可知，66+26≠40。

生6：根据“总页码-已看的页码=未看的页码”可知，40-66没办法减。

师：生1，你能根据你的算式说出相应的数量关系式吗？

生1：总页码+未看的页码=已看的页码。

生（齐）：不对！

师：那么正确的数量关系式应该是什么？

生（齐）：总页码-未看的页码=已看的页码。

在你一言我一语中，数量之间隐藏的关系抽丝剥茧般层层显现，学生的思维也被推向高潮。这样的课堂，是知识发生的课堂，是共生的课堂，更是教师收获硕果的课堂。

综上所述，数量关系的教学要从一年级抓起，从细节处着手。经过一年的实践探究发现，平日里看似简单易操作的教学方法，却也时常被忽略。唯有持之以恒地启蒙引导，才能让学生厘清各种数量关系，提高问题解决的能力。

（责编 覃小慧）