以问导学

白凌晓 谷建琴

问题是数学的心脏。2022年版《义务教育数学课程标准》提出了“强化情境设计与问题提出”的要求。如何依托指向性明确的问题或问题情境引发学生思考，促成深度学习呢？笔者以《平行四边形的面积》教学为例，做具体阐述。

一、以问启疑，猜想公式

教学时，笔者创设了这样一个情境：“全校大扫除中，五（一）班负责清除两个花坛的杂草。班主任将全班学生平均分成了两组，每组承担一个花坛的除草任务。两组同时完成任务后，两名组长都认为自己组负责的花坛大一些。你能帮助他们解决比较两个花坛大小的问题吗？”

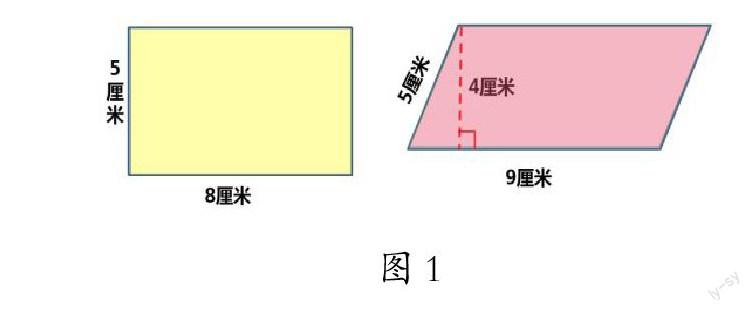
课上，笔者首先给出上述情境，出示没标注数据的长方形和平行四边形的花坛图片，并提问：你知道关于这两个图形的哪些知识？学生结合图形描述了长方形的长、宽、周长、面积，以及平行四边形对边平行，它的高是两条平行线之间的距离等知识。然后，笔者引导：两名组长的争论点是，他们都认为自己负责的花坛大一些，这里的“大一些”具体指什么？学生回答：指面积。笔者提示：比较图形面积，就是看两个图形里各自有多少个同样的面积单位，比一比面积单位个数的多少，你能解决这个问题吗？学生发现还需要知道长方形的长和宽，平行四边形的底、邻边长和高等数据，才能尝试计算。笔者给出相关数据（如图1），并提问：现在能解决了吗？为什么？

学生思考后回答：我们只学过长方形的面积公式，不知道怎么计算平行四边形的面积，还是不能解决问题。笔者追问：通过以往的经验，你觉得平行四边形的面积可能和什么相关？一名学生说：平行四边形的面积公式可能和长方形差不多，应该是把相邻的两条边相乘，其面积是45平方厘米。另一名学生说：我认为平行四边形的面积应该用底乘高计算，是“4×9=36”平方厘米。到底哪一种是正确的呢？笔者让学生想办法证明自己的猜想。

问题情境中“你知道关于这两个图形的哪些知识”等问题，唤醒了学生的已有知识和经验，引导学生通过知识迁移，猜想如何计算平行四边形的面积。这个过程，使学生经历了“图形→数据→面积猜想”的思考过程，促进了挑战性问题“平行四边形的面积是‘底×邻边还是‘底×高”的生成。

二、以问引思，获取公式

在“获取公式”环节，笔者设计了三个问题，引导学生利用割補法计算平行四边形的面积：①你想把平行四边形转化成什么图形，为什么？②你是如何进行剪、拼的？剪、拼过程中需要注意什么？③拼组成的图形和原来的图形有什么相同的地方和不同的地方？什么变了，什么不变？具体教学过程如下。

师：看了大家的展示，你们是想把平行四边形转化成什么图形？

生（齐）：长方形。

师：为什么要剪、拼成长方形？

生1：因为我们学习过长方形的面积，可以利用求长方形面积的方法算出平行四边形的面积。

师：可以把平行四边形随便剪成两部分吗？应该怎么剪？

生2：只有沿高把平行四边形剪开，才能拼成一个长方形;如果任意剪，拼成的图形依然是平行四边形，仍旧解决不了这个问题。

师：沿高剪开，是不是只有一种剪法？

生3：不是，由于平行四边形的高有无数条，我们沿着其中任意一条高剪开都可以。

师：拼成的图形和原来的图形有什么相同的地方和不同的地方？结合你手中的图形，说一说剪、拼前后图形发生了什么变化。

生4：拼之后的图形和原来相比，周长、形状发生了变化，而求面积是求这个平面的大小，剪、拼这个平面，它的面积不会发生改变，拼成的长方形的面积就是原来平行四边形的面积。

师：平行四边形的面积应该如何计算？

生5：通过对比，我发现平行四边形的面积应该用“底×高”计算。

问题①强调转化，让学生说出把平行四边形转化成长方形;问题②突出沿高剪开这一重点，让学生表述自己剪、拼的过程，将思维外化;问题③凸显对比，让学生通过体验将不能解决的问题转变成已知问题加以解决的过程，感悟转化思想。递进式的问题，引导学生获取了平行四边形的面积公式，认识到转化的本质。

三、以问点拨，验证公式

问题设计要注重逻辑性、层次性，也要注重思维的连续性。学生已经用数格子、割补的方法算出了平行四边形的面积，并证实了平行四边形的面积公式，但学生并不清楚公式是如何推导出来的。基于此，笔者设计了两个问题，引导学生从本质上理解公式。

笔者展示剪、拼的动态过程，出示拼组前后图形的对比图片（图略），并提问：转化后的图形和原来的图形之间存在哪些等量关系？学生发现平行四边形的底是转化后长方形的长，平行四边形的高是转化后长方形的宽。笔者继续提问：通过等量代换，我们可以发现转化前后的图形存在几组等量关系？学生思考后回答：转化前后图形面积没变;平行四边形的底和长方形的长相等;平行四边形的高和长方形的宽相等。笔者引导：我们知道S长=长×宽，根据等量关系，你认为S平与它的底和高之间存在怎样的关系？学生思考后回答：S平=底×高。笔者追问：对于平行四边形的面积公式，你还有疑问吗？想一想，为什么平行四边形的面积不能用相邻的两条边相乘来计算？你能用其他办法证明一下吗？经过实际操作，学生对这个问题有了进一步思考，纷纷表述了自己的想法。笔者乘机拿出一个活动的平行四边形框架学具，通过改变其形状引导学生发现平行四边形在变化的过程中，四条边的长度没有改变，但面积一直在变化。笔者适时引导学生总结：平行四边形具有不稳定性，我们没改变它的周长，只是改变了它的形状，它的面积就一直在发生变化，同时发生变化的还有它的高，所以我们可以肯定平行四边形的面积和高相关。“为什么不能用邻边相乘”这一问题启发学生结合实际操作验证平行四边形面积与底和对应的高相关，帮助学生突破了学习难点。

四、以问促用，应用公式

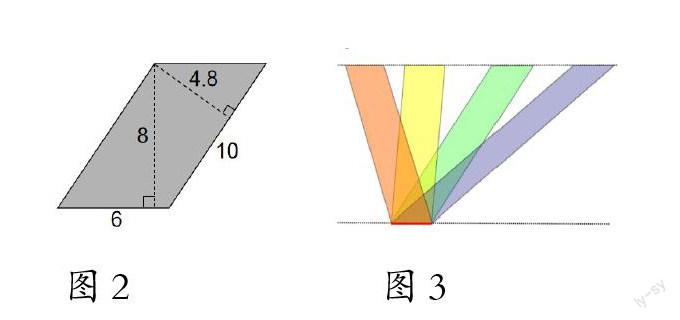
在“应用公式”环节，笔者设计了三个问题：如图2，“6×4.8、10×8、6×8”中，哪一个能正确表示平行四边形的面积？如图3，下面4个图形中，谁的面积大，为什么？你能画一个面积是12平方厘米的平行四边形吗？

这三个问题的难度逐步加大，尤其是最后一个问题，通过给定面积，让学生画平行四边形，促使学生逆向思考平行四边形的面积公式，培养了学生灵活运用知识的能力。每道题完成后，笔者都提问“你认为本题想检验的是有关平行四边形的哪一个知识点”，让学生反思问题解决的过程，进一步巩固知识，明确重难点。

（作者单位：白凌晓，襄阳市教育科学研究院;谷建琴，枣阳市环城中心小学）