有效教学的实施策略
谭又英

高中数学教师如何有效促进学生学习,培养和发展学生数学核心素养呢?
一、改进教学思路,落实教学目标
传统的正弦定理、余弦定理证明的教学中,教师一般遵循“旧教材”的教学路径进行教学,即先在三角形中借助三角形的边角关系、利用“几何法”证明正弦定理后,再用“向量法”证明余弦定理。这样教学,思路不连贯。“新教材”调整为介绍平面向量的概念、运算、基本定理及坐标表示后,展开平面向量的应用。平面向量的应用分为平面几何中的向量方法、向量在物理中的应用举例、余弦定理和正弦定理证明三部分。笔者基于对新教材的理解进行了如下教学。
笔者首先提问:“一个三角形中含有各种各样的几何量,我们在初中已经对三角形的边角关系进行了定性研究,请说一说,你得到了哪些判定三角形全等的方法?”学生回答:“有SAS、ASA、AAS、SSS四种方法。”笔者引导:“这些判定方法表明,给定三角形的三个角、三条边这6个元素中的某些元素,三角形就是唯一确定的。在[?ABC]中,三个角A、B、C所对的边分别是a、b、c,怎样用a和b表示c?也就是说,已知两边及夹角,如何求这个角的对边?”学生思考后提出:“向量的数量积运算中有夹角,可以利用两个向量求数量积来找关系。”学生尝试探究后发现,需要在三角形中写出一个向量的关系式,再进行运算,就能求解。
从表面上看,三角形与平面向量没有直接关系,但是平面向量的加减运算中就有三角形法则,而且学生已经掌握了平面向量的概念和运算。而学生了解了平面几何中的向量方法,会用“三部曲”解决平面几何中关于长度、夹角等问题,便能用向量方法证明出余弦定理。
二、抓住典型问题,促进自主探究
“以学定教”能激发学生的求知欲,培养他们的探究精神、创新能力及应用意识,使学生真正成为学习的主体。笔者以一道典型易错题的教学为例,谈一谈如何促进学生自主探究。
笔者首先出示例题:已知平面四边形ABCD,AB=BC=3,CD=1,[AD=5],AD垂直DC。沿直线[AC]将[?DAC]翻折成[?][D'AC],则[AC?BD']= ;当平面[D'AC]垂直平面[ABC]时,异面直线[AC]与[BD']所成角的余弦值是 。由于这道题的正确率很低,笔者依据学生的错误原因和现有知识基础,在讲评之前给学生布置了一个任务——课外按题目要求绘制出平面四边形并进行翻折,思考如何解题。学生结合题目所求问题,探究[?DAC]翻折成[?D'AC]时线与线、线与面位置关系的变化,结合向量知识自主寻求解决办法。
课堂上,笔者与学生进行了如下互动:
师:你们做出了平面四边形ABCD,并沿直线[AC]将[?DAC]翻折成[?D'AC]。你在翻折过程中有什么发现?
生1:翻折后,[BD']是空间中的一条线,它与直线[AC]是异面的,但是第一问没有说明[?DAC]翻折到什么位置。
生2:题目没有说明具体位置,我们可以在平面[D'AC]垂直平面[ABC]时求解。
生3:我认为无论[?DAC]翻折到何处,[ AC?BD']总是一个定值。
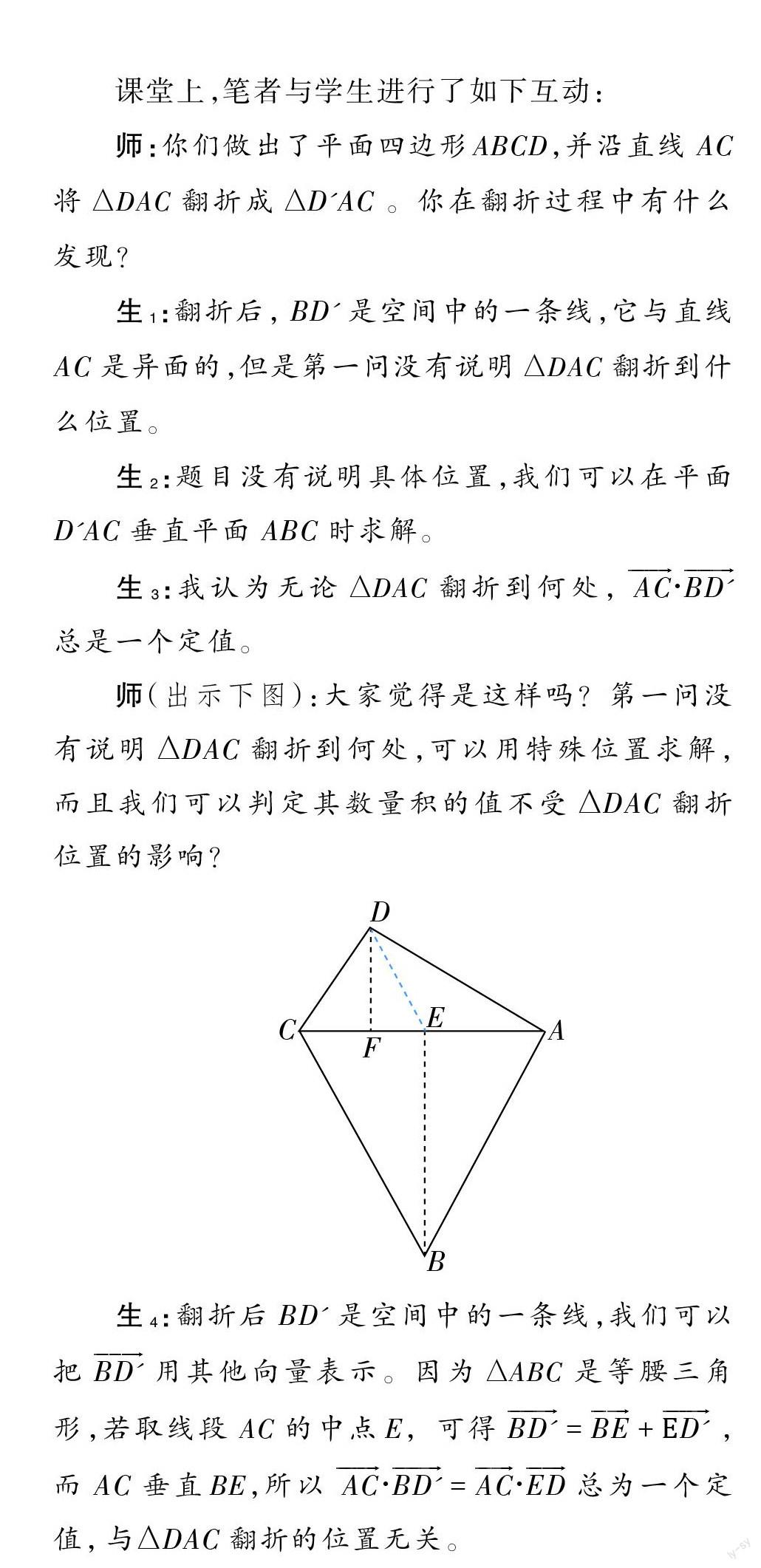
师(出示下图):大家觉得是这样吗?第一问没有说明[?DAC]翻折到何处,可以用特殊位置求解,而且我们可以判定其数量积的值不受[?DAC]翻折位置的影响?
生4:翻折后[BD']是空间中的一条线,我们可以把[BD']用其他向量表示。因为[?ABC]是等腰三角形,若取线段[AC]的中点E, 可得[BD'=BE+][ED'],而[AC]垂直BE,所以[ AC?BD'=AC?ED]总为一个定值,[与?DAC]翻折的位置无关。
生5:我是以点E为坐标原点,利用平面[D'AC]垂直平面[ABC]建立空間直角坐标系。这样两个问题就可以一起解答。
以上教学,教师放手让学生自主探究问题,激发了学生学习的积极性。学生利用模型操作探究,通过观察、比较、分析发现题目所蕴含的规律,找到了解决问题的多种途径。
三、依托信息技术,促进深度理解
“数形结合”是解析几何中重要的数学思想。教师在授课时借助希沃白板里的学科工具,在授课界面利用尺规、几何图形等制作动画效果,能帮助学生直观认识直线和圆的位置关系。
课堂上,笔者先进行情境导入:“一艘轮船在沿直线返回港口的途中接到气象台的台风预报:台风中心位于轮船正西80km处,受影响的范围是半径为30km的圆形区域。已知港口位于台风中心正北40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?”部分学生没有准确运用问题中的数据,只是大概画出台风中心、轮船和港口的位置,这样无法得出确切结果。笔者请一名学生进行展示,学生在希沃白板授课模式下,利用“更多”工具中的尺规,以台风中心为圆心,3cm长为半径画圆,轮船位于台风中心正东方向8cm处,港口位于台风中心正北4cm处,将港口和轮船的位置标出来,并用直线连起来,很清楚地展示出直线与圆的位置关系,得出它们没有公共点,即轮船在航行过程中不会受到台风的影响。通过白板展示,最开始没有得出确切结论的学生也发现了自己的问题所在,即没有准确运用问题中的数据。通过探究,学生明确了这个实际问题本质上是要判断直线与圆的位置关系。
通过进一步交流,师生共同归纳、总结出三种直线与圆的位置关系:相交、相切、相离。笔者利用白板动态演示直线从远处慢慢靠近圆的过程,然后提问:请你通过动图观察直线逐步向圆靠近的过程中,这三种位置关系的变化,说一说这些位置关系在图象中表现出什么特点?一名学生回答:直线l与圆C相离时,没有公共点。另一名学生回答:直线l与圆C相切时有一个公共点,相交时有两个公共点。
本节课的情境导入,教师选择实际生活中的台风、轮船等元素,让学生对解决问题产生兴趣。教学过程中,教师利用多媒体把复杂的数学问题变得简明、直观,引导学生在利用代数方法解决几何问题的过程中体会到数形结合思想的运用价值。
(作者单位:洪湖市文泉中学)
责任编辑 张敏

