高中数学教科书“阅读材料”的教学与思考
陆娅君 冉胜利 张和平
[摘 要] “阅读材料”是开展探究性学习的重要素材,文章基于“抛物线的光学性质及其应用”内容开展教学并反思:将“阅读材料”融入课堂教学,有利于数学思想方法的渗透以及培养学生的数学应用意识和探究问题的能力.
[关键词] 数学教科书;阅读材料;抛物线的光学性质
《普通高中数学课程标准(2017年版)》指出,教学活动不应只限于讲授和练习,还应倡导阅读自学、独立思考、动手实践、自主探究、合作交流等学习数学的方式[1]. 教材中的“阅读材料”体现了教学内容的弹性,符合不同层次学生的发展,能帮助学生掌握正文内容;并能促使学生内化数学思想方法、培养学生的数学应用意识和探究问题的能力. 基于“阅读材料”的教学是一种高质高效的教学方式,能够切实实现教学效率和教学质量的提高[2]. 但在实际教学中,教师对阅读材料的使用仅仅停留于读一读、看一看,缺乏深度和广度,不能有效地发挥其功能与价值. 基于此,本文选取新人教A版高中数学教科书“阅读材料”中的“抛物线的光学性质及其应用”进行教学探索,谈谈对阅读材料的使用与思考.
[?]案例分析
1. 阅读发现
太阳灶是利用太阳光照射,通过聚光获取热量,进行加热的一种装置. 它不需要燃烧燃料,上面装有能旋转的反射镜,反射镜的形状是抛物面(如图1所示),利用这样的装置就能进行炊事烹饪.
师:利用太阳灶进行炊事烹饪的原理是什么?
生:因为曲面形的反射镜将光线汇聚在一点进行加热.
师:这个反射镜的轴截面是一个怎样的图形?盛食物的容器应该位于哪个特殊的位置?
生:可能是抛物线,容器位于抛物线的焦点.
设计意图:依托“太阳灶加热”创设情境,体现数学知识的广泛应用,接着引导学生对其工作原理进行解释,抽象出抛物线模型,感受数学在日常生活中的应用价值. 教师再结合抛物线的相关知识进行设问与回答,进一步将生活问题抽象为数学问题,让学生直观感受抛物线中光波的反射规律与焦点有关,提升学生数学的感知能力和数学抽象的核心素养.
2. 直观验证
问题1:光的反射现象如果与抛物线的焦点有关,那么应该遵循怎样的反射规律?
在物理学中,焦点可以理解成光线聚集的点. 把太阳灶装置中反射镜的轴截面抽象成抛物线,把水壶的位置抽象成抛物线的焦点,把光线抽象成直线,得到图2. 图2直观地反映了光在抛物线内的反射规律:一束平行于抛物线的轴的光线,经过抛物线的反射集中于它的焦点.
问题2:反射镜面与抛物线会有怎样的位置关系?
由物理学的相关知识可得,反射镜面与抛物线的位置关系是相切的.
问题3:如何直观地验证抛物线中光的反射规律?
可以利用几何画板直观验证:首先找到抛物线的一条切线,作为反射镜面;连接点M和切点P,MP平行于抛物线的对称轴,MP就可以作为一条入射光线;作出反射镜面的法线PH后,就需要观察反射光线是否经过点F,如图3所示.
问题4:用几何画板直观演示当点P在抛物线上运动时,∠MPH和∠FPH会有怎样的数量关系?如图4所示.
当∠MPH=∠FPH时,也就说明反射光线经过点F. 改变抛物线的形状,可以发现这两个角仍然是相等的.
设计意图:根据生活现象猜想出光在抛物线内的反射规律,再用几何画板直观验证,尝试建立文字与图形的联系,促使学生透过现象看数学本质. 经历数学知识抽象的过程,培养学生数学模型思想,发展学生数学抽象、直观想象的核心素养.
3. 深度探究
师:利用几何画板初步验证了光在抛物线内的反射规律,如何从数学的角度来证明?
活动:已知定直线l和定点F(定点F不经过定直线l),在定直线l上随机取一点A,如图5所示. 如何通过纸片对折的方式作出线段AF的垂直平分线?
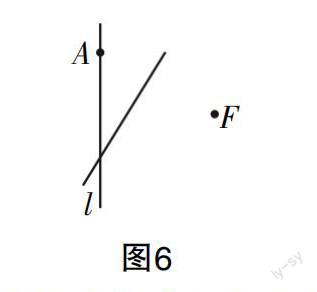
生:通过对折让点A和点F重合,由此便得到一条折痕,将折痕用笔画上颜色即得线段AF的垂直平分线,如图6所示.
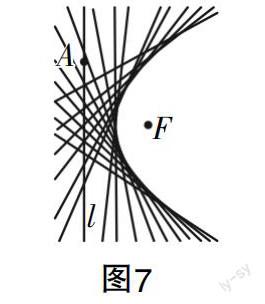
师:在定直线l上取无数个点,一直重复此操作过程,有什么发现?如图7所示.
设计意图:让学生动手操作折纸活动,培养学生动手实践、合作交流、自主探究的能力;使学生在操作、观察、猜想的过程中,逐渐领悟折痕所在直线与抛物线的位置关系,自主构建认知结构. 通过数学活动让学生体验从具体到抽象的过程,促使学生透过现象看数学本质,感悟数学思想方法,培养学生直观想象、数学抽象的核心素养.
师:折痕所在直线和抛物线具有怎样的位置关系?
生:通过折纸活动发现折痕所在直线与抛物线是相切的.
师:设折痕所在直线为m,如果m和抛物线相切,那么直线m会作为一个什么图形出现?
生:直线m会作为反射镜面出现,但通过“折纸”活动和几何画板的验证得到的“相切”是不严谨的,需要进一步证明.
问题5:如何证明折痕所在直线m与抛物线相切?
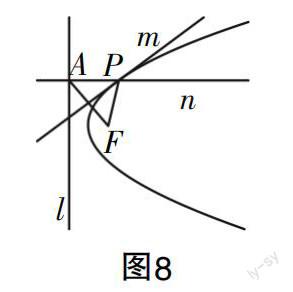
生:首先证明点P在抛物线上. 如图8所示,过点A作直线l的垂线n,垂足为A,直线n与直线m相交于点P;将PF连接起来,因为点P在线段AF的垂直平分线上,由垂直平分线的性质可知PA=PF,即点P在抛物线上.
师:點P既是抛物线上的点,同时也处于线段AF的垂直平分线上,那么也只能说明点P是直线m与抛物线的一个交点,交点一定是切点吗?相交和相切最主要的区别是什么?
生:相交和相切最主要的区别是交点的个数问题. 如果要验证相切的情况,就需要验证点P是直线m与抛物线唯一的交点.
师:如何证明一个点的唯一性?
生:在直线m上任意取一个不与点P重合的点N. 过点N作直线l的垂线,垂足为B,如图9所示. 因为点A,B,N不在同一条直线上,且NB⊥l,故点A,B,N可构成一个直角三角形. 根据直角三角形的性质可得AN>BN. 因为点N在线段AF的垂直平分线上,根据垂直平分线的性质可知AN=FN. 根据等价替换可得FN>BN,据此说明点N到定点的距离大于到定直线的距离,即点N位于抛物线的外部. 因此,直线m上有且只有一个点P在抛物线上,所以直线m与抛物线相切,点P是切点.
问题6:如图10所示,已知直线m是线段AF的垂直平分线,AM⊥l于A,PH⊥m于P,如何证明∠MPH=∠FPH?
生:因为直线m是线段AF的垂直平分线,所以
,据此可得△CPF≌△CPA,即∠CPF=∠CPA. 因为∠CPA=∠DPM,由等量替换可得∠CPF=∠DPM. 因为PH⊥m,所以∠CPH=∠DPH,所以∠MPH=∠FPH.
据此可得抛物线的光学性质:一束平行于抛物线的轴的光线,经过抛物线的反射集中于它的焦点.
设计意图:通过几何画板和折纸活动验证抛物线的光学性质还不够严谨,需从数学的角度证明折痕所在直线与抛物线相切及∠MPH=∠FPH,从而抽象出抛物线的光学性质,体现了数学学科结构严谨、逻辑性强的特征,培养学生数学抽象、逻辑推理的核心素养. 借助图形进行证明,体现了数形結合思想方法,培养学生直观想象的核心素养.
4. 巩固拓展
问题7:在问题情境中,利用太阳灶加热水或食物时,为什么要将反射镜设计成抛物面的形状?盛食物的容器应该位于哪个位置?为什么?
问题8:在手电筒内,小灯泡后面的反光镜为什么要设计成抛物面的形状?小灯泡的位置应该在哪里?为什么?
设计意图:对情境内容再次提问,帮助学生梳理知识脉络,更加清晰地认识抛物线的光学性质在太阳灶中应用的具体原理. 通过相似问题,让学生进一步巩固抛物线的相关知识,感受“抛物线的光学性质”在生活中的广泛应用,开阔学生的数学视野.
[?]对“阅读材料”的思考
1. 对案例的总结与反思
基于教材中的“阅读材料”创设情境,由此引入课题和提出相关的探究问题,接着利用折纸活动和几何画板验证抛物线的光学性质,培养学生动手操作、自主探究的能力,积累数学活动经验,进而发展学生直观想象、数学抽象的核心素养;再用数学方法证明性质,让学生经历完整的数学论证过程,感悟数学严密的逻辑性,培养求真务实的学科精神;最后让学生理解抛物线的光学性质在某些装置中的应用原理,培养学生的数学应用意识.
2. 渗透数学思想方法
“阅读材料”蕴含了丰富的数学思想方法,如“探究指数函数的性质”中介绍了利用指数函数的图像探究其性质,图像直观地展现了随着底数a(a>0,a≠1)的变化,函数图像也在动态变化的过程,学生能较容易地发现指数函数的性质,感受数形结合的思想;《牛顿法——用导数方法求方程的近似解》中介绍了利用逼近法求方程的近似解,体现了极限思想. 教师应当深入剖析“阅读材料”的数学本质,并合理运用其进行教学,更好地帮助学生内化数学知识,掌握数学方法.
3. 培养数学应用意识
教材中“阅读材料”的内容与社会生活、科技生产等有着紧密联系. 教学中教师应引导学生从数学的角度观察生活,感受数学在生活中的应用价值以及培养学生的数学应用意识. 如“向量概念的推广与应用”让学生了解到能利用n维向量表示生活或科学研究中的许多量,并利用向量理论研究其性质;“圆锥曲线的光学性质及其应用”介绍了手电筒发光和电影放映机的工作原理,从而让学生感受数学的应用价值,感悟生活处处皆数学.
4. 培养探究问题能力
“阅读材料”设置了“信息技术应用”专题,其目的是希望教师尝试利用网络资源开展基于信息技术的教学,引导学生把信息技术作为学习数学和解决问题的工具. 在运用数学软件探究问题的过程中,学生经历发现问题、提出猜想、独立验证等过程,可以培养学生探究问题的能力. 如“用信息技术探究点的轨迹:椭圆”“用计算机绘制函数图像”“图形技术与函数性质”等都是可以使用信息技术进行探究性学习的素材.
教材中的“阅读材料”蕴含着丰富的教育功能,教师应当主动挖掘这些资源,进行再创造、再组织,应用到课堂教学中,让学生在此过程中感受数学的魅力与价值.
参考文献:
[1] 中华人民共和国教育部. 普通高中数学课程标准(2017年版)[M]. 北京:人民教育出版社,2017.
[2] 米秀旭. 基于教材中阅读材料的数学核心素养培养[J]. 上海中学数学,2018(Z1):13-14+21.

