基于线性规划数学模型的连铸切割优化

鲁明浩 陶琪 王宁宁

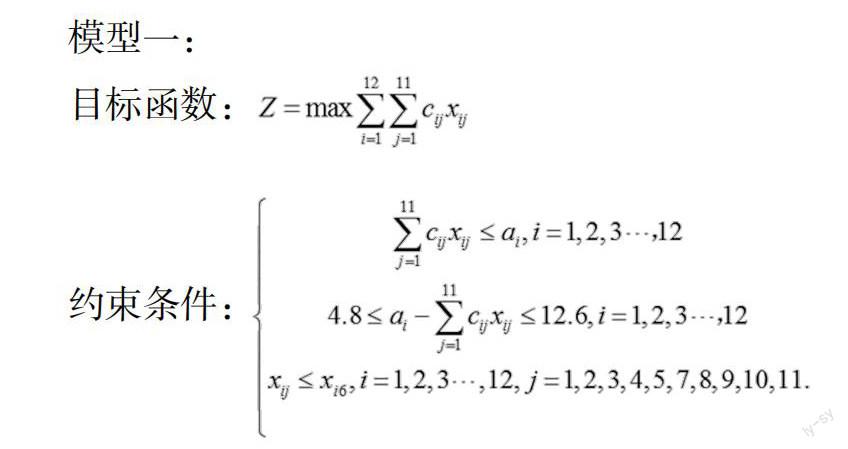
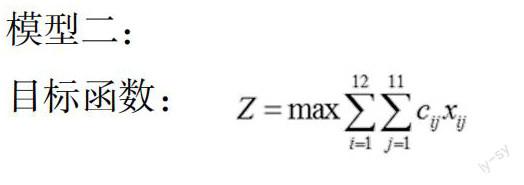
摘要：当数据较大或种类繁多时，人们利用LINGO线性规划软件进行优化设计，不但操作简单，而且结果准确。文章以2021年全国大学生数学建模竞赛专科组D题为例，介绍了基于LINGO线性规划软件的连铸切割设计方法。

关键词：线性规划;连铸切割;LINGO软件

自1947年丹齐克提出求解线性规划的单纯形方法以来，线性规划在实际生活中的应用日益广泛，特别是在计算机软件能处理多个约束条件和决策变量的线性规划问题之后。2020年2月，高兰芳将线性规划方法引入工程投资分配，寻求解决多方案投资决策中资金分配优化路径，建立线性规划模型求得最优解，使得投资收益最大化。2020年9月，郑彩云等人对企业运输问题进行研究，建立线性规划模型，并运用MATLAB软件编程计算方法求解，在供给和需求保持平衡的同时，制订出相关的流量和流向，从而降低了运输成本;2020年12月，郑文魁等人以某大型土方场平工程为例，介绍了基于LINGO线性规划软件的土方调配设计的原理和方法。

近年来，建筑业、制造业等行业的发展，对钢铁产品的需求日渐增加，钢铁领域迎来了更多的发展机遇。连铸是将钢水变成钢坯的过程，钢水经过结晶器时，长期使用会发生结晶异常，以此切割出的钢坯则为报废段。因此，如何减少损失，成为钢铁生产者关注的主要问题，也是企业生产线制定策略的主要参考依据。基于此，笔者以2021年全国大学生数学建模竞赛专科组D题第一问的数据为基础，分析了钢铁生产连铸切割过程中容易出现的损失情况，并构建了基于线性规划的数学优化模型，借助LINGO软件求解，得到最优切割方案，从而为建筑业、制造行业等企业制定连铸切割方案提供了重要依据。

一、问题描述

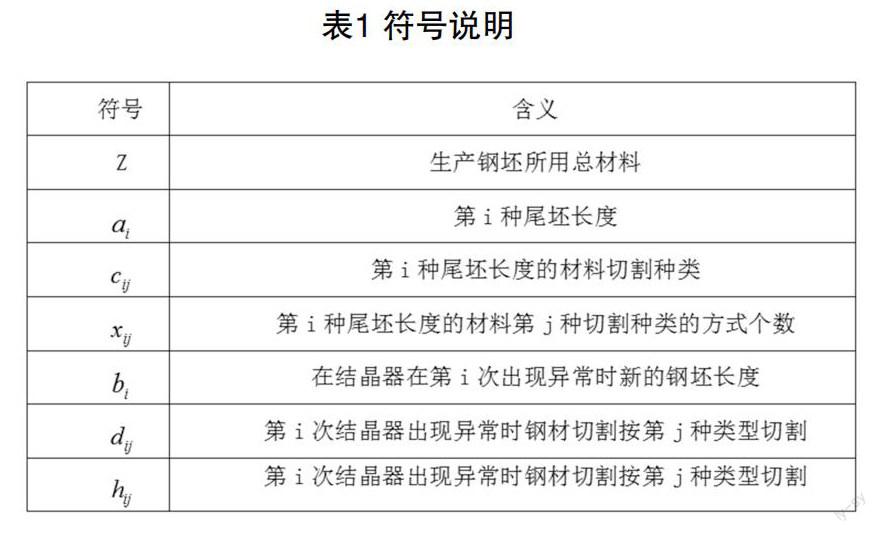
假设用户的目标值为9.5米，用戶要求范围为9至10米，给定尾坯长度109米、93.4米、80.9米、72米、62.7米、52.5米、44.9米、42.7米、31.6米、22.7米、14.5米和13.7米。假设钢坯在切割过程中没有产生磨损、切割后的长度不受热胀冷缩的影响，从尾坯长度、切割方案、切割损失三个方面考虑给出具体的钢坯最优切割方案。符号说明如表1所示。

二、基于线性规划的数学优化模型

（一）模型探究

在考虑尽量减少切割损失的前提条件下，根据基本要求，切割长度必须处于4.8至12.6米，过短或者过长都无法转运。此外，在相同的切割损失下，钢坯切割出的尺寸大小尽量满足用户的要求，即切割长度9.5米的个数最多，因此建立模型一。

模型一：

目标函数：

约束条件：

依据模型一，借助LINGO软件进行求解，结果如表2所示。

根据附录中的正常要求，并结合实际情况分析，切割钢坯时应尽量满足用户要求的长度9.5米，所以在切割过程中，以目标值9.5米为首要切割长度。切割总长为22.7米和13.7米时，其切割损失长度无法满足基本要求中的4.8米至12.6米，无法移动，对生产过程产生影响，所以需要独立讨论。在钢坯长度为22.7米和13.7米时，满足钢坯将进行二次离线切割的基本要求，所以22.7米可以切割出目标值9.5米一段，10米一段;13.7米时，可以切割出目标值1段。

（二）模型优化

对于模型一，虽然结果可观，但是对客户的需求考虑不够。在现实生活中，人们对钢材原材料的需求在不能满足最佳要求时，更倾向于接近材料的目标值，所以首先要考虑目标值9.5米，其次为9.6米、9.4米，从而对模型进一步优化，建立模型二。

模型二：

目标函数：

约束条件：

依据模型二，借助LINGO软件进行求解，得出模型的最优方案，最终结果如表3所示。

观察表3中的数据可知，目标长度9.5米的个数最多，9.5米左右的次之。当钢坯总长度为80.9米时，其目标长度个数达到最大值。只有钢坯总长度为52.5米时，其目标长度个数为0个。

笔者从所给定钢坯数据、参数要求、用户需求出发，构建了线性规划数学优化模型模型，并应用LINGO数学软件求解模型，得出钢坯最优切割方案，使得损失最小化，用户需求目标值最大化，为建筑业、制造行业等企业制定连铸切割方案提供了重要依据。

参考文献：

[1]高兰芳.基于线性规划的工程投资分配模型及优化[J].四川轻化工大学学报（自然科学版），2020（1）.

[2]李彩玉，陈见标，邓漫红，等.基于线性规划的运输策略优化研究[J].中国储运，2020（9）.

[3]郑文魁，巫昌斌，刘德辉.基于LINGO线性规划的土方调配设计[J].人民黄河，2020（S2）.

[4]邓朗妮，罗日生，郭亮，等.基于线性规划数学模型算法的土方调配[J].土木工程与管理学报，2018（2）.

[5]程琳.围绕数学核心素养的数学教学活动——以“简单线性规划”为例[J].理科爱好者（教育教学），2020（5）.

[6]王禹.注重数学理解 提升思维能力——以“线性规划”教学为例[J].上海中学数学，2019（Z2）.

[7]李艳，徐章韬.核心素养背景下数学教学中渗透思想教育的探索——以线性规划一课为例[J].数学通讯，2019（12）.

[8]朱晴.浅谈与专业相结合的高效数学课堂——基于《线性规划》教学的个案研究[J].读与写（教育教学刊），2018（1）.

[9]袁利江.基于线性规划的角度探讨含双参数的数学问题[J].数学教学通讯，2012（12）.

基金项目：2021年全国职业教育科研规划课题“基于课程思政的高职数学教学研究”阶段性成果，项目编号：2021QZJ065。

（作者单位：陕西工业职业技术学院）