农村金融发展对农村农业科学技术发展的支持作用

宋学林

针对山东省农村金融发展规模与山东省农业科技进步贡献率之间的关系，本文采用格兰杰因果检验的方法，而鉴于格兰杰检验的条件，本文采取单位根检验、VAR模型、Johansen 检验等方法，得出了相应的结果。

变量选取与研究方法说明

为了验证金融发展规模与农村农业科学技术发展之间的因果关系，本文以山东省为例，拟采取格兰杰因果检验分析法予以验证。进行格兰杰因果检验分析的一个重要数学前提是，假设系统内部存在的每个变量数据之间只存在一个数据协整关系问题（即是否存在长期均衡）。而我们若一定要去严格地进行一个数据协整性的检验，需要首先对其每个变量数据间进行的时间单位根关系的因果检验，以最终帮助人们判定该变量数据间具有的一个数据平稳性。如果检验所得出的结果序列不平稳，那么我们则往往还会根据需要判定其结果的时间序列是否某一个平稳单整的时间序列，这也就是说一个时间序列可以是一个平稳时间序列或者是平稳时间序列的平稳单整时间序列。两个检验的条件下必须具有其一时才能进行平稳协整序列的检验。对变量进行单位根的检验，本文中我们选取使用的方法是ADF检验法。

一、变量选取

考虑到山东省作为农业大省的农村发展实际以及《山东省统计年鉴》的数据情况，本文选取了以下几个指标作为参考：

1.农村金融发展的相应规模和指标，本文中用FGM表示。

如果我们用BFI表示金融组织和金融机构的农村贷款余额，用CGDP表示农村的GDP[鉴于《山东省统计年鉴》的数据情况，我们以山东省的农村农业相关产业（农、林、牧、渔等）为代表，近似地替代该数据]，那么我们就得到表示式：（1）

2. 农村金融发展的效率，本文中用FXL表示。

如果我們用RDB表示农村存款余额，用LRD表示农村贷款余额，那么我们得到表示式： （2）

3.农村金融结构指标，本文中用FJG表示。

如果我们用AL表示农业贷款额，用TL表示山东省总贷款额，那么我们得到表示式： （3）

4.农业科技进步指标，本文中用JSL表示。则：JSL=农业总产值增长率―物资费用产出弹性×物资费用增长率―劳动力产出弹性×劳动力增长率―耕地产出弹性×耕地增长率。

通过反复查阅各种相关技术资料，我们将得到山东省的各种相关经济数据，然后我们把其公式带入柯布―道格拉斯生产弹性函数的公式中（式中的K、L、M分别代表物资费用、劳动力和耕地面积），文中指标计算的时间范围为2007年至2021年，共15年。其中山东省农业生产总值、土地耕种面积、农业生产劳动力这三项时间序列都是通过查阅《山东省统计年鉴》得到，具备权威性;而物资费用数据是通过查阅《中国农村统计年鉴》得到，权威性也很高。为了同时求得测算函数中各农业区域的耕地平均农业物资费用、劳动力弹性值和全国人均拥有耕地弹性值，我们尚需首先假设，即平均农业规模报酬弹性为不变。通过反复仔细研究查阅国内外各种农业相关经济计算分，我们预计能给出得到的如下弹性测算的结果：

全国农业物资费用弹性值约为，农业劳动力弹性值约为，耕地面积弹性值约为。

由于土地耕种面积在相对较短的时间内变化幅度小，甚至小到几乎可以忽略不计，因此在考虑到数据可得性的基础上，我们用全国的农业耕种土地面积弹性值来代替山东省的耕地弹性值对山东省农村农业科学技术进步率进行测算;而对于物资费用弹性（），我们通过下述公式进行调整 。

由于，而，故，因而在计算出山东省农业物质费用弹性值后，根据公式即可求出劳动力弹性。通过相应计算，农业生产物资费用、农业生产劳动力、土地耕种面积弹性值的近似值分别为0.612、0.138、0.250。通过进一步计算，我们就得出了山东省农村农业科学技术进步率及贡献率。

实证硏究方法说明

一、时间序列平稳性的单位根检验

一般说来，各变量间的关系规律是不是随时间改变而发生相应的变化，是判断时间序列是否平稳的重要依据。正常来说，平稳的时间序列可以直接进行自回归;对于非平稳的时间序列，为了使回归结果更加理想，我们需要看时间序列是否存在单位根，而要到这一步结果，我们需要进行单位根检验。

在进行了单位根检验的各项检验假设工作之后，我们必须进一步对其实验所得结果再逐一进行一次综合比较分析，要去重点地看一下在各个检验假设变量中取的ADF的值，以及在我们所选取到的那个最大的临界值。具体地说，就是看选取的ADF值与最大临界值的大小关系：如果选取的ADF值在临界值的绝对值之内，则这个变量有单位根就是非平稳的;如果选取的ADF值超出了临界值的绝对值，则这个变量没有单位根。如果变量非平稳，则需要进行一阶差分，重复这个过程，直到变量平稳为止。

二、协整检验

进行协整检验的目的是验证两个变量之间的比例关系是否稳定，这种稳定不是这两个变量各自的稳定，而是二者之间的相对稳定。也就是说，这种稳定包含两种含义：一是这两个变量各自稳定，二是这两个变量都不稳定，但它们的变化方向和变化幅度却都是一致的，故而相对比例是稳定的。

三、格兰杰因果检验

在单位根检验并进行了相应平稳性处理的基础上，进行协整检验，通过了协整检验之后，我们就需要进行格兰杰因果关系检验。格兰杰检验的目的是检验两个相互独立的变量是否具有因果关系，因而，格兰杰检验的结果很简单，只有两个：要么通过检验，说明两个变量之间具有因果关系，我们可以进行下一步的脉冲响应和方差分解;要么通不过检验，说明两个变量之间没有因果关系，那么研究到此终止，因为对于两个没有因果关系的独立变量继续进行研究也没什么意义。

实证分析

一、单位根检验

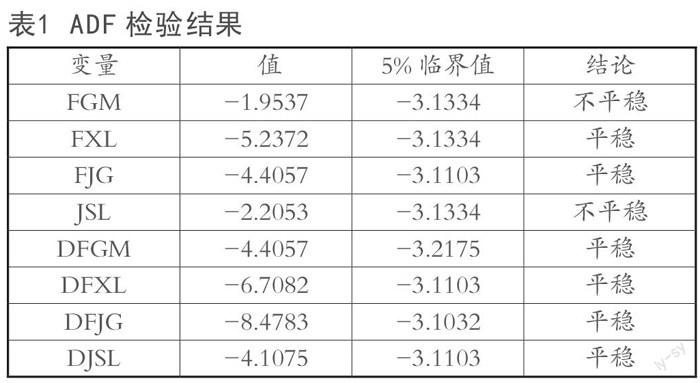
首先，对变量进行单位根检验。由表1我们可知：FGM和JSL（也就是山东省的农村金融科技经济发展规模、农业科技社会生产力进步贡献率）的实际ADF值在临界值的绝对值之内，那么说明这两个变量有单位根，是非平稳的。接着我们需要进行一阶差分计算，一阶差分之后这两个变量的ADF值超过了临界值的绝对值，这说明在进行了一次一阶差分之后这两个变量就变得平稳。而对于另外两个变量FXL和FJG（也就是山东省目前我国重要农村金融经济领域发展速度及整体效率）的实际ADF值超出了临界值的绝对值，说明这两个变量没有单位根，是平稳的（但为了符号上的统一，我们也进行了一阶差分）。这样，需要考察的四个变量都变成了平稳的，因而就可以进行下一步的协整检验了。

二、VAR模型的构建

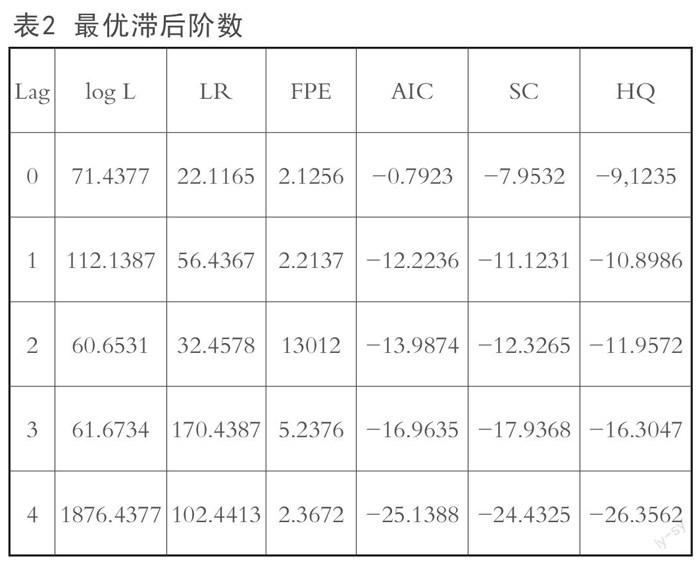
四个变量在经过单位根检验以后，结果两个平稳、两个非平稳，而经过一阶差分处理以后，四个变量均平稳。对这四个变量建立向量自回归模型，即VAR模型构建。建立VAR模型的一个重要前提就是确定一个滞后阶数，這个滞后阶数我们务必选到最优的，这是保证模型完整性的一个十分重要的逻辑基础。通常这个最优滞后阶数的选择方法有AIC准则、SC准则以及LR准则等，为了尽量做到最优，我们依次用这几种准则得出结果，再进行对比，对比结果如表2所示。根据下表的对比，本文选出了为最优滞后阶数，见表2。

三、Johansen 协整检验

四个变量在经过单位根检验以后，结果两个平稳、两个非平稳，而经过一阶差分处理以后，四个变量均平稳，并且确定了最优滞后阶数为1。下面我们在滞后阶数确定为1 的前提下对四个变量进行协整检验。检验结果见表3―5。

从上述的三个表格中可以看出，FGM、FXL、FJG与JSL之间都存在一个协整方程，也就是说存在协整关系。因此本文构建了三个协整方程来分析FGM、FXL、FJG与JSL之间的关系。

四、格兰杰因果检验

通过建立的协整方程，我们就可以了解到山东省农业科技进步分别与山东省农村金融发展规模、农村金融发展效率、农村金融结构之间的长期规律。但是为了突出JSL分别与FGM、FXL 、FJG 之间的因果关系，即一个变量的变化是否会在一年后影响到另一个变量的变化，我们对这四个变量进行滞后阶数为1的格兰杰因果检验，检验结果见表6。

通过上表的格兰杰因果检验，我们可以得出如下结论：①FGM和JSL互为因果关系，即一个地区的农村农业金融发展在一年以后会引起该省农村农业科学技术进步，而同时该地区农村农业科学技术进步，又会反过来影响其农村农业金融发展规模;②FXL不是JSL的原因，但是JSL是FXL的原因，即一个地区农村农业科学技术进步一年以后并不会引起农村农业金融规模发展的变化，但是山东省农村农业金融规模发展在一年以后会引起农业科技的进步;③FJG是JSL的原因，但JSL并不是FJG的原因，农村农业金融产业结构的变化会在一年后引起农业科技的进步，但是农村农业科学技术进步并不能在一年后影响农村农业金融产业的结构变化。[1.课题项目：本文系2021年度山东省软科学研究计划项目《农业科技金融助力山东省绿色农业高质量发展的研究 》（编号：2021RKY03054）的阶段性研究成果。2课题项目：本文系2021年度山东省社会科学普及应用研究项目《新发展阶段下，图解普惠金融下沉与农村居民幸福感提升》（编号：2021―SKZZ―116）的阶段性研究成果 。