初中几何辅助线专题——平移变换

栾长伟

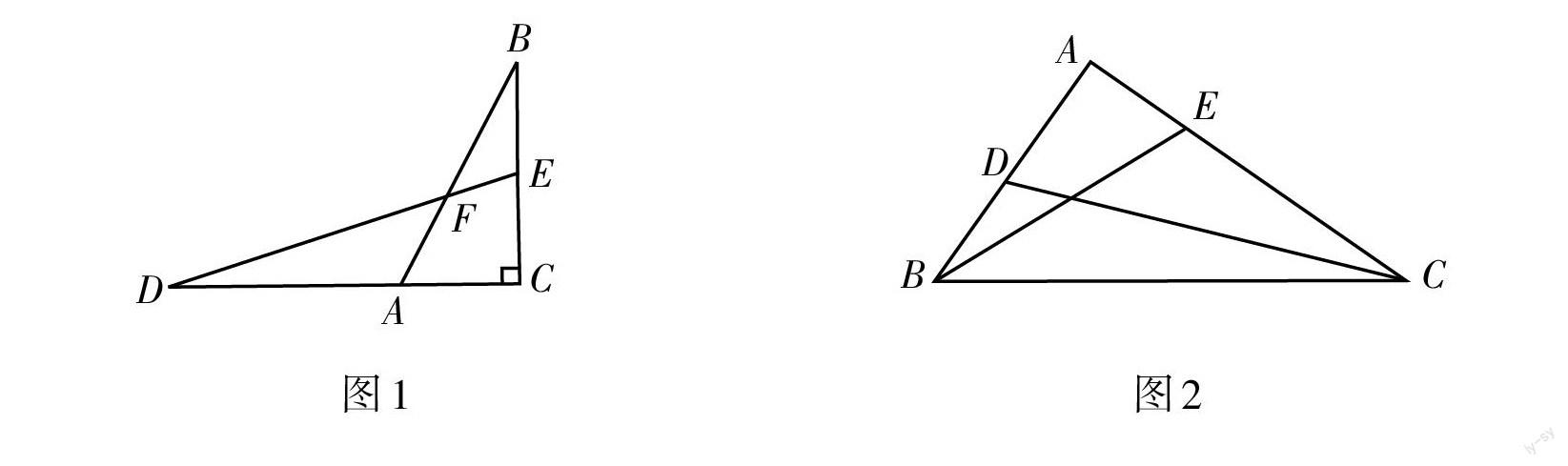
本课选自辽宁省教育厅主办、辽宁教育学院承办的“辽宁省义务教育阶段名师公益课堂”，旨在贯彻落实国家“双减”政策，帮助广大师生自主学习和个性化提升。在“学到汇”平台收看本课已达15.1萬人次。

初中数学中有三大变换：平移、翻折和旋转.每一种变换都有其固定的变换方式.平移变换的两要素为平移的方向和平移的距离;翻折变换凸显轴对称性，常见于角平分线、等腰三角形的对称性等;旋转变换强调旋转中心、旋转方向和旋转角度. 这三种变换均为全等变换.

本课研究如何通过平移变换解决一类几何试题，主要包括如下内容：

一、满足什么条件的几何问题才可以进行平移变换，即“定线段、定夹角”.

二、解释常见的“定线段、定夹角”的基本类型，如线段相等、线段已知及线段成比例等，都可以归为“定线段”;“定线段”的夹角或者“定线段”所在直线的夹角可以视为“定夹角”，这个角通常选用特殊角;在此基础上，研究满足平移变换的条件后怎样进行平移，即选择“定线段”的端点的连线作为平移的方向和距离，构造平行四边形.

三、结合具体问题，阐述如何构造辅助线转化已知条件与所求结论，从而完成平移类几何问题的解答.

典型例题：如图1，在Rt△ABC中，∠C = 90°，D在CA的延长线上，E在BC上，连接DE交AB于F，AD = BC，AC = BE，求证：∠AFD = 45°.

平行练习：如图2，在Rt△ABC中，∠A = 90°，D，E分别在AB，AC上，AE = BD，AB =CE，探究CD，BE的数量关系. （答案见第29页）

（作者单位：大连市甘井子区教师进修学校）