高中物理能量守恒在解题中的应用探究

摘 要：能量守恒是高中物理的重要知识点，是高考的熱门考点.为提高学生运用能量守恒解答物理习题能力，应注重结合具体例题做好能量守恒在解题中的应用讲解，进一步澄清学生认识，深化其对能量守恒知识的理解，牢固掌握相关的应用方法与应用技巧.

关键词：高中物理;能量守恒;解题;应用;探究

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2022）22-0107-03

高中物理中能量守恒的内容虽然较为简单，但要想深刻理解、灵活应用并非易事.为使学生正确、灵活应用能量守恒解答不同类型的物理习题，应做好相关习题类型的汇总，使学生见到更多的物理习题，尤其通过示范具体的解题过程，使其掌握破解的思路与技巧.

1 用于分析板——块相对运动问题

做功与能量的变化密切相关，是能量转化的量度.运用能量守恒分析板块相对运动问题时应注重从做功切入.一般情况下除重力或弹簧弹力之外的其他外力对物体做正功会使其机械能增加，反之会减小.解题时结合题干创设的情境，对板、块的运动状态有个整体的把握与判断.同时通过对板、块分别进行受力分析，明确其所受的力、力的方向以及对应力做功的正负.思考力做功使哪些物体的能量发生了变化，把握物体能量的来源以及去向，如此也就不难分析出正确结果.

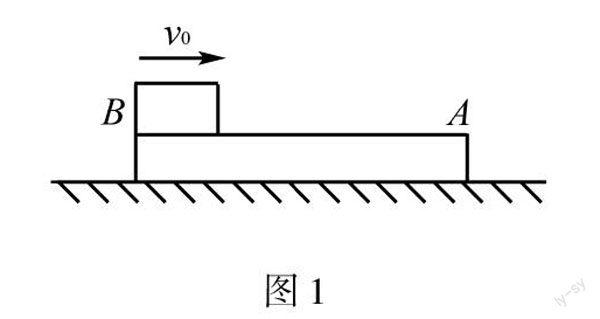
如图1所示，在光滑的水平面上放一长木板A，某时刻物块B以水平速度v0冲上A后，由于摩擦力作用最后停止在木板A上.则以下分析正确的是（）.

A.物块B动能的减少量等于系统损失的机械能

B.物块B克服摩擦力做的功等于系统内能的增加量

C.物块B损失的机械能等于木板A获得的动能与系统损失的机械能之和

D.摩擦力对物体B做的功和对木板A做的功总和等于系统内能的增加量

分析 物块B滑上木板后受到摩擦力的作用做匀减速运动，摩擦力对其做负功.木板A受到摩擦力的作用做匀加速运动，摩擦力对其做正功.两者速度达到一致，不再发生相对滑动.需要注意的是木板A的速度未和物块B的速度达到一致时，会因木板A和物块B之间的相对滑动而产生热量.由能量守恒可知，木块B因受到摩擦力动能减小，减小的动能一部分转化为A的动能，一部分因摩擦转化为内能，因此，只有C项正确.

2 用于分析弹簧

——斜面问题运用能量守恒分析弹簧-斜面问题时应把握两点：（1）弹簧受力发生形变，其他形式的能转化为弹簧的弹性势能，并在弹簧中储存起来.当弹簧恢复到原长的过程中也就是能量释放的过程，当弹簧达到原长时，储存的能量完全释放.（2）在斜面上运动的物体与弹簧发生作用时，其速度达到最大的点是物体受力平衡的点，此时弹簧处于压缩状态.

如图2所示，将质量为1kg的滑块放在倾角为30°的光滑斜面的a点，由静止下滑，b点开始压缩弹簧，c点时达到最大速度，d点（图中未画出）时开始弹回，刚好能够再次回到a点，若bc=0.1m，弹簧弹性势能的最大值为8J，g取10m/s2，则（）.

A.弹簧的劲度系数为50N/m

B.d→b点，滑块克服重力做功8J

C.滑块的动能最大值为8J

D.d→c点，弹簧的弹力对滑块做功8J

分析 滑块在c点速度达到最大，表明其受力平衡，由平衡条件以及胡克定律可得mgsin30°=kx，x=bc，解得x=50N/m;d→b点由机械能守恒可知，弹簧弹性势能转化为滑块的重力势能和动能，克服重力做的功仅是重力势能的增加量，因此，滑块克服重力做功应小于8J;弹簧弹性势能的最大值为8J，该能量全部由滑块从a→d点时减少的重力势能转化而来，滑块只要离开d点均有部分能量转化为动能，因此，滑块的最大动能不可能达到8J;弹簧只有在b点原长时，才会将所有的弹性势能转化为滑块的机械能，因此，d→c点，弹簧的弹力对滑块做功达不到8J.综上只有A项正确.

3 用于计算物块——斜面问题

运用能量守恒计算物块-斜面问题时应明确不同形式能量的计算表达式，注重思考表达式中一些参数与其他知识点之间的关联，如动能计算式中含有速度“v”，能和平抛运动、圆周运动以及动量定理、动量守恒定律相关联.同时，运用其他知识计算速度“v”时应注重相关定理、定理成立的条件，避免张冠李戴，生搬硬套.如在某一方向上系统不受力或所受的合外力为零时可运用动量守恒定律求解速度“v”.

如图3所示，一光滑水平面上有一倾角为θ，高为h的光滑斜面M.某时刻一小物块以一定的初速度沿水平面向右运动.忽略小物块冲上斜面时的机械能损失.已知斜面的质量是小物块质量的2倍.当斜面固定时小物块恰好能冲到斜面顶端.若斜面不固定，则小物块冲上斜面后的最大高度为（）.

分析 当斜面固定时小物块的机械能守恒，即12mv2=mgh.当斜面不固定时，系统在水平方向上动量守恒.设其共同速度为v′，小物块上升的最大高度为h′，则由动量守恒定律可得：mv=3mv′.整个过程由机械能守恒得到：12mv2=mgh′+12（m+2m）v′2，整理解得h′=2h/3，选择C项.

4 用于解答物块——圆弧问题高中物理综合性问题涉及的物体运动过程较为复杂，对学生综合分析问题的能力要求较高.运用动量守恒解答该类问题应注重把握两点：其一，思考分析物体参加了哪些形式的运动，是圆周运动还是平抛运动以及这些运动遵循哪些规律.其二，通过认真审题，把握物体运动的全过程，掌握能量的来源与去向，既可从整体角度构建能量守恒方程，也可对物体的运动过程进行拆分，构建对应运动过程的能量守恒方程，具体应根据题目设计的问题来定.

如图4所示，一半径R=0.4m的光滑圆弧BC固定在竖直平面内.轨道最高点B和圆心O的连线和水平方向的夹角θ=30°，最低点C和粗糙水平面相切.在水平面上有一右端固定的轻质弹簧.一质量m=0.1kg可视为质点的小物块，从空中A点以v0=2m/s水平抛出，刚好从B点进入轨道，经C点沿水平面向右运动至D点，弹簧被压缩至最短. C、D两点间的水平距离L=1.2m，小物块和水平面间的动摩擦因素μ=0.5，g取10m/s2，求：

（1）小物块经过圆弧轨道上B点时速度vB的大小;

（2）小物块经过圆弧轨道上C点时对轨道的压力大小;

（3）弹簧的弹性势能的最大值Ep;

分析 对于问题（1）因小物块A刚好从B点进入轨道，表明其进入轨道时和圆弧的半径垂直，则由几何关系可得v0vB=sinθ，代入数据解得vB=4m/s.问题（2）从B→C点，设小物块在C点的速度为vC，经过圆弧轨道上C点时对轨道的压力为N，由机械能守恒可得：12mv2B+mgR（1+sinθ）=12mv2C，由圆周运动规律可得：F-mg=mv2CR，由牛顿第三定律得到F=N，代入数据解得N=8N;问题（3）从C→D由能量守恒可得：12mv2C=μmgL+Ep，解得Ep=0.8J.

5 用于解答碰撞问题教学实践中为提高学习者解答该类问题的能力，一方面，为学习者透彻地讲解相关理论知识，尤其结合具体案例与其一起推导物理方法，使其深入理解，牢固掌握.另一方面，为使其掌握相关解题思路，应注重结合多媒体技术为其展示物体碰撞的具体情境，把握碰撞前后物体运动特点，以更好地找到解题切入点，增强其解题自信心.同时，要求学习者做好解题反思，及时发现与堵住知识漏洞.

将一质量为m和14m的A、B两个小球通过弹簧连接，放置在光滑水平面上，如图3所示，静止时弹簧处于原长.小球B的右侧有一竖直挡板（未画出）.给求A一个瞬时冲量，其获得速度v0.当小球和挡板正碰后立即将挡板撤走，忽略碰撞过程中的机械能损失，则B和挡板碰后运动过程中弹簧弹性势能的最大值可能为（）.

分析 该题较为抽象，解题的关键在于吃透题意，确定B球和挡板在何种情况下两球共速的速度最大或最小.由机械能守恒可知，弹簧最大弹性势能必然小于12mv20，且最大值一定是两球共速的時候.设共速的速度大小为v，由能量守恒可得Ep=12mv20-12（m+14m）v2.B和挡板碰后由动量守恒定律可得：mv1-14mv2=（m+14m）v.当弹簧第一次恢复原长时B和挡板相碰，由mv0=mv1+14mv2，12mv20=12mv21+12·14mv22，解得v1=35v0，v2=85v0，碰后只是速度方向发生改变，因此，mv1-14mv2=15mv0;当B的速度很小接近为零时和挡板相碰，v1=v0，v2=0，碰后由mv1-14mv2=mv0，由上可得425v06 用于解答电磁感应问题

教学实践中一方面与学习者一起分析电磁感应中的能量转化方向以及转化路径，帮助学习者构建清晰、系统的知识体系，为运用能量守恒解决问题做好铺垫.另一方面，为防止学习者在解题的过程中走弯路，课堂上应围绕具体问题与学习者积极交流，帮助其更好的找到解题的切入点.同时，注重给学习者预留空白时间，要求其尝试着写出解答过程，进一步加深其印象.

如图4所示，将MN与PQ两根电阻不计的导轨相距为L，平行固定在水平面上.其中弯曲部分不计阻力，水平部分有阻力.右端和一阻值为R的定值电阻相连.磁感应大小为B的匀强磁场，方向垂直导轨水平部分竖直向上.由静止将一电阻为R，质量为m的金属棒由图中释放，在水平导轨上运动的距离为d时刚好停止.金属棒和导轨水平部分的动摩擦因数为μ，重力加速度为g.求金属棒产生的焦耳热以及金属棒在磁场中运动的时间t.

分析 该题创设的情境并不复杂，解题的关键在于具备整体意识，列出能量守恒方程.同时，注重运用电磁感应以及电学知识，明确能量在电路中各对象上的分配情况.金属棒由静止释放，在水平面上运动d距离，由机械能守恒可得，Q=mgh-μmgd，因金属棒和定值电阻的阻值相等，因此，金属棒产生的焦耳热为12mg（h-μd）;金属棒由静止下滑，由机械能守恒得到：mgh=12mv20，金属棒通过磁场产生的电荷量q=ΔΦ2R=BLd2R，整个过程由动量定理得到：-BI-Lt-μmgt=0-mv0，而q=

I-t，将以上各式联立解得t=2ghμg-B2L2d2Rμmg.

能量守恒定律是自然科学中最基本的定律之一，在分析物理问题中有着广泛的应用.高中物理教学中为提高学生运用能量守恒解答相关习题的能力，应在深入讲解能量守恒理论知识的基础上为学生展示能量守恒在不同问题情境中的应用，使学生更好的把握能量守恒本质，掌握相关的应用思路与技巧.

参考文献：

[1]马彦平.能量守恒在解决高中物理问题方面的应用探讨[J].课程教育研究，2020（05）：182.

[2] 杨黎明.高中物理高考中能量守恒定律的综合应用[J].高考，2019（35）：128.

[责任编辑：李 璟]

收稿日期：2022-05-05

作者简介：宋晨光（1993.2-），男，山东省滨州人，本科，中学二级教师，从事高中物理教学研究.