指向数据分析能力培养的教学实践与探索

王璨

[摘  要] 以“复式折线统计图”为例，尝试进行指向数据分析能力培养的教学实践与探索，以培养学生数据分析能力为核心，使学生意识到利用统计的方式解决问题的独特优势，并引导学生通過对数据的对比和分析，预测数据的未来发展趋势，从而把学生的数据分析能力提升到一个新的层次。

[关键词] 数据分析;教学实践;教学探索;复式拆线统计图

伴随着科学信息的快速发展，人类社会逐渐进入“大数据”时代，人们越来越多地面临烦冗复杂的数据信息，如何从这些海量的数据信息中发现数据本身的规律，提取对自身有用的信息呢？培养学生的数据分析核心素养就显得至关重要。因此，在小学数学的教学中，教师要引导学生在解决问题的过程中，通过收集数据、整理数据、分析数据和描述数据等环节，揭示某一事物的发展规律和未来趋势，并在此过程中，培养学生的数据分析能力。笔者以“复式折线统计图”为例，尝试进行指向数据分析能力培养的教学实践与探索，期望为广大教育同人提供有价值的借鉴和思考。

[?]一、创设情境，引出复式图

“好的开端是成功的一半。”在新授课中，教师不必急于切入主题，可结合小学生身心发展特点和认知规律，创设生动的情境，把学生的思维逐步导入新课的学习中。关于新课导入，教师可从以下两个方面把握：一是从现实生活入手。小学生对知识的认知往往源于现实生活中的具体事物和实例，教师以现实生活中的事物切入主题，往往就能吸引学生的注意力。二是把握新知识与旧知识的联系，引发思维冲突。数学新知识与旧知识之间往往存在着比较密切的联系，教师可以从新旧知识连接点入手，使学生运用旧知识解决问题时产生困惑和迷茫，使之处于“思之而不得”的心境中，由此产生对学习新知识的强烈渴望。

师：同学们，现在大家已经上六年级了，你们的身高各是多少呢？

生1：我的身高是150厘米。

生2：我的身高是153厘米。

生3：我的身高是154厘米。

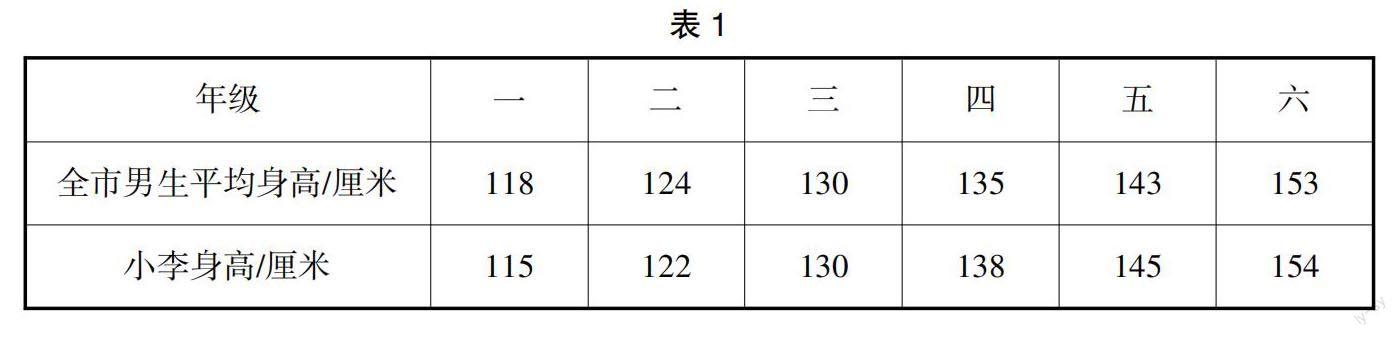
师：从一年级到六年级，同学们的身高都发生了很大的改变。那么，你的身高与全市学生的平均身高相比，是更高些还是更低些呢？表1是小李同学收集到的数据表。

师：同学们观察这些数据，说一说小李在几年级的时候与全市男生平均身高的差距最大。

生4：我们需要先把小李身高与全市男生平均身高之差算出来，然后比较大小。具体为：一年级是118-115=3（厘米），二年级124-122=2（厘米），三年级是130-130=0（厘米），四年级是138-135=3（厘米），五年级是145-143=2（厘米），六年级是154-153=1（厘米）。所以，在一年级和四年级时小李身高与全市男生平均身高的差距最大。

生5：这个办法计算起来比较麻烦，而且也不直观。如果能把这些数据都画在图上再进行比较，就方便多了。

生6：我们已经学过折线图的画法。我可以把小李身高和全市男生平均身高分别画在折线图上，这样就能比较了。

生5：这样也不好。两条折线不在同一个图上，比较起来还是比较麻烦。

师：那我们能不能把两条折线画在同一个图上形成一个复式统计图呢？

（学生议论）

师：心动不如行动。我们还是动手尝试一下吧！

教学中，教师引导学生运用前面学习的单式折线图解决现实问题，结果学生发现仅凭单式折线图并不能很好地比较小李身高与全市男生平均身高，这就引起了学生的思维冲突，使学生产生了学习新知识解决问题的欲望。

[?]二、整理数据，绘制统计图

绘制统计图是学生学好数学的一项重要能力，也是培养学生数据整理和数据分析能力的重要途径。课堂教学中，教师要充分调动学生的积极性，引导学生亲自动手绘制统计图，把表格中的数据转化到生动直观的统计图中，使学生初步体验统计图的直观优势。在这个过程中，需要注意的是，一要引导学生整理数据。正确地整理、分析数据是绘制统计图的基础。在绘制复式折线图的过程中，对于纵轴的数据分段是提升学生整理、分析数据的关键环节。二要注重绘制细节。在绘制过程中，教师要引导学生把数据准确地体现在图上，要求学生注意作图的规范性，最大限度地减少绘制过程中的误差，这样不但能培养学生细致严谨的数学精神，还可以为下一步的数据比较和预测打下基础。

师：在画图之前，我们先要明确，用横轴代表什么项目，用纵轴代表什么项目？

生7：可以用横轴代表年级，可以用纵轴代表身高。

师：那么，应该把身高分为几段呢？

生7：最低的身高是115厘米，最高的身高是154厘米。所以可以把110厘米作为纵轴上除0以外的第一个数据;（154-110）÷5≈10（厘米），所以用1个大格代表10厘米，也就是把身高的数据分为5个段，分别是110—120、120—130、130—140、140—150、150—160（单位：厘米）。

师：确立了横轴和纵轴代表的项目，又确定了纵轴上的单位长度，那么，还有一个问题需要解决，如何区分开两条折线呢？

生7：可以用两种不同颜色的线，这样就能区分开了。

师：如果只有一种颜色的笔呢？

生8：那我们可以用实线和虚线分别代表不同的数据。

师：明确了这些问题，我们现在可以开始画图了。

（学生画图，教师巡回指导）

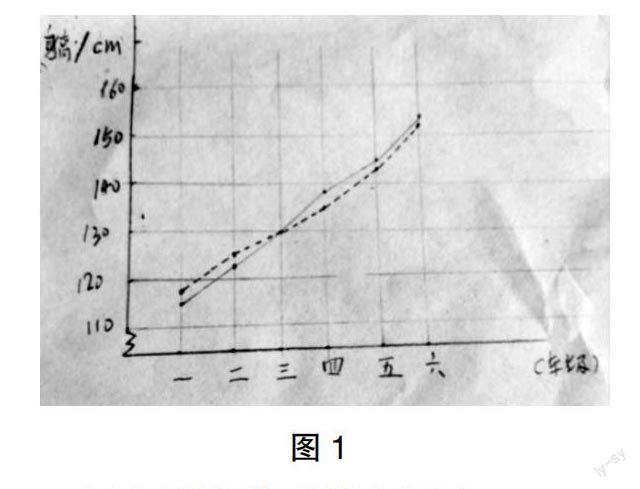
生7：这是我画的图（图1）。我先确定纵轴上的单位长度，用1个大格（1厘米）代表10厘米，然后在统计图上按照数据描出各个点，再分别用虚线和实线把各个点连接起来。

师：同学们能看懂这幅图吗？

生8：虚线代表什么，实线又代表什么呢？

生7：虚线代表全市男生的平均身高，实线代表小李的身高。

师：每个人看自己的图，都能明白每条线代表谁的数据。可是，统计图是用来交流的，在很多时候是给别人看的，我们怎么样能让别人一眼就看懂我们画的图呢？

生7：我們可以在图上标出来每条线代表谁的数据。

师：对，这就是图例。图例要写在统计图的右上角。

（生7在统计图上加上图例）

师：如果我把这幅加上图例的统计图拿给别人看，别人能看得懂吗？

生9：别人可能会有这样的疑问：这幅统计图描述了什么事情？

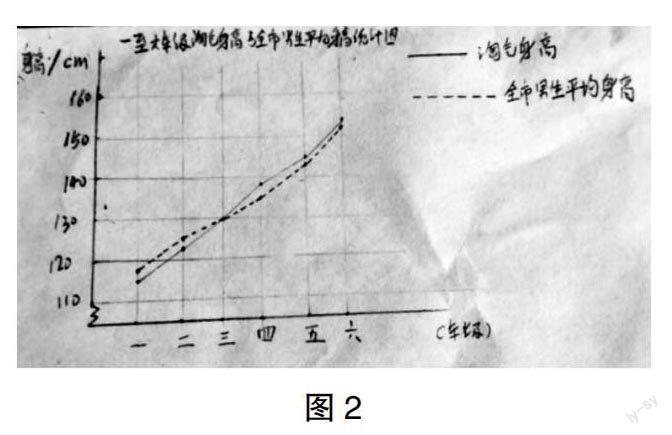
师：所以，我们还要给这幅统计图起个名字，在统计图上方注上标题。

生7：这样就比较完整了。

师：同学们，这就是复式折线统计图。大家把它和以前我们学过的单式折线统计图对比一下，看看它们有什么区别。

生7：单式折线统计图有一条线，而复式折线统计图有两条线。

生8：单式折线统计图只能直观地看出一个事物的发展变化情况，而复式折线统计图能够看出两个事物的发展变化情况。

生9：通过复式折线统计图可以容易地比较两组数据，并体现数据的变化趋势。

教学中，绘制复式统计图既是一个学生运用绘图工具作图的操作过程，同时也是一个学生整理数据、分析数据的过程。首先，教师引导学生通过观察、计算数据，确定在纵轴上用1个大格代表10厘米，培养学生的数据整理和分析能力;其次，教师通过“加图例”“写标题”等环节，使学生绘制的复式折线统计图逐渐完善，并在这个过程中培养学生严谨认真的治学精神;最后，通过对比单式折线统计图和复式折线统计图，既沟通了新旧知识的联系，又使学生初步体验了复式折线统计图的优势。

[?]三、多层次分析，解读统计图

数据分析能力是信息社会对公民提出的重要要求。数据分析能力是建立在学生数据搜集、数据整理、数据分析和数据描述的基础上逐渐形成的。要提升学生的数据分析能力，最有效的办法就是让学生真正经历数据分析的过程。学生从统计图表中获得信息，并依据这些信息进行分析、判断，最后对事物未来的发展方向做出预测。教师要引导学生对数据做出多层次分析，逐渐激活学生的数据分析观念，提升学生的数据分析能力。

师：从统计图上看，小李身高在几年级时与全市男生平均身高相差最大？在几年级时二者相差最小？

生10：从图上看，在一年级和四年级时，小李身高与全市男生平均身高的差距最大，在三年级时二者的差距最小。

师：你是怎样看出来的？

生10：两条折线之间的距离越大，说明两组数据的差距越大;两条折线之间的距离越小，说明两组数据的差距越小。

生11：复式折线统计图让数据的比较变得更加直观了，也更加简单了。

师：小李身高在哪个阶段增长得最快？

生12：小李身高在五年级到六年级这个阶段增长得最快。

师：你是怎样看出来的？

生12：在这个阶段折线最“陡”，说明这个阶段的数据变化幅度最大。

师：小李身高在全市男生中所占的位置有变化吗？

生13：有变化。从统计图上看，小李身高在一、二年级时低于全市男生平均身高，在三年级时与全市男生平均身高相同，在四年级至六年级时高于全市男生平均身高。

师：据统计，全市九年级男生的平均身高是164厘米，请你预测一下三年后小李在九年级时的身高是多少。

生14：在三年内，全市男生平均身高可能增长164-153=11（厘米），所以按照这样估算，小李在三年后九年级时的身高可能也会增长11厘米，为154+11=165（厘米）。

师：复式折线统计图不但能够表示两组数据的多少和增减变化，还能够预测数据的发展趋势。

读懂统计图，从统计图中提取有效信息，是培养学生数据分析能力的重要举措。教学中，教师引导学生对复式折线统计图展开多层次的数据分析和描述，不但凸显了复式折线统计图的独特优势，还培养了学生通过解读统计图分析数据信息的能力;此外，教师引导学生以动态的观点观察、分析数据的变化规律，预测三年后小李的身高，提升了学生数据分析的深度，使学生的统计思维变得更加深刻而灵活。

统计知识的教学不能把主要精力聚焦于某个知识点，而应该致力于培养学生的数据统计意识和数据分析能力，使学生切身体会到数据统计在认识外部世界中起到的重要作用。因此，教师在教学中应该以培养学生数据分析能力为核心，通过画图、读图等环节，使学生意识到利用统计的方式解决问题的独特优势，并引导学生通过对数据的对比和分析，预测数据的未来发展趋势，把学生的数据分析能力提升到一个新的层次。