运用直观性教学策略,促进学生数学思维发展
苏茸花

[摘 要] 新课改风向标下,教师需认清小学生的思维特征,恰当地运用直观性教学,让学生更好地理解数学知识,获得思维能力的自然提升。文章结合具体教学实践,提出促进学生思维发展的直观性教学策略:基于学科特征的直观方式唤醒思维,基于学生认知规律的直观方式发展思维。
[关键词] 直观性教学;小学数学;数学思维
直观性教学策略就是在教学过程中,通过实物、模型及语言等刺激,伴随着对学生思维的唤醒、指引和发展,让学生经历观察、实验、探究、讨论等过程,最终创造性地实现从具体思维到抽象思维的顺利过渡。小学生的思维特征是形象思维占据优势,并逐步向着抽象思维过渡,教师要认清小学生的这一思维特征,恰当地运用直观性教学,让学生更好地理解数学知识,获得思维能力的自然提升。
[?]一、基于学科特征的直观方式唤醒思维
数学学科本身是一个奇妙的混合体,抽象与直观、特例与一般性结论等的共存,无一不彰显着学科本身的魅力。因此,我们在赞叹数学知识的抽象性的同时,也需要接受抽象这座令学生难以逾越的陡峭山峰。同样的,对于小学生而言,思维是何物,它的价值是什么,并非借助语言就可以理解的。因此,在教学的过程中,我们需要借助直观方式,沿着直觉的方向进行教学,以唤醒学生的思维,让学生在自主自发的感知中体验思维、生长思维。
案例1 以“认识钟表”的教学为例
师:大家看,这样拨动钟表,你们发现了什么?(实物演示:拨动分针从12时到1时)
生1:当分针行走1圈时,时针走了1大格。
师:这样呢?(继续拨动分针到1时1分)
生2:分针行走了1小格,时针没有变化。(其余学生也都点头表示赞同生2的观点)
师:从12时到1时分针与时针都有不同程度的行走,而再到1時1分却只有分针行走了,这是为什么呢?
生3:我觉得是因为1小时时间比较长,而1分钟时间比较短。
师:那我们再来试一试。(教师再一次进行了演示,显然肉眼的确无法观察到时针在动)
师:那从1时1分到1时2分,分针再走1分钟,时针动了吗?
生4:时间还是太短,没有动。
师:那依照你们的想法,从1时开始,我们每次只拨动1分钟,由于时间过短,只有分针动时针不动。如此这般拨动60次,分针行走完1圈,此时是2时,那时针应该还在原地,对吗?(学生开始面露难色,显然这有悖于他们的已有认知经验)
师(拾级而上):事实上,分针每行走1小格,时针也在行走,只是由于行走的速度太慢,我们肉眼无法看出来。
生5:我们如果用放大镜应该就能看出来了。
师:嗯,这个方法的确值得一试。这样就可以解释60分钟后,时针从“1”行走到了“2”(教师再一次完成实物演示)。可见,逻辑分析问题是一项很重要的本领,有时候除去用眼睛观察和发现,我们还应学会逻辑分析……
小学生都是充满好奇和想象力的个体,他们喜爱探究,却时常会凭着直觉给出观点,这里就需要教师为学生的思考树立榜样,通过学生喜爱的方式唤醒学生的思维。当然,其中的道理学生未必能完全知晓,大部分学生仅仅是有了一个模糊的印象,而此处教师的意图也仅仅是给学生初步感知思维价值的机会,让学生在欣赏思维之美的同时,唤醒思维意识,这样一来,才能为思维的发展谋求出路。
[?]二、基于学生认知规律的直观方式发展思维
美国哲学家、心理学家杜威提出“做中学”“活动中学”“经验中学”。从杜威的教育理念中,我们可以清楚地发现直观性教学的重要意义。作为教师,我们只有基于学生的认知规律,通过生动活泼的直观方式去融化冰冷的抽象,才能促进学生思维的发展,进而让学生的思维真正意义上走向深入。
1. 实物直观教学
教师常常会发现,很多刚入学的一年级学生喜欢通过扳手指进行加减计算,但有些教师认为计算时只有脱口而出才是计算能力拔节的表现,所以不允许学生采用扳手指这种直观方法。而在这种强压下,大部分学生不仅计算能力没有提升,反而对计算产生了厌倦情绪。
教育心理学表明,认知往往源于感知。倘若在计算3+5=8时,给予学生扳手指的权利,那学生定然可以通过操作过程感知8的意义,从而自然接受这个答案;相反地,倘若让学生死记硬背掌握了3+5=8,那是否能真正理解就不得而知了。所以,扳手指这种直观操作行为可以帮助学生找寻到强有力的思维支撑,以促进表象的构造,从而为后期的“脱口而出”提供助力。
2. 语言直观教学
语言直观就是通过生动且富有感染力的语言让学生的脑海中重现相关事物的表象,且在语言外壳的渲染下重组,进而形成新的表象,自然进行抽象的思维,以获得对新知的领悟和掌握。
案例2 红红妈妈做了54个小面包,红红带走了22个,红红弟弟带走了8个,还剩下多少个?
师:大家先仔细读题,之后说一说你准备先求什么,再求什么。(学生沉思片刻后生成了各种各样的求解思路,跃跃欲试)
生6:我是先求红红带走22个后剩了多少个,再求红红弟弟带走8个后剩下了多少。
生7:我是先求红红弟弟带走8个后剩了多少个,再求红红带走22个后剩下了多少。
生8:我是先求红红和红红弟弟一共带走了多少个,再求剩下了多少个。
师:哇,你们都是善于思考的好孩子,居然有这么多解决问题的思路……
正是因为有了教师语言直观的指引,才让学生的数学思考和交流有了方向,才让学生的数学思维源源不断地流淌,促进了语言表达能力和有序思维能力的形成,这不正是素质教育想要的效果吗?
3. 变通直观教学
数学问题往往是千变万化的,面对不断变化的难题不少学生常常一筹莫展。这就需要教师通过直观与变通相结合的教学方式去启发诱导,当学生理解不了抽象事物时,变通角度去调动学生的表象思维,化抽象为具象,为学生的数学思考找到入手点。
案例3 以一道发散思维的习题教学为例
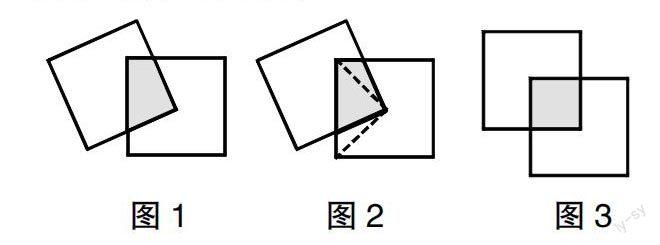
问题:图1是两个大小相同的正方形(边长为2厘米),且一个正方形的顶点刚好落于另一正方形的中心,试求出阴影部分的面积。
分析:本题难度较大,不少学生思维卡壳,根源在于学生面对这个不规则阴影部分难以下手。他们往往采用一般性思路,如作出图2所示的辅助线,而这里阴影部分的面积一定与三角形面积相等吗?这一点学生仍然无法确定,使其陷入解题困境。为了更好地给学生释疑解惑,笔者选择采用变通直观教学让学生去感知、去思考、去领悟。
师:我们像图3一样将斜着的正方形转正,现在阴影部分的面积你会求吗?
生9:这也太简单了吧!阴影部分面积不就是正方形面积的1/4吗?
师:那图1和图3有何异同点?
生10:不就是把斜着的正方形放正了吗?其他应该没有不同的吧。
师:不错,两幅图的生成方式和图形结构都相同,那么图1和图3必定存在内在规律。你们觉得图1的阴影部分面积也刚好是正方形面积的1/4吗?(学生又一次陷入沉思,有些开始小声讨论,有的开始涂涂画画)
生11:我觉得是的。(其他学生也点头表示赞同)
师:既然你们有了这样的猜想,那就让我们一起来验证一下是否正确。(用PPT出示图4)
生4:哇,真的是1/4!只是被平均分成了四个“斜”的阴影四边形。
直观思维是对事物本质的直接洞察,可以直达问题的本质。本题的知识起点是“掌握正方形面积的求法”,因此,在解决本题时学生的思维表现大多相同,不管是三年级的学生,还是六年级的学生,一旦学会通过直观与变通相结合的方法进行思考,都能快速地释疑解惑。反之,如果无法自然运用直观方法,又或是在解题的过程中思维不会变通,那定然一筹莫展。这里正是有了直观思维的参与和变通思维的指引,才让问题的解决简洁而流畅,而这对发现规律、做出判断和探寻解决问题的思路都有好处。
总之,生动直观是抽象思维的关键所在,尤其是对于以直观思维为主的小学生而言,直观教学可以唤醒他们的思维,让他们的数学思维获得长足发展。因此,教师在教学过程中需要恰当地应用好直观教学法,在为学生的数学学习和探究带来乐趣之余,增進学生的求知欲望,启迪学生的创造性思维,这才是新课程改革下的数学课堂教学所要追求的。

