推理教学的实践与反思

周艳

［摘 要］推理是学生数学学习的重要方式，培养合情推理能力和演绎推理能力是发展学生数学学科核心素养的重要举措。在小学数学教学中，教师应想方设法给学生创设更多的推理空间，让学生充分经历数学推理的过程，积累丰富的推理经验。

［关键词］推理；经验；规律

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2022）29-0033-03

推理是学生数学学习的重要方式，培养合情推理能力和演绎推理能力是发展学生数学学科核心素养的重要举措，也是数学学科的主要教学目标。那么，教师怎么才能给学生创设更多的推理空间，让学生充分经历数学推理的过程，积累丰富的推理经验呢？笔者以人教版教材二年级下册“推理”为例，通过两次教学对比得出相应的教学策略。

一、在抽丝剥茧中突出核心经验

【第一次教学】教师先用课件出示教材原图（如图1），让学生阅读图中的题目，但不用解题；接着将教材原图提炼、简化成图2，由简单的图形入手开展教学。

师：细看方格图，你有什么有趣的发现？

（师生交流互动后，呈现填数规则：方格中的各行各列只能填入1～3中的任意一个数字，并且每个数字在所在行列中不能重复出现）

师：根据目前已经掌握的条件，你能推理出A是什么数吗？说说你的思路。

师（小结）：先看第一行，只有数字1和3，可知中间空格唯一可填数字2；再看第三列，已经填入数字2和3，推知中间空格唯一可填数字1；最后看A所处的中间行和中间列，已经出现数字1和2，为了确保不重复，A处只能填数字3。

【第二次教学】教师给出三个未填入数字的九宫格（如图3-1至图3-3），然后告知学生填数规则：方格中的任意一行一列只能从1～3中任选一个数字填入，而且任何一行（列）不能出现重复数字。

师（针对图3-1）：如果此处填入1（如图4-1），其所在的行和列还能出现另一个数字1吗？如果在右上角试填3（如图4-1），此时哪个方格里的数可以确定？如果在图3-1的右下角补填2（如图4-1），此时哪个方格里的数可以确定？

师（针对图3-2）：假若在这两个方格内分别填入数字1和3（如图4-2），你认为哪个方格里的数可以确定？请指明，并陈述理由。除了左上角这一处，还有别的地方吗？（学生指出标“*”号的方格，并将此处的数字确定为2）

师（针对图3-3）：如果在这两处填入数字2和3（如图4-3），你认为哪个空格里的数可以确定？请指明，并陈述你的思路。（学生指出标“*”号的方格都应填1）

师（及时点拨）：在图3-1中，单看某一列或者某一行就成，但是在图3-2和图3-3中，这一方法就行不通了，此时需要综合所在的行和列来看。（板书：横看+竖看）

【对比性反思】此课的教学难点不在于“推理”，而是“定数”，即同时兼顾交叉行和列，这种能力是学生所缺少的。第一次教学时，教师让学生先判定首行和末列中间数字为2和1，然后综合考虑交叉行列填数情况，借此判断出A处的数字为3。把综合考虑行和列的经验混杂在单看行和列的操作中，很少有学生能同时综合行和列的信息去分析研判，整节课的教学效率低下。而第二次教学中，教师将综合统筹行和列的情况单独分离出来，一步步引导学生，使学生从中积累了经验，为学生自主总结规律、掌握方法提供了帮助。

二、在经历过程中自主发现规律

【第一次教学】教师课件出示教材原题（如图5），并给出填数规则：从1～4中任选一个数字填入，任意一行一列不能出现重复数字。

师：B处应该填几？

师（课件播放语音提示）：请先观察哪一行或者哪一列出现了三个不同的数，这样就能确定空格填几。

师：请根据提示，试着判断B处该填几。

师（小结）：看来，无法只用一步就判断出B处填几，需要知道A处填几才能确定B处填几。A所在的行和列已然出现三个不重复的数字3，2，1，那么A处的数字就只能是4，综合B处的行和列信息，得出B处只能填1。

师：你能填出其他方格里的数吗？

【第二次教学】教师改编教材原图，隐去A和B（如图6），并陈述填数规则：从1～4中任选一个数字填入，任意一行一列不能出现重复数字。

师：方格增多，情况更复杂，你认为首先可以确定哪个位置的数？请上台指认。（学生指认，教师标*号）

师：此处的数是否可以确定？请在作业纸上自己推演。

（学生自主判断，集体交流）

生₁：此处的数可能是1，2，3，4中任意一个，但是统筹考虑所在行和列后逐一排除……

师：有没有不同的推理方法？

师：看来，此处的数无法确定，我们继续观察。请在作业纸上试一试。

（学生重复上述操作）

师：很遗憾，这次也扑空了，两次都失败了，这下该如何是好？

（学生改变思路，继续寻找）

师：显然，这个位置不是随意定的。如何找准这个位置？（学生指认，教师标记）

师：那这个位置到底能不能找到？请在作业纸上试一试。

（学生自主尝试，集体交流）

师：这次找对位置了，*号处的数字可以被唯一确定为4（如图7）。

师：现在多了一条线索，下一步该确定哪个位置的数？

生₂：第二行第三列应填1。

师：你是怎么推断的？（學生阐述推断过程）

师：现在多了4和1两个数字，下一步呢？（学生填写剩余空格）

（学生集体交流，得出第二列第二行应填3，接下来学生一步步填写所有数字）

师：你能总结出解题的规律吗？

生₃：只要交叉行列一共出现3个不同数字，这个空格的数就可确定。（如图8）

【对比性反思】真正的推理必须先依赖已知，然后根据规则推出一定量的未知，最后将一定量的未知纳入已知范畴，继续根据相同规则进行推理，一步步抽丝剥茧。在第一次教学中，教师在提问“B处应该填几”后播放语音提示，学生在教材原图中位置A和语音的双重提示下率先确定了A处填几，再判断B处填几，这使得观察、猜测、操作、验证等必要的推理结构被破坏，反复猜测、验证、感悟的过程更是荡然无存。这样只是说理而不是推理。在第二次教学中，教师重点指导学生观察，让学生大胆猜测首次确定的数，学生在出现两次失误后仍能沉着冷静地调整方向，重新定位，多次总结经验教训，不断调整和完善推理思路，终获成功，最后归纳出“只要交叉行列一共出现3个不同数字，这个空格的数就可以确定”这一规律。

三、在内化方法中提升推理能力

【第一次教学】教师出示教材原图（如图9）。

师：根据填数规则，你能推断出B处应填几吗？

（学生尝试，教师巡查）

师：有同学觉得B处应填3，对吗？不过他没有陈述推理过程，关键是要提前知道谁？A是几？

师：仅仅知道A还不够，B所在的行和列的其他数字还是不能全部揭晓。如何一步步推出B是3？

师：我们在推理时，必须先找到某处所在行和列一共出现3个不同数字，这是基础，接下来再一步步确定后面的数字。

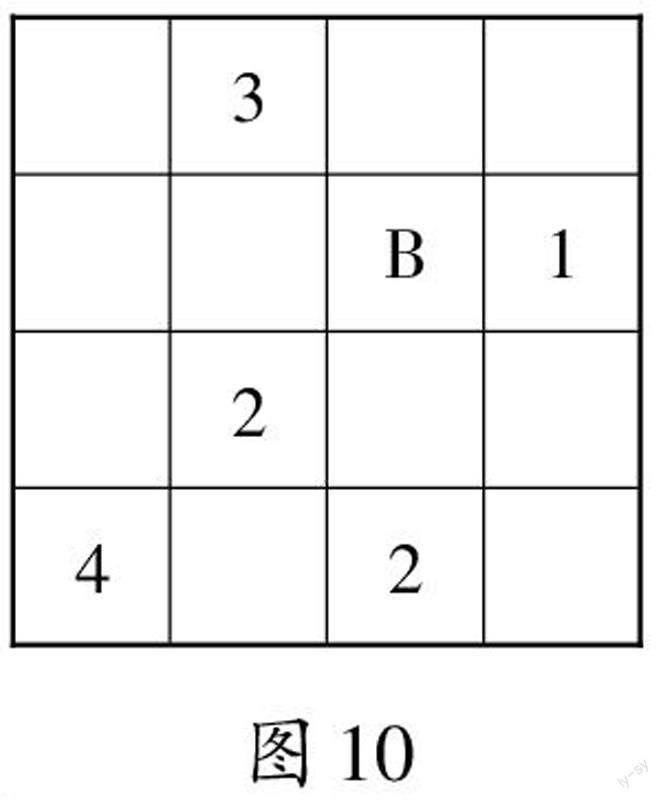
【第二次教学】教师改编教材原图（如图10），隐去字母A。

师：请看图（如图10），B处的数能直接确定吗？

生₁：不能。

师：那该怎么处理？

生₂：看B附近的数能否先确定。

师：请推测哪个位置的数是确定B的前提条件。

（学生集体交流，教师巡视）

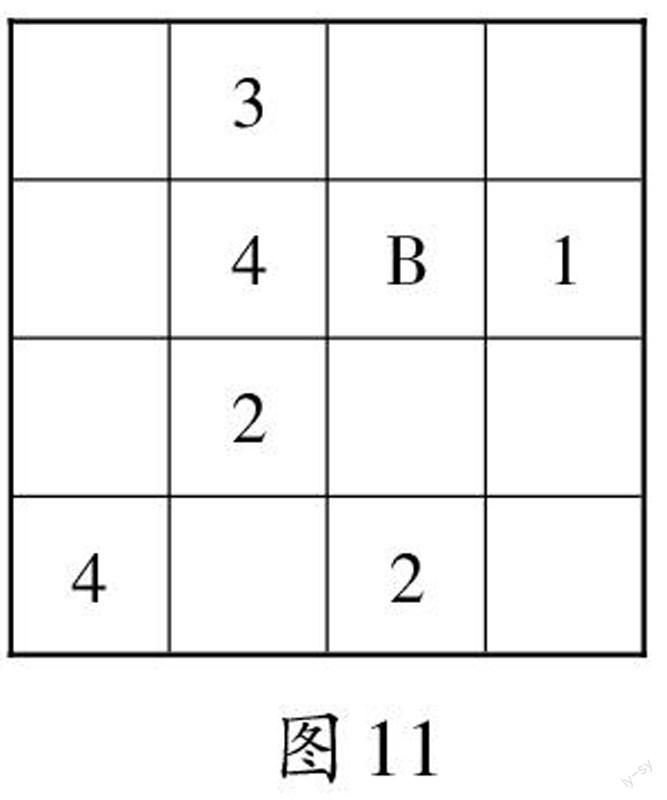
师（反馈直接的填数方法，如图11）：第二行第二列的数直接定为4，这样B就能定为3，推断思路是什么？

师（反馈间接的填数方法，如图12）：第二列第四行的數可以直接定为1，但这个1无法成为推断B的线索。（如果学生提出第四列第四行的方格填3的说法，处理方式同上）

师：如果我们先确定的数无法成为推断B的线索，那该怎么办？

生₃：只能重新寻找新线索。

师：虽然新指出的1或3对于推断B处的数没有用，但是对于复原整个数表还是有用的。

【对比性反思】此环节的目标仍是引导学生学会判断第一步可确定的数，然后分析首次确定的数是否能成为确定B的线索。假如初次填数失败，还可以调整思路，寻找新的数，直到能顺利确定B。这正符合推理的逻辑程序，而非像教材一样：先确定A，然后判断A是否是推断B的线索，最后再进行调整。真正的推理不需要人告知推理经过，而是根据不全的信息不断去补全信息，这个过程需要不断猜测、尝试、验证，并进行自我纠正和不断调整。显然，在第一次教学中，习题暗示性太明显，基本告知了推理经过；第二次教学时将A隐去，这样学生的推理才是严格的推理，学生的推理能力才能提高。

推理能力的形成不是一蹴而就的，教材出示的例题推理难度过大，部分教师急于求成，巴不得一次性通过讲解代替学生推理，认为这样学生能模仿推理，从而掌握推理方法，其实这样只会适得其反。学生的思维往往跟不上教师的节奏，对此，教师应放慢脚步，从引导者变为启发者，从领路人变为指路人，真正还课堂于学生，让学生去主动推理，从而让学生的推理能力得到有效提升。

（责编 黄春香）