发展学生几何直观能力的对策举隅

钱国华

［摘 要］几何直观能力包括形象思维能力、直观洞察能力、用图形分析问题的能力和空间想象力。教师可在数学教学中运用直观模型、数学操作、数形结合、多媒体设备发展学生的形象思维、直观思维、分析能力和空间想象力，从而提升学生的几何直观能力。

［关键词］几何直观；形象思维；数形结合；空间想象力

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2022）29-0072-03

几何直观主要指用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简单，有助于学生找到解题思路。由此可见，几何直观的价值在于将抽象问题化为具体问题，以促进学生对数学知识的理解，提升学生分析和解决问题的能力。

从具体内涵来看，几何直观能力包括形象思维能力、直观洞察能力、用图形分析问题的能力和空间想象力，这些能力在学生的学习过程中起着重要的作用。需要强调的是，几何直观能力同时面向观察、判断与思维能力。学生在生活中看到的图形，很多都不是他们在课本上看到的几何图形，学生需要在观察的基础上进行抽象，才能得到他们熟知的几何图形，得到几何图形后还要对其进行判断，再通过思维的加工，才能形成直观认识。这个过程是非常复杂的。教师要认识到其中的复杂性，然后设计一个有效的教学方案，才能切实有效地发展学生的几何直观能力。笔者以此为据，结合教学实践，提出在数学教学中发展学生几何直观能力的对策，期望能够起到抛砖引玉的效果。

一、借助直观模型，发展学生的形象思维

把抽象的数学问题以图形的形式呈现出来，有利于学生理解问题。教师要引导学生把抽象的数学问题转化为直观模型，或者直接在现实生活中找到与问题有关的直观模型，通过直观模型将数学问题具体化、形象化，才有利于增强学生的直观感受，促进学生对问题的深度理解。

比如，在教学“解决问题的策略”时，教师出示了这样一道题：六（1）班有10名学生进行乒乓球比赛，每2名学生要比一场，一共要比多少场？

生₁：可以先找规律。我采用列表法（如表1），通过表格不难看出，当有2名学生比赛时，要比1场；当有3名学生时，要比1+2=3（场）；当有4名学生时，要比1+2+3=6（场）……按照这样的规律，当有10名学生时，要比1+2+3+4+5+6+7+8+9=45（场）。

生₂：有了这个表格，我们就可以轻松地解决问题了。

生₃：我是画图分析的（如表2），可以得到和列表法相同的结论。

师：如果参加比赛的学生人数很多，那么无论是用列表法还是画图分析，都比较麻烦。我们是不是可以从表格或示意图中总结出一般的原理呢？

[学生讨论，并在教师的引导下得出公式：比赛场数=n×（n-1）÷2（n为参加比赛的人数）]

在思考和表达的过程中，学生采用了列表和画示意图的方式建立直观模型，这就把抽象、复杂的数量关系直观地呈现了出来。学生通过观察和分析直观模型，得出比赛人数和比赛场数之间的关系，由此顺利解决问题。学生在这个过程中发展了形象思维。在没有表格和示意图的时候，学生思维加工的对象只能是文字，而有了几何图形之后，学生思维加工的对象就是几何图形。这样一个转换既是学习内容的转换，也是思维方式的转换——学生的思维由抽象思维转换为形象思维，而这符合小学生的思维特点。这样的转换降低了解题难度，更容易让学生发现规律。因此，幾何直观的模型有利于学生学习数学知识，同时能有效发展学生的形象思维能力。

二、借助数学操作，发展学生的直观思维

直观思维指的是人们不经过缜密分析，就迅速对问题的答案做出合理的猜测、设想的一种跃进性思维。直观思维并非凭空猜测，而是以知识储备和认知经验为基础的大胆合理猜测。学生要发展直观思维，离不开动手实践和操作。心理学家皮亚杰说：“活动是认识的基础，智慧从动手开始。”数学操作顺应了小学生活泼好动的性格特征，有利于激发学生的学习兴趣。此外，数学操作可以调动学生的感官，使学生更好地参与到数学活动中，感知大量直观形象的事物，获得丰富的认识，并在活动过程中发展学生的直观思维。

比如，在教学“两位数除以一位数”时，教师出示了算式“42÷2”，并要求学生通过数学操作（摆小棒）进行计算。学生自主摆小棒，借助操作探究算法。

师：你能用自己的话表述自己的操作过程吗？

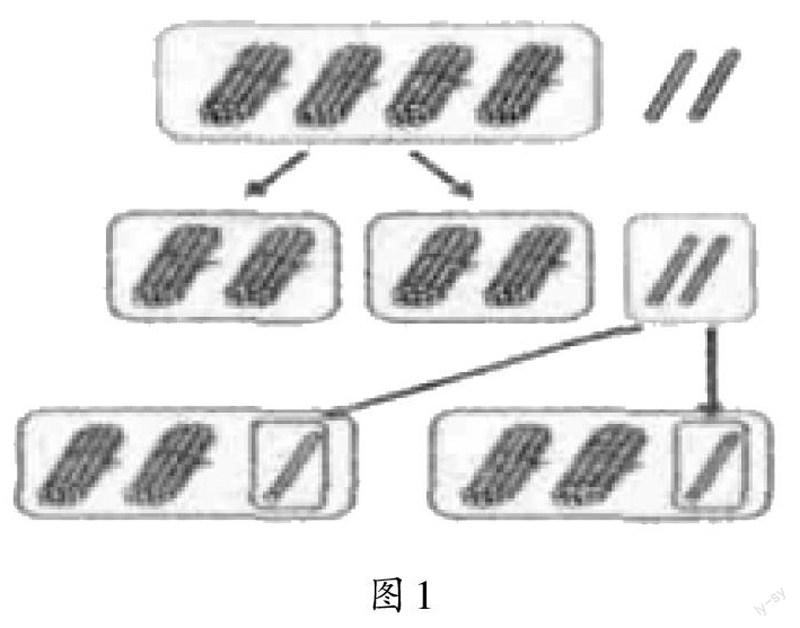
生：我先把4捆小棒（1捆10根）平均分成2份，每份是2捆，即2个十，再把2根小棒平均分成2份，每份是1根，即1个一，2个十和1个一加起来就是21，因此，42÷2=21（如图1）。

教学中，教师引导学生采取摆小棒的方式探究两位数除以一位数的算理，学生在摆小棒的过程中建立了直观操作和除法算式之间的内在联系，并在摆一摆、数一数的过程中发展了直观思维。以上教学最大的特点就是学生有了动手操作的机会。从表面上看，学生只是在动手，实际上学生是手脑并用。学生的操作并不是无序的，而是围绕学习内容进行的有序操作，之所以有序，是因为背后有思维在驱动。数学操作能够很好地将学生的手、脑融合在一起。学生要动手又动脑，才可以有效建构数学知识，发展直观思维。

三、运用数形结合，发展学生的图形分析能力

用图形分析问题的能力是几何直观能力的重要组成部分，而要发展学生的图形分析能力，可以运用数形结合的方法。数学家华罗庚说：“数无形时少直觉，形少数时难入微；数形结合百般好，隔离分家万事休。”可见数形结合在数学学习中有重要的价值。数形结合把抽象的数和直观的图形结合起来，不但能促进学生理解数学，还能提高学生的解题能力。

比如，在教学“排队问题”时，教师出示这样一道题：小动物们排成一排看电影，从右边数，小兔子是第4只，从左边数，小兔子是第6只，一共有多少只小动物？虽然该题的难度不大，但是一年级学生对纯文字题的理解能力比较弱，且题中涉及左右两个方向，这就给学生解题造成了不小的困难。此外，有的学生虽然能够计算出结果，但是难以说明其中的道理。针对这种情况，教师引导学生采取数形结合的方法，让学生用画图的方式解决问题。其中，一名学生根据题意画图（如图2）：用圆圈代表其他小动物，用正方形代表小兔子，从右边数，小兔子是第4只，就在正方形的右边画3个圆圈；从左边数，小兔子是第6只，就在正方形的左边画5个圆圈。这样就得出一共有4+6-1=9（只）小动物。

在此基础上，教师巧妙变换题目：小动物们排成一排看电影，小兔子的右边有4只小动物，小兔子的左边有6只小动物，一共有多少只小动物？有了之前的画图经验，学生很快地画出了图形（如图3），并列出算式：4+6+1=11（只）。

在教学中，教师引导学生通过画图的方式解决问题，把抽象的数量关系转化成直观的图形。通过画图和读图，学生很容易从图形中提取其中暗含的数量关系，从而快速理解题意和解决问题。学生运用图形分析问题、解决问题的能力得到了锻炼和发展。数形结合是数学中的优秀方法，教师运用此方法教学，不仅能够有机地将学生的形象思维与抽象思维融合在一起，而且能够帮助学生形成用图形分析问题的意识。教师要充分把握学生的认知特点，努力为学生创设一个良好的數形结合的情境，用学生熟悉的图形去撬动学生的思维，从而有效发展学生的几何直观能力。

四、运用多媒体，发展学生的空间想象力

空间想象力是几何直观能力的重要组成部分。笛卡尔说：“没有图形就没有思考。”数学课程标准明确指出：要使学生逐步掌握简单几何形体的形状、大小和位置关系，能够识别所学的几何形体，并能概括几何形体的名称，再现它们的表象，培养学生初步的空间观念。多媒体技术被广泛应用于教学之中，为教师培养学生的几何直观能力提供了新的途径。目前，课堂上常用的多媒体软件和设备有几何画板、IT图形计算器、交互式智能白板等，这些软件和设备不仅有效激发了学生学习数学的兴趣，而且高效地将抽象难懂的数学问题转化成直观的形式后呈现出来，较好地促进了学生空间想象力的发展。

比如，在教学“认识长方体”时，教师运用多媒体教学，带领学生认识长方体。

师：同学们，请看屏幕上的是什么？

生₁：一张纸。

师：如果我把很多张纸叠起来，会是什么样的呢？

（教师运用多媒体课件展示把一张张纸叠起来，最终形成长方体的动态过程）

生₂：变成了一个长方体。

生₃：把一个个平面叠起来就变成了立体图形。

师：对。数一数，长方体一共有几个面？

生₄：6个。

（使用多媒体让长方体的6个面变亮）

师：同学们数一数，长方体有几组棱，一共有几条棱？

生₅：有3组棱，一共有12条棱。

（使用多媒体让长方体的棱变亮，且每一组棱的颜色不同）

师：同学们再数一数，长方体有几个顶点？

生₆：8个。

（使用多媒体让长方体的顶点变亮）

教学中，学生通过多媒体课件观看一张张纸叠成长方体的过程，看到了平面图形到立体图形的转变。教师通过多媒体课件引导学生认识长方体的面、棱和顶点等各部分，给予学生强烈的视觉刺激，这不但调动了学生的兴趣，激发了学生的空间想象力，还促进了学生几何直观能力的发展。

小学阶段是培养学生几何直观能力的关键时期。随着课程改革的不断深入，数学课堂会出现大量的直观图形，也会穿插很多剪一剪、拼一拼的操作活动，其目的就是要不断发展学生的几何直观能力。教师要转变教学观念，以教学内容为载体，用几何直观架构一座连通具象与抽象的“桥梁”，引导学生借助直观的图形分析和解决问题，不断提升学生的几何直观能力。

［ 参 考 文 献 ］

[1] 徐晓庆.小学数学几何直观教学的策略[J].江西教育，2021（9）：43-44.

[2] 符明.借助几何直观   理解数的运算[J].小学数学教育，2021（6）：12-13.

[3] 王燕.建构“直观思维”：几何直观教学的重要使命[J].数学教学通讯，2020（31）：28-29.

[4] 周波，牟天伟.聚焦几何直观，培养核心素养：小学五年级“画图策略”例谈[J].教育科学论坛，2020（28）：39-43.

（责编 黄 露）