点子图：让计算学习既知“书”又达“理”

冯刚

［摘 要］两位数乘两位数的竖式模型较为抽象且不易理解，要正确建构竖式模型的前提是掌握算法（知“书”）和理解算理（达“理”）。在教学“两位数乘两位数（不进位）”时，引导学生在生活中抽象出点子图，借助点子图这一直观模型探索口算拆分方法、抽象竖式模型，并在点子图、口算与竖式的关联比较中建构竖式模型，让学生的计算学习既知“书”又达“理”。

［关键词］点子图；竖式；算理；算法

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2022）29-0063-03

兩位数乘两位数的笔算既是两位数乘一位数笔算内容的后续知识，又是三位数乘两位数的前置知识，在数的运算教学中起着承上启下的作用。在三年级上学期，学生已经学习了两位数乘一位数的口算，在“两位数乘两位数（不进位）”的前一课，学生已经学习了两位数乘整十数的口算。教材这样编排，意图非常明晰，即教学时应基于学生的已有认知，将本课内容与先前所学的两位数乘一位数、两位数乘整十数的口算相关联，引导学生在同化与顺应中实现知识的自我建构。

然而，由于学生尚未学习乘法分配律和乘法结合律，因此将两位数乘两位数的计算转化为两位数乘一位数及两位数乘整十数的计算，对学生来说就显得抽象且难于理解，将口算与列竖式笔算环节建立联系更是困难重重。为此，多数学生仅了解竖式的“形”而并未理解竖式的“实”，对两位数乘两位数仅仅是知“书”——知道其书写格式和规范，而并未达“理”——理解运算背后的算理。如何使得这个转化过程显得直观且易于理解，并为后续竖式模型的建构提供支撑，让学生从机械记忆层面过渡到理解学习层面，实现既知“书”又达“理”，是本课教学亟须解决的问题。

笔者在查阅众多版本教材后发现，人教版教材和北师大版教材均采用了点子图这一直观模型，提倡通过直观的点子图引导学生进行思考和探索。为此，在教学中，笔者借助点子图这一直观模型引导学生在自主探索与合作交流中理解口算拆分方法及竖式计算方法的合理性，以促使学生发现口算拆分方法与竖式算理上的一致性，进而在理解算理的基础上建构竖式模型，实现既知“书”又达“理”。

一、抽象点子图，理解图示本质

点子图是学生探究多样化算法的直观图示，有利于学生理解算理，可谓是实现知“书”达“理”的一剂良药。然而，这样一剂良药是否真能做到“药到病除”，帮助学生实现抽象算理的直观化，仍有待实践验证。为此，笔者对学生进行了前测调查，发现这剂良药的效果并不理想：陌生且抽象的点子图并不受学生欢迎，学生也未能在点子图、算理与算法间建立联系。究其原因，是点子图脱离了学生的实际生活，抽象且难以理解。对此，笔者从学生熟悉的队列方阵中抽象出点子图，引导学生经历点子图的形成过程，以便学生理解与应用点子图。

【教学片段1】

师：三年级是人生一个重要的阶段，而三年级的小朋友正好是十岁，学校要为小朋友们举行一场成长礼。其中有一个节目，需要小朋友排成一个方阵来进行啦啦操表演。

师（出示方阵图，图略）：观察方阵图，你们能告诉我该怎么列队吗？

生₁：人太多，队伍很挤，通过现在的方阵图数不清楚每排有几个人。

师：数学讲究的是简洁清楚。有没有什么办法既能让大家看清人数，又不改变方阵的形状？

生₂：可以用一个圆点代替一个人。

师：就听你的！

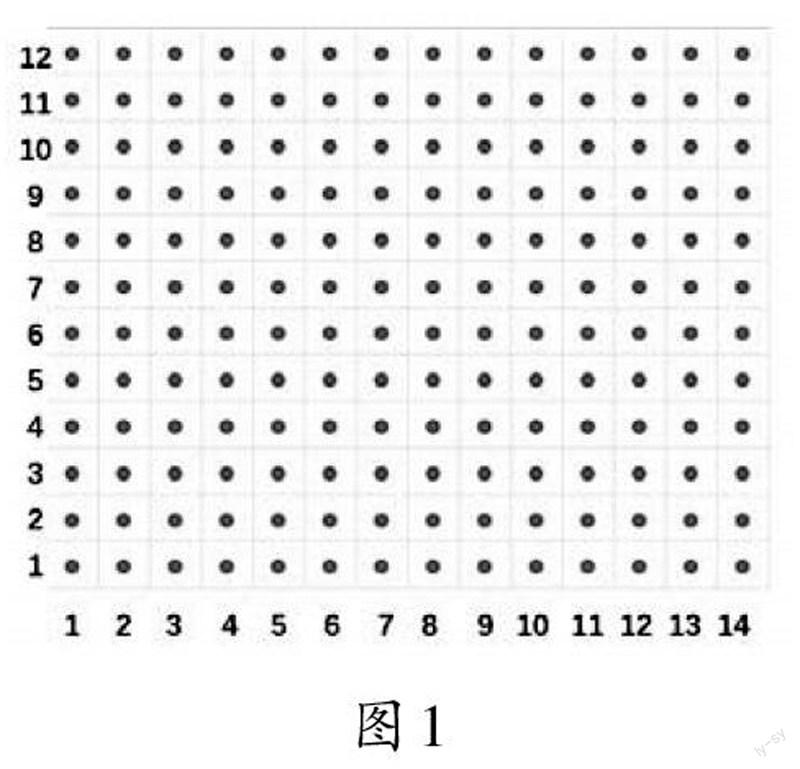
师（出示点子图，如图1）：从点子图中你看出了哪些数学信息？

生₃：每排有14人，另一边每排有12人。

师：也就是说每行有14人，有这样的几行？

生₄：12行。

师：谁能完整地说一遍？

生₅：每行有14人，有12行。

师：根据这些信息，谁来提一个数学问题？

10岁成长礼是学生人生中的重要仪式，贴近学生的生活实际，易于激发学生的学习热情。在真实的方阵图中，密密麻麻的人群分布不易于学生发现人员的排列规律。由此，学生自然而然产生简化的想法。基于这样的真实需求，笔者巧妙地将真实的方阵图抽象为点子图，由抽象的点子图再提出实际问题，直观与抽象的相互转换，一方面有助于学生深入理解点子图的本质，另一方面，使得学生的抽象能力和符号意识得到了发展。

二、圈画点子图，探索多样算法

在教学本课前，学生已经掌握了两位数乘整十数及两位数乘一位数的计算方法。根据皮亚杰的发生认知论可知，这些已有认知是学生进行同化和顺应的基础和前提。但是，将两位数乘两位数转化为两位数乘整十数、两位数乘一位数的算理依据是乘法分配律与乘法结合律，而学生尚未学习这两种运算律，这就成了新知转化过程中的阻力。如何将抽象的算理直观化，如何巧妙化解这样的阻力，帮助学生直观地理解算理，是亟须解决的问题。为此，借助抽象出来的点子图，以点子图这一直观图示巧妙绕开运算律的障碍，可以让学生的转化过程自然顺畅且易于理解。

【教学片段2】

师：14×12的结果究竟是多少呢？请拿出研学单，按研学要求开始探索吧！

出示研学单：

（1）用你喜欢的方法计算14×12。

（2）在点子图中圈一圈、画一画，表示出你的计算方法。

（3）你还能想到其他方法吗？

生₁：14×2=28，14×10=140，140+28=168。（如图2-1）

生₂：14×6=84，84×2=168。（如图2-2）

生₃：14×4×3=168。（如图2-3）[14×2=28

14×10=140

140+28=168][14×6=84

84×2=168]

师：瞧，经过我们的研究，得出了这么多不同的方法。你们有没有想过，为什么一开始不好算的14×12，现在口算就算出来了呢？是怎么做到的？

生₄：本来是两位数乘两位数，现在变成了两位数乘一位数或两位数乘整十数。

師：像这样把不太会做的变成已经学过的东西，我们就把它称为转化。转化这一方法能把复杂的问题变成简单的问题。

看着点子图说一说不同的算法，其本质是借助图示直观地解释运算过程，进而深入理解算理。此外，借助点子图这一直观图示来解决问题，学生既感受到了数形结合思想在解决问题时的形象性，也体会到了转化思想在数学学习中的重要性，数学思想和数学思维均得以发展。

三、借助点子图，抽象竖式模型

要想深入理解算理，学生必须理解笔算中每一步计算结果的含义，明确每一步计算结果背后的算理。为此，可以借助点子图这一直观素材，尝试将竖式计算过程中的每一步竖式表征与图形表征同步演绎，促进学生对竖式中各部分结果意义的理解。将点子图引入笔算教学，就是应用数形结合引导学生亲历两位数乘两位数竖式模型的建构过程。在这样的过程中，学生对算理的感性认识已然上升到对方法的理性认识。“法中见理，理中得法”，实现知“书”的同时也将达“理”落到实处。

【教学片段3】

师：对于14×12，请说说你是怎么想的。

生₁：2×4=8，2×1=2。

师：为什么8写在个位上，而2写在十位上呢？

生₁：2×1实际上代表的是2×10，得到的2表示的是2个十，所以2写在十位上。

生₂：十位的1×4=4，4写在十位上，1×1=1，1写在百位上。

师：你怎么知道4要写在十位上呢？

生₃：这个1是1个十，1个十乘4就是4个十。

师：是的，十位上的4表示40，我们一般不写0。那1为什么写在百位上呢？

生₄：这里实际上是10×10=100。

师：说得真好！最后应该怎么算？

生₅：最后算8+0=8，2+4=6，0+1=1。

师：为什么最后用加法而不是乘法呢？

生₆：因为要将两部分合起来。

师：是的，28表示2行的人数，140表示10行的人数，最后加起来就是12行的人数。

师：由此，我们用竖式也算得结果是168。（出示图3）图中我们看到了168，不过，竖式计算时要将数位对齐，图中对齐了吗？让它对齐好不好？（出示图4）看这个图，你有什么感觉？

在竖式模型的建构过程中，每一步运算的结果均能在点子图中找到对应的位置，将抽象的运算与直观的点相关联，化抽象为直观。学生借助直观图能很好地理解两位数乘两位数的顺序，以及每次运算后积的表征及积的书写位置，初步掌握了两位数乘两位数计算算法背后的算理。而让学生将点子图进行数位对齐，并观察其变化，能进一步将抽象的竖式模型以直观的形式呈现在学生面前。学生能将抽象的竖式模型与直观的点子图模型相关联，自然就能化抽象为直观，于直观中思抽象，竖式模型便深深扎根于脑海中。

四、关联点子图，建构竖式模型

南京大学的郑毓信教授曾说：“数学知识不求全，而应求联。” 竖式本质上是对计算过程的记录，换言之，竖式本质上是口算算式和过程的另一种表达方式，是针对复杂计算而归纳出的一种计算模型。既然竖式模型的建构与口算拆分方法有着密切的联系，唯有将两者相关联，抽象的竖式模型才能牢牢建构于学生的头脑中。为此，将点子图、横式与竖式计算的每一步相关联，在三者的联系与对比中，笔算算法形成的脉络和算法的合理性得以进一步凸显，学生就能在知“书”达“理”的基础上建构竖式模型。

【教学片段4】

师（出示图5）：请大家继续观察，竖式与这里的口算，以及对应的点子图有没有什么联系？

生：竖式里的28就是口算的第一步，表示2行的人数，14就是口算的第二步，表示10行的人数，最后的168就是口算的第三步。

师：是的，竖式其实就是将三道口算题综合到一个竖式里面，这样计算就更加简便。

通过在点子图、横式与竖式三者之间建立联系，抽象的数与直观的形得到有机结合，学生对算理的理解自然也就有“形”可依。而通过对点子图、横式与竖式三者的综合对比和分析，竖式模型中三步计算的过程在学生的头脑中变得清晰有序。学生经历了抽象算理到直观算法的演绎过程，在数形结合中实现对算理的深刻理解，达成对算法的理解和掌握，真正建构两位数乘两位数的竖式模型。

对算理的深入理解与对算法的熟练掌握是学生运算能力得以提高的前提。两位数乘两位数的竖式模型是学生后续进一步学习笔算的基础。教师在教学中应基于学生的已有认知，巧妙依托点子图进行教学，让学生的计算学习既知“书”又达“理”。

［ 参 考 文 献 ］

[1] 于正军.例谈两位数乘两位数笔算乘法的困惑解析与算法建构[J].教学与管理，2015（29）：51-53.

[2] 侯正海.运算能力形成的过程：以“两位数除以一位数的笔算”教学为例[J].小学数学教育，2020（6）：56-58.

（责编 金 铃）