从前测到对策，精准教学的必由之路

陈琳

［摘 要］前测对教师精准把握学情具有重要意义。以“平行四边形的认识”为例，文章从四个方面阐述了基于前测的小学数学教学路径，力图最大限度地整合教学资源，改进教学方法，进而实现精准教学。

［关键词］前测；平行四边形；精准教学

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2022）29-0054-03

前测不仅是教师评估学生学习起点的重要途径，也是教师在把握学情基础上设计教学活动的基本依据。唯有充分发挥前测的“把脉”作用，教师才能真正实现“备课本、备学生”的备课理念，才能针对前测制订教学计划，从而更好地精准教学。笔者以“平行四边形的认识”为例，在前测的基础上设计教学活动，力图最大限度地整合教学资源，改进教学方法，实现精准教学。

一、精心设计前测，精准把握学情

美国著名教育心理学家奥苏泊尔曾经说过：“影响学习的最重要的因素是学生已经知道了什么，我们应当根据学生原有的知识状况去进行教学。”那么，怎样才能读懂学生呢？前测无疑是行之有效的办法。首先，前测有利于教师了解学生的前概念，找准教学切入点。学生理解一个新概念，往往是以前概念作为支撑的。教师把握学生的前概念，就能够精准找到新概念教学的切入点。其次，通过前测，教师能全面而真实地了解学生的信息，发现学生在学习和思考中的一些共性问题，这样，在教学环节就能够有的放矢、对症下药。最后，前测能够帮助教师辨别学生的差异。在过去，教师对学生的研究往往是从学生的年龄特征和身心特点入手，但学生是一个个具体的、独特的个体。而通过前测，教师能够动态地、精准地了解学生，将“心中的学生”转化为“现实中的学生”，从而使教学由粗放转向精细，提升教学的针对性。

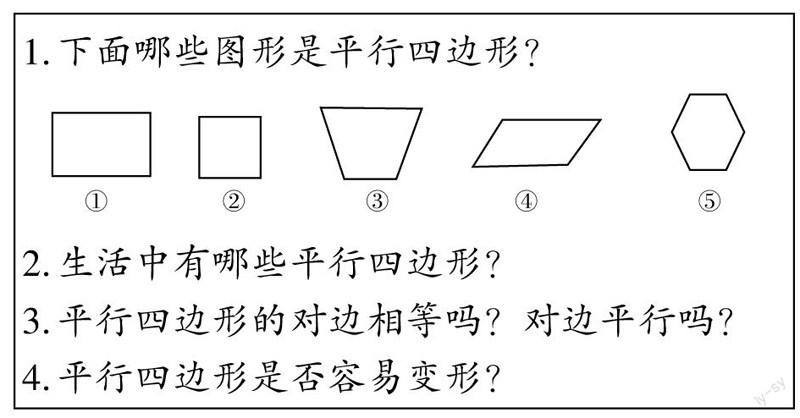
比如，“平行四边形的认识”一课，可设计这样的前测内容：

前测结果显示，对于第1题，超过90%的学生能判断出④属于平行四边形，由此可以得出，学生对基本的平行四边形的形状已经具有了一定的认识；超过80%的学生能够判断出⑤不属于平行四边形，由此可以得出，学生对平行四边形都是四边形有比较准确的认识；但仍有35%的学生认为③也属于平行四边形，由此可见，学生对平行四边形的概念把握不准确；大约60%的学生认为①和②不属于平行四边形，这说明学生对长方形、正方形和平行四边形之间的关系的认识存在含糊不清的情况，是学生认知中的“盲点”，需在教学中予以强化。

对于第2题，学生大多都能说出两种生活中的平行四边形，比如伸缩门、升降架、伸缩晾衣架等。由此可见，学生对平行四边形具有初步认知，已经具备学习平行四边形的生活经验。

对于第3题，超过80%的学生认为平行四边形对边平行，但是对平行四边形对边是否相等，学生有不同的认知。30%的学生认为平行四边形的对边不相等，因此可以判断，平行四边形对边相等是学生认知上的一个难点。

对于第4题，超过50%的学生认为平行四边形的形状是稳固的，并不容易变形。由此可见，学生对平行四边形的不稳定性认知不清。这主要是由于学生对稳定性的含义理解不到位造成的，这是学生认知上的另一个难点。

通过对前测的整体分析可以得知，教学中应当突出对平行四边形对边相等、长方形和正方形都属于平行四边形、平行四边形的不稳定性等问题的探索和强化。

二、积累直观经验，初步感知概念

胡塞尔曾经说过：“生活世界是自然科学被遗忘的基础。”当学习材料源于生活或者与现实生活密切结合时，这样的数学才是“活”的，才是充满生命力的。因此，教师要沟通数学知识与现实生活的联系，寻找数学模型在现实生活中的原型，帮助学生积累直观经验，进而初步感知概念。通过前测可知，学生已经初步积累了平行四边形的相关经验，这就为教师从学生的生活经验中引出平行四边形奠定了認知基础。

【教学片段1】

师：生活中，有很多平行四边形，请说一说你见过的平行四边形。

生₁：学校的电动伸缩门就是平行四边形的形状。

生₂：伸缩晾衣架里也有平行四边形。

生₃：楼梯扶手也是平行四边形。

师：对。看来我们身边的平行四边形还真不少。那么，什么是平行四边形？平行四边形有哪些特点呢？让我们一起来探索吧。

把教学内容置于生动的教学情境之中，可以激发学生的探究欲望。因此，在导入环节，教师可引导学生多举几个日常生活中平行四边形的例子，进一步丰富学生的认知，这样既能很好地对接学生已有的认知经验，又能达到导入新课的目的。

三、经历探究之路，促进认知发展

苏霍姆林斯基说：“在人的内心深处，都有一种根深蒂固的需要，就是希望自己是一个发现者、研究者和探索者，而在儿童的内心世界中这种需要尤为强烈。” 针对在前测中暴露出的学生认知上的误区和难点，教师在教学时应该让学生经历知识探索的过程，感悟知识产生的真实过程，只有这样，学生才能获得深刻的理解，才有利于长时记忆。此外，一波三折的探索过程，也十分有利于培养学生肯探索、敢探索的精神，使学生养成主动探索的好习惯。

【教学片段2】

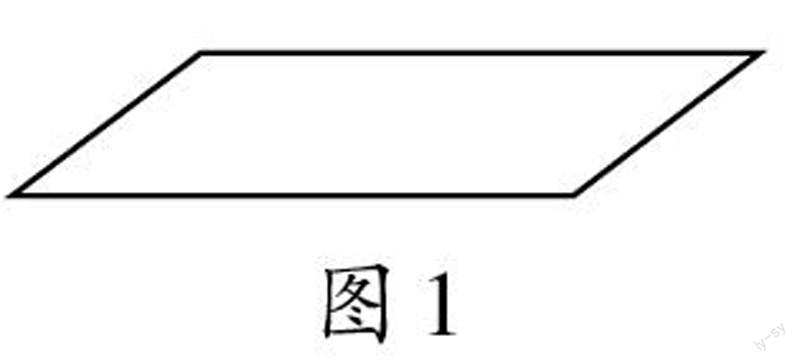
师：图1是一个平行四边形，大家说一说，为什么叫它平行四边形呢？

生₁：因为它由四条边组成。

生₂：它的对边是平行的。

师：那我们如何来验证它的对边平行呢？现在请以小组为单位讨论一下吧。

生₃：我们在平行四边形上下两条对边上画了2条垂直的线段，通过测量发现，2条垂线段的长度相等；同时，我们在平行四边形左右两条对边上画了2条垂直的线段，我们发现这2条垂线段的长度也相等。因此，平行四边形两组对边互相平行。

生₄：为什么2条垂线段的长度相等，就说明对边平行呢？

生₃：因为平行线之间的距离相等。

师：生3是通过画垂线段的办法来验证平行四边形两组对边互相平行的。还有其他办法吗？

生₅：我们把平行四边形的对边延长，发现它们不相交。由此我们得知，平行四边形的两组对边互相平行。

师：非常棒。通过画垂线段和画延长线的办法验证了平行四边形对边互相平行。现在谁能概括一下什么是平行四边形呢？

生₆：两组对边互相平行的图形是平行四边形。

生₇：不对，还应该加上“四边形”这个前提。

师：对，两组对边互相平行的四边形叫平行四边形。

师：平行四边形的对边是互相平行的，那么，它们是否相等呢？

生₈：两组对边的起点和终点不一样，很难准确判断。

师：我这里有三组小棒。第一组小棒的长度分别为7厘米、7厘米、5厘米、5厘米；第二组小棒的长度分别为7厘米、7厘米、3厘米、5厘米；第三组小棒的长度分别为7厘米、6厘米、5厘米、4厘米。下面请三个小组分别用这三组小棒试着摆三个平行四边形，看看能否成功，记得要分析原因。

生₉：我们组用的是第一组小棒。我们用长度相等的两根小棒作为对边，很容易就摆成了一个平行四边形。

生₁₀：我们组用的是第二组小棒。无论我们怎样摆放，也无法将小棒摆成一个平行四边形。我们认为，是由于一组对边长度不一样导致的。

生₁₁：我们组用的是第三组小棒。与第二组一样，不管我们怎样摆放，都无法将小棒摆成平行四边形。我们认为，这主要是因为两组对边的长度都不一样导致的。

师：通过操作发现，只有两组对边相等的小棒才能够摆成一个平行四边形。

根据前测结果，教师在课堂中要引导学生以小组探究的方式进一步验证猜想、深化认知。学生通过画垂线段和画延长线，认识到了平行四边形的对边是平行的，同时通过操作和对比，体会到平行四边形的两组对边不仅平行，而且在长度上是相等的。

四、联系生活再认识，知识建构促提升

针对学生对平行四边形不稳定性的认知还存在欠缺的现象，教师应当引导学生联系现实生活来感悟平行四边形的易变形和不稳定性，并在此基础上引导学生通过实验操作进一步理解平行四边形不稳定性的本质。另外，针对学生不能正确把握平行四边形与以前所学的长方形、正方形之间的关系这一问题，教师在教学中要致力于打通这三个图形之间的关联，使学生将新知识建构在已有知识基础上，最终完善学生的知识建构。

【教学片段3】

师：在生活中，伸缩门、伸缩晾衣架和升降机都被设计成了平行四边形的形状，为什么要这样设计呢？平行四边形暗含了什么样的独特性质呢？

生₁：平行四边形不稳定，容易变形。

生₂：不对呀，我做的这个平行四边形的四条边粘得很稳定，它根本就不会变形。

师：那么，究竟什么是稳定性呢？为什么说平行四边形容易变形呢？我们还是通过操作实验来探究。我这里有三组小棒：每一组4根小棒的长度分别是10厘米、10厘米、6厘米、6厘米。下面请三个小组分别用其中的一组小棒搭建平行四边形，看看它们搭建的平行四边形形状一样吗？

生₃：我们组搭建的平行四边形是向右边倾斜的（如图2-1）。

生₄：我们组搭建的平行四边形就快要“立”起来啦（如图2-2）。

生₅：我们组搭建的平行四边形是向左边倾斜的（如图2-3）。

师：用完全一样的4根小棒，却搭建出了不同形状的平行四边形，说明了什么呢？

生₆：說明平行四边形的形状易变。在各个边的长度都固定的情况下，它的形状却是千变万化的。

师：对，这就是平行四边形的不稳定性，它很容易变形。生活中的伸缩晾衣架、伸缩门就是利用了平行四边形容易变形的性质。

在该教学片段中，教师通过引导学生利用小棒搭建平行四边形的方式证明了平行四边形具有不稳定性。传统教学中，教师采取让学生拉动平行四边形的办法来验证它的不稳定性，但学生会产生新的疑问：把平行四边形的四条边都粘接好，它是不是就不会再变形了？而采用案例中的操作方法，学生更容易理解平行四边形的不稳定性，从而较好地突破这一学习难点。

【教学片段4】

师：这几个图形中，哪些是平行四边形？

生₁：⑤不是四边形，因此它不是平行四边形。

生₂：④是平行四边形，它的两组对边平行且相等。

生₃：③不是平行四边形，它只有一组对边平行。

生₄：①和②也不是平行四边形。

生₅：不对，①和②满足平行四边形的定义，它们都是两组对边平行的四边形，为什么不是平行四边形呢？

生₄：看来①和②也属于平行四边形。

生₆：这种平行四边形不是“斜着”的。

师：对，长方形和正方形属于特殊的平行四边形，它们满足平行四边形的定义，也具备平行四边形的所有特点。只不过长方形和正方形不是“斜着”的平行四边形，而是“站直”了的平行四边形。

在该教学片段中，教师通过引导学生辨析，使学生认识到长方形和正方形也是平行四边形，在此基础上，再引导学生把平行四边形知识纳入已有的认知体系中，进而使得学生对平行四边形产生了整体性认识。

总之，前测是教师把握学情的基础，也是实现精准教学的现实需要。只有充分掌握学生的“数学现实”，教师才能使教学活动更有针对性，从而使得数学课堂务实高效。

（责编 金 铃）