提升学生数学模式识别能力的策略

孟令艳

[摘  要] 在高中数学教学中有一个基本任务，那就是提升学生数学学习与问题解决中的模式识别能力. 如果教师认同模式识别的价值，在教学中能够用模式识别的思路引导学生解决问题，那么学生模式识别能力的养成也就有了更大的空间. 模式识别能力的培养策略可以概括为：给学生创设问题解决的情境，让学生在分析问题条件的过程中，建立起与自身数学知识体系相关的联系. 这样一个联系建立的过程，就是模式识别的过程. 本着循序渐进的思路，在模式识别能力培养的过程中，让问题逐步从单一走向开放，学生的思维触角就可以向更多的知识漫溯，识别的空间也就更大，模式识别能力也就能得到递进式培养.

[关键词] 模式识别;能力提升;教学策略

任何一个知识的学习都与学生的学习心理规律相关，反之，只有遵循学习心理规律的教学，才是最适合学生的教学. 就拿高中数学教学来说，要让学生掌握数学知识，并且利用数学知识去解决问题，尤其是实际问题，很重要的一点就是学生能够发现问题或实际问题与自己所学数学知识之间的联系，这样的发现过程实际上就是识别过程. 如果学生在识别过程中能够带有模式运用的思路，那么这样的识别过程也就成了“模式识别”. 模式识别作为一种在信息科学及自然科学中广泛应用的技术，其重要性是不言而喻的. 将模式识别迁移到数学学科中来，人们发现这一方法在高中数学教学中也能够得到有效应用.

这是符合心理规律的. 当前流行的建构主义学习理论认为，学生学习的过程就是意义建构的过程，而著名教育心理学家奥苏伯尔（D.P.AuSubel）曾经强调：意义学习的过程是新旧意义同化的过程. 他认为：人类之所以能够进行有意义学习，就是因为新知识与他原有的认识结构中的某些观念发生了影响，即所学的新材料和原有的认知结构之间相互作用的结果[1]. 这就表明：当学习主体也就是学生接触到数学问题后，他们会自觉进行一种心理活动，即寻找数学问题与原有的认知结构之间的联系. 而如同上面所指出的那样，这样一个寻求联系的过程，可以用模式识别这一概念来概括. 因此在高中数学教学中就有一个基本任务，那就是提升学生数学学习与问题解决中的模式识别能力. 本文就结合苏教版高中数学“解三角形”的相关知识，来谈一谈模式识别能力的提升及具体策略的运用.

[?]高中数学教学要关注学生的模式识别能力

建立模式识别的概念，然后以模式识别能力的提升作为教学的重要思路，对于高中数学教师来说是非常有效的. 无论是从当前培养学生应试能力需求的角度来看，还是从培养学生数学学科核心素养的角度来看，模式识别都能够在其中发挥重要的作用. 因此数学教师一定要关注学生模式识别能力的养成.

相对于绝大多数学生在数学问题解决过程中表现出来的思路不清晰、解题靠摸索、结果看运气的现状而言，运用模式识别的方法，可以体现数学模式所具有的很强的抗干扰的功能，如透过表象抓本质、透过图形看层次、采集信息分清主次、同中求异、异中求同等. 这就意味着运用模式识别方法的学生，能够在问题解决的过程中更准确地把握数学问题的本质，更精确地寻找到解决数学问题的方法. 数学模式观认为，对一个中学生来说，所谓解题，实际上就是以概念、法则、定理、公式、定律的系统（即数学模式）为准绳，从题目的已知条件和假设出发，按正确的推理和计算，一步步地求出结果和推出结论的过程[2]. 根据这一判断，教师的教学任务就是学生的这种推理能力的发展——这正对应着数学学科核心素养中的逻辑推理要素.

这种能力的养成很大程度上取决于教师，更准确地说，取决于教师的教学理念. 如果教师认同模式识别的价值，在教学中能够用模式识别的思路引导学生解决问题，那么学生模式识别能力的养成也就有了更大的空间. 很显然，拥有模式识别视角且具有相关能力的人，运用数学知识去解决问题的效率更高，所表现出来的数学素养也更高. 因此提升学生的模式识别能力，对于数学教师而言，一定是一个重要的教学任务.

[?]提升学生数学模式识别能力的有效策略

在具体的教学过程中，教师要想方设法地提升学生的模式识别能力，这离不开有效策略的支撑. 有研究表明，无论是在数学问题的解决过程中，还是在实际问题的解决过程中，模式识别能力都源于解决问题的基本经验. 以解决数学习题为例，当学生拿到一道题目后，他们总是先辨别它是否属于已经掌握的题目类型. 如果属于，那么就提取解决该类型题目的方法进行解答;如果不直接属于，那么就会设法进行一些变化;如果无论如何变化都不属于（题目比较陌生或比较复杂），那么就会再考虑其他的途径[3]. 这实际上就是一个模式识别的过程，说得通俗一点，模式识别就是用学生大脑中的模式去识别具体问题，然后再选择相应的问题解决策略.

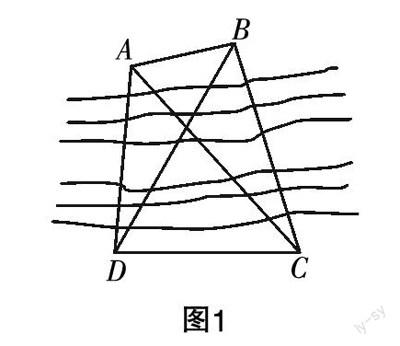
例如，在“解三角形”这一知识的教学中，一个很重要的教学内容就是利用正弦定理和余弦定理去解决相关的问题. 比如有这样一个问题：为了測量某一河流对岸两点A，B之间的距离，某人在河边取两点C，D. 随后测得∠ADC=85°，∠ACD=47°，∠BCD=72°，CD=100 m. 假设A，B，C，D四点在同一平面内，请求出A，B之间的距离.

当问题呈现后，学生的第一反应必然就是去解决问题，而解决问题必须先识别其应当运用哪一数学知识. 尽管学生刚学过正弦定理和余弦定理，但是当面对具体问题而选择解题工具时，还是会有一个相对漫长的模式识别过程. 注意观察学生的解题过程，会发现大多数学生解题的第一步是画图——统计表明，大多数学生所画之图与图1类似. 这说明学生进行数学抽象时，思路是大体相同的. 当学生表现出相近的数学抽象水平时，教学重心也就落在问题解决能力的培养上，而这自然是以模式识别为基础的.

教师教学时可以引导学生去发现：在△ADC中，已经知道了∠ADC和∠ACD的度数，那么就可以求出∠DAC的度数，再结合已知的CD的长度，那么对于△ADC而言，可以运用哪些知识来解决哪些问题呢？通过这样的分析引导与问题的提出，学生必然会在大脑中形成一个对应——一个已知条件与需要解决的问题之间的对应. 而当学生运用正弦定理来解决问题时，实际上也就完成了运用正弦定理这一模型（在数学建模的理解当中，学生运用相对熟悉的数学概念与规律进行问题解决时，概念和规律都是以模型的形态存在的）进行识别的过程. 对于上述问题，还可以进一步以此类推，让学生多次运用正弦定理去解决问题，从而让学生的模式识别能力得到充分培养.

分析上述事例，总结模式识别能力的培养策略，可以概括为：给学生创设问题解决情境，让学生在分析问题条件的过程中，建立起与自身数学知识体系相关的联系. 这样一个建立联系的过程，就是模式识别的过程. 本着循序渐进的思路，在模式识别能力培养的过程中，让问题逐步从单一走向开放，学生的思维触角就可以向更多的知识漫溯，识别的空间也就更大，模式识别能力也就能得到递进式培养.

[?]模式识别能力的提升必须以学生思维为基础

仔细分析模式可以发现，识别在高中数学教学中的作用，主要存在于学生掌握了一定的数学知识后，运用数学知识去解决问题的过程中. 因此，模式识别既是教师重要的教学内容，也是解决数学问题经常用到的策略[4].

本文开头提及模式识别与数学学科核心素养有着密切的联系，很大程度是因为模式识别的培养，跟核心素养强调关键能力的培养是一致的，它们都是指向学生思维的. 在培养模式识别能力的过程中，立足知识的运用，着眼于学生的思维尤其是数学思维，是最基本的原则之一. 事实上，模式识别并不是一个新的概念，早在20世纪90年代就有人做过深入研究. 时至今日，之所以还强调模式识别的价值，正是因为其在发展学生思维的过程中有着不可替代的作用. 而且当下的高中数学教学，以培育学生的核心素养为目标，通过分析可以发现，模式识别能力的培养正是通往数学学科核心素养目标的有效途径.

总而言之，以发展学生的思维为抓手，以模式识别的思路来驱动高中数学课堂教学的发展，可以很好地将学生理解并运用数学知识的意识与能力培养起来，让数学课堂变得更加紧凑，让学生的学习过程变得更加高效，成为促进学生核心素养落地的重要途径.

参考文献：

[1]  黄加卫. 摭談高中数学中的“模式识别”解题策略[J]. 中学数学教学，2008（04）：32-34.

[2]  兰诗全. 数学模式识别与转化策略[J]. 高中数学教与学，2012（12）：35-38.

[3]  罗增儒. 数学解题中的“模式识别”[J].中学数学教学参考，2006（20）：26-28.

[4]  王玉行. “模式识别”与数学分析教学[J]. 数学教育学报，1997（02）：97-99.