以“问”驱研，拓展思维空间

洪静

数学课堂以“问题链”的形式教学，简单地说，就是实施“一题多变、一题多解、多题一解”的教学模式，把固化的问题多点化、灵活化，正向思维变为逆向思维等。本文以苏科版数学七（下）“证明”习题课为例，谈一谈题目变式对培养学生发散性思维的作用。

一、 播下思维的“种”——模型呈现

思维的“种子”是指数学中的基础知识点、基本思想方法与基本技能。教师用思维的“种子”解决数学学习中的基本问题，为培养学生发散性思维打下坚实的基础，在数学基本模型、基本数学方法上实行分类思想，进行方法教学、模型教学。比如，江苏省徐州市铜山区2019年七（下）数学期末试题第26题（如例题）就很好地诠释了这一点。

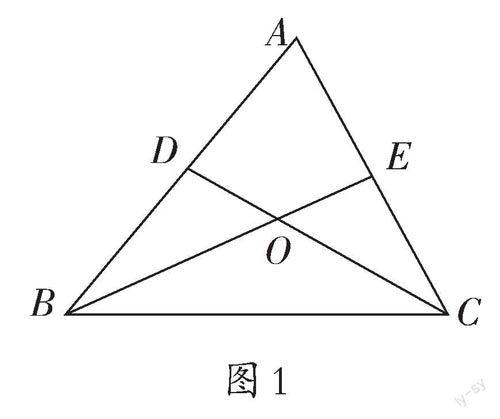
例 如图1，在△ABC中，BE、CD分别为∠ABC、∠ACB的角平分线，交点为O。（1）若∠ABC=70°，∠ACB=50°，求∠BOC的度数；（2）若∠A =40°，求∠BOC的度数；（3）若∠BOC=110°，求∠A的度数；（4）若∠A =n°，求∠BOC的度数。

本题属于问题递进式题目，每一问都层层深入。第（1）问可利用角平分线定义及三角形内角和定理解决；第（2）问在第（1）问的基础上进行了变式，利用三角形内角和过渡，进而解决该问题；第（3）问是第（2）问的逆向思考，条件结论互换位置，步骤相反，培养学生逆向思维能力；第（4）问在第（2）问的基础上，由特殊到一般，只需用n°替代40°就能顺利解决。例题通过这样的设置帮助学生回顾基础知识点，找到思维的“种子”，为后面问题变换的探索做好铺垫，从而更好地实现∠A与∠BOC之间关系的探索。

设计意图：例题中的“问题串”将各个知识点进行有机融合，帮助学生理解抽象的知识点，并能引导学生从多个角度去解决问题。在此过程中，学生能够学会思考、分析，并有意识地发展自己的发散思维能力，遵循“逐步推进、螺旋上升、不断深化”的认识规律，使探究更具有操作性，能站在更高层次重新领悟所学知识，让学习变得更加主动、有效和持久。

二、发出思维的“芽”——条件改变

思维的“芽”是指在数学基本题型已经解决的基础上进行转化拓展，通过变换题目条件或结论，提出有梯度的问题，但梯度不大，让学生能运用原题型的思想方法，进行简单的转化，充分发挥学生的自主探究能力，激发学生解决此类数学题型的欲望，培养发散性思维能力。

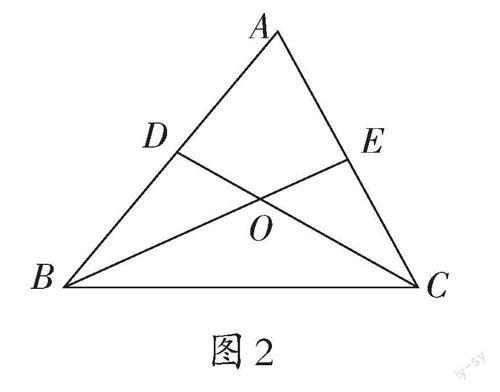
变式1 如图2，在△ABC中，（1）若∠ACB=70°，∠ACD=∠EBC，求∠BOC的度数；（2）若∠A=40°，∠ABC=∠ACB，∠ACD=∠EBC，求∠BOC的度数。

变式1中的问题（1）是在例题的第（1）（2）两问的基础上进行了主干条件的变化，在思维“种子”的启发下，利用转化与整体的思想方法催生思维的“芽”，促进问题解决；而问题（2）是在问题（1）基础上逆向转化成问题（1）的条件，再用整体思想去解决。本题通过变换题目的条件，由局部走向整体，将知识形成系统，提升学生思维的灵活性。

设计意图：数学学习是以思维活动为核心的学习。教师的“教”应建立在促进学生深度学习的基础上，让学生能够运用基本知识、基本技能解决数学问题。恰当的变式训练不仅能帮助学生巩固基础知识，及时反馈教学信息，还能激励学生积极参与，激发学生深入思考，使之创造力发挥出来，启迪学生智慧。

三、抽出思维的“枝”——图形变换

思维的“枝”是指枝干问题与主干问题相连，是从主干问题向外延伸的重要途径。主干与枝干相互联系、相互依托，形成一种内在思维的脉络，在图形变换中，可使学生思维向不同方向延伸、拓展。

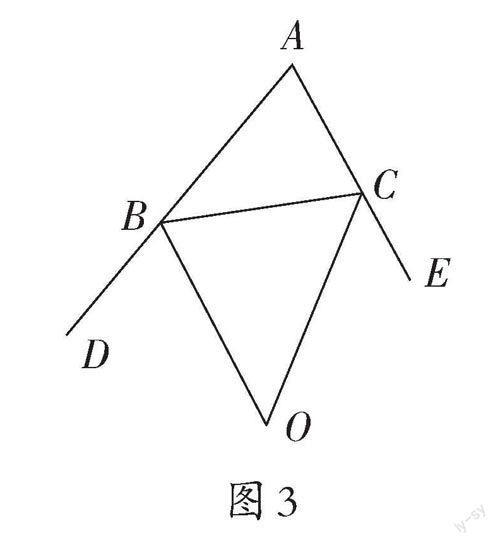
变式2 如图3，∠A=70°，BO、CO分别是△ABC外角∠CBD、∠BCE的角平分线，它们交于点O，求∠BOC的度数。

变式2在例题和变式1的基础上改变了图的形状，将已知条件中两个内角的角平分线转换为两个外角的角平分线，培养学生的识图能力，需要学生用转化的思想改变思考方式，横向提高学生发散思维能力。变式2沿用了探索最基础的知识和方法——用思维的“芽”来解决，从内角问题转化成外角问题，把主干问题向外延伸，抽出思维的“枝”，从而形成一种内在的思维脉络，最终实现∠A与∠BOC之间关系的探索，建立“两线两夹角”模型。

设计意图：变式2通过变图训练，设计一定“坡度”，提升学生发散性思维，帮助学生将解题视角由整体走向局部。这种从横向角度提出问题的方法，不仅对学生的解题能力有帮助，而且有利于培养学生思维的发散性。

四、长出思维的“树” ——探究发散

思维的“树”是整个枝干由内向外展開，深层次地引发学生思考与探究。学生思考的最大障碍是复杂问题，而思维的“树”则能把复杂问题简单化，通过分解与转化，改变研究方法，快速找出问题的关键，提高思维的发散性与归纳性，从而轻松地解决问题，呈现出完整的思维结构。

变式3 如图4，∠A=80°，BO、CO分别是△ABC

内角∠ABC及外角∠ACD的角平分线，它们交于点O。求∠BOC的度数。

变式3与前几题提出的问题探索、求解的方法有所不同，不再求∠OBC与∠OCB度数的和，而是用到前几题探讨出的结论，启发学生思考。此题利用三角形外角的性质及等式的性质进行变形，从而探索出∠OBC和∠OCB之间的关系，进而求出∠BOC的度数，推进∠A与∠BOC之间关系的探索，把“两线两夹角”模型进行了变形。

设计意图：本题通过对“两线两夹角”模型进行变形，改变了学生在解题时依葫芦画瓢的模式，帮助他们克服静止看问题的习惯，激发学生探究热情，改善了学生的思维方式，有利于提高学生发现问题、提出问题的意识和能力，培养学生思维的敏捷性和批判性。这种承上启下、由浅入深、由易到难、循序渐进的设计，恰到好处地调动了学生数学发散性思维的探究能力，让不同水平的学生都能得到一定发展，体会解题的乐趣。

五、开出思维的“花”——类比提升

类比思想是数学重要的解题思想，通过对题目反复锤炼、变式拓展、类比提升、精心整合，把创造性发散思维模式向学生最近发展区无限散发，思维的“花”定将绽放。

变式4 如图5，∠MON=90°，点A、B分别在OM、ON上运动（不与点O重合），BC是∠ABN的角平分线，BC的反向延长线交∠OAB的角平分线于点D。试问：随着点A、B的运动，∠D的大小会变吗？如果不会，求∠D的度数；如果会，请说明理由。

变式4从图的形状上看与变式3有所不同，甚至感觉没联系。但如果把图5顺时针转动到图6这个位置，并且延长线段AB，便会发现，此题其实就是变式3的演变。此题通过引导学生运用已有的知识经验，将复杂图形转化为简单的基本图形，体现基本图形在解决问题中的作用，巩固思维成果。

设计意图：变式4较变式3难度有所增加，将“两线两夹角”模型和旋转结合起来，再一次升华了“两线两夹角”模型，让学生明白此模型应用的广泛性，理清题目核心条件之间的联系，从而将整体性的结构图形投射到自己的认知中，在延伸中发现基本图形，提升自己的思维品质。这不仅体现在题目本身的开放性上，也体现了选题的指向性，提高学生学习能力。

（作者单位：江苏省徐州淮海国际港务区柳新镇中心中学）