基于切片耦合理论的斜齿轮时变啮合刚度分析
朱丽莎, 王奇斌, 栾晓刚, 袁 聪, 张义民
(1. 肇庆学院 机械与汽车工程学院,广东 肇庆 526061; 2. 西安电子科技大学 机电工程学院,西安 710071;3. 金象传动设备股份有限公司,江苏 淮安 223001; 4. 东北大学 机械工程与自动化学院,沈阳 110819)
斜齿轮系统广泛应用于航空航天、汽车、船舶等领域,其性能很大程度上决定了主机的性能、寿命、安全性、可靠性。时变啮合刚度是齿轮传动系统的重要内部激励,对齿轮系统的振动特性有很大的影响。因此,如何准确地计算齿轮系统时变啮合刚度特性是齿轮重要研究内容之一。
国内外学者们[1-3]针对齿轮时变啮合刚度特性做了大量的研究,主要研究方法有解析法、有限元法。有限元法能够准确地模拟齿轮实际情况且具有较高的计算精度,但通用有限元软件(ANSYS、ABAQUS等)针对不同的对象需要重复建模而且接触分析计算效率低等缺点。经多年研究,解析法取得了长足的发展和进步,广泛应用于齿轮系统时变啮合刚度特性分析。在解析法中,将齿轮等效为变截面悬臂梁,应用潜在能量法计算其刚度,其刚度包括轮齿弯曲刚度、剪切刚度、径向压缩刚度、接触刚度和齿基刚度[4-9]。另外,考虑摩擦、齿廓修形、裂纹、剥落等因素分析了齿轮系统的时变啮合刚度特性[10-19]。
以上研究多针对直齿轮系统,针对斜齿轮副通常使用切片理论将斜齿轮沿齿宽方向等效为若干直齿轮薄片,每个薄片直齿轮等效为直齿轮。Wang等[20]考虑斜齿轮齿廓误差基于切片理论建立了斜齿轮时变啮合特性模型,分析了斜齿轮时变啮合刚度、载荷分布、传递误差、应力分布等特性。Wan等[21]基于切片理论使用累积积分方法建立了斜齿轮时变啮合刚度模型,分析了裂纹、螺旋角、模数对时变啮合刚度的影响。在上述研究的基础上,Feng等[22]考虑齿基刚度修正、非线性接触刚度、齿面摩擦等因素分析了斜齿轮系统时变啮合刚度特性。但上述文献没有考虑轴向力对斜齿轮刚度特性的影响,Wang等[23]提出了考虑轴向变形的斜齿轮时变啮合刚度模型,分析轴向变形对时变啮合刚度的影响。但上述文献均没有考虑轮齿接触区域变形与非接触区域的耦合作用,而事实上轮齿非接触区域会抵抗接触区域的变形,增强了斜齿轮啮合刚度。
因此,本研究考虑切片之间的耦合作用,基于切片理论提出斜齿轮时变啮合刚度模型。首先将斜齿轮沿齿宽方向等效为若干切片,将切片耦合作用等效为弹簧模型,提出弹簧刚度模型。其次设计了一种数值求解法计算斜齿轮时变啮合刚度。最后以一对斜齿轮副为例,分别使用有限元法、切片耦合法、切片无耦合法对比分析斜齿轮时变啮合刚度。
1 时变啮合刚度模型
斜齿轮可以等效为一系列沿齿宽方向的薄片齿轮,每个薄片齿轮可被视为直齿轮,其中:B为斜齿轮宽度,Δl为切片厚度,bi为切片的轴向位置,如图1所示。

图1 斜齿轮切片模型Fig.1 Slice model of a helical gear
直齿轮刚度包括轮齿刚度和齿基刚度两部分。基于文献[24]中潜在能量法的研究,轮齿刚度包括弯曲刚度、剪切刚度、径向压缩刚度,如图2所示。这些刚度可以表示为
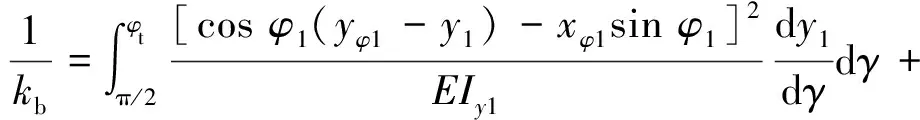
(1)
(2)
(3)
式中:yφ1为啮合点和原点之间的水平距离;E,G,v分别为材料的弹性模量、剪切模量和泊松比;y1和y2分别为过渡曲线和渐开线上积分点的水平坐标;Iy1,Ay1,Iy2,Ay2为过渡曲线和渐开线上任意位置处的截面惯性矩和横截面积,其他参数见图2。

图2 轮齿刚度模型Fig.2 Stiffness model of a tooth
轮齿的刚度包括轮齿弯曲刚度、轮齿剪切刚度和径向压缩刚度,各切片轮齿的刚度可表示为
(4)
轮齿副在啮合过程中还会产生接触变形,基于赫兹接触理论,赫兹接触刚度可表示为
(5)
在外力的作用下,不仅产生轮齿变形,而齿基也会发生变形,因此,齿基刚度也是齿轮啮合刚度的一部分,Sainsot等提出了齿基刚度计算模型,其表达式为
(6)
式中:uf和Sf如图3所示; 系数L*,M*,P*和Q*可按照式(7)的多项式函数计算得到。

(7)
式中:X*为系数L*,M*,P*和Q*;hf=rf/rint,rf,rint和θf见图3;Ai,Bi,Ci,Di,Ei和Fi的值如表1所示。

图3 齿轮齿基变形几何参数Fig.3 Geometrical parameters for the gear-foundation stiffness
上述齿基刚度计算法适用于单对轮齿啮合时。当多对轮齿同时处于啮合状态时,单纯的多对齿基刚度相加使齿轮啮合刚度计算结果误差较大,Ma等[25]基于式(6)提出了改进的多齿啮合齿基刚度计算方法,可表示为
(8)
式中:λ为齿基刚度修正因子,当齿轮处于单齿啮合时,λ=1,当齿轮处于多齿啮合时,λ可以通过有限元方法计算得到;kfp和kfg分别为主动齿轮和从动齿轮在单齿啮合区域的齿基刚度,可由式(6)得出。

表1 多项式系数表Tab.1 Coefficients of the polynomial function
2 切片耦合理论
如图4所示,图4中黑色实线为斜齿轮接触线,斜齿轮啮合过程是从主动齿轮一个端面的齿根处和从动齿轮的齿顶处开始,之后接触线由短变长,再由长变短,最后在主动齿轮另一端面的齿顶处和从动齿轮的齿根处全齿分离。从图4可知,斜齿轮啮合过程中会出现部分切片轮齿啮合,部分切片轮齿分离的状态。处于啮合的切片轮齿在啮合力的作用下产生啮合变形,而处于分离的切片轮齿由于力的传递作用也会产生变形,本研究定义该变形的传递作用为切片耦合。
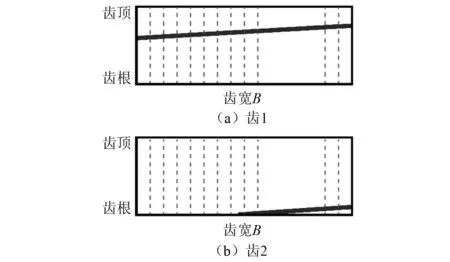
图4 斜齿轮接触线Fig.4 Contact line of the helical gear pair
考虑切片耦合作用,建立轮齿的啮合刚度模型如图5所示。从图5可知,轮齿可以等效为多个切片,其中每个切片可等效为一个弹簧。基于文献[26]的研究,切片轮齿的弯曲变形、剪切变形、径向压缩变形会传递给相邻的切片轮齿,而接触变形对相邻齿的影响可以忽略。所以每个弹簧的刚度为切片轮齿的刚度kt,包括轮齿弯曲刚度、剪切刚度和径向压缩刚度。切片轮齿的耦合效应可等效为图5中的弹簧模型,其刚度可以表示为
(9)
式中:Cc为切片耦合因子,对于斜齿轮该值等于1;m为斜齿轮模数。
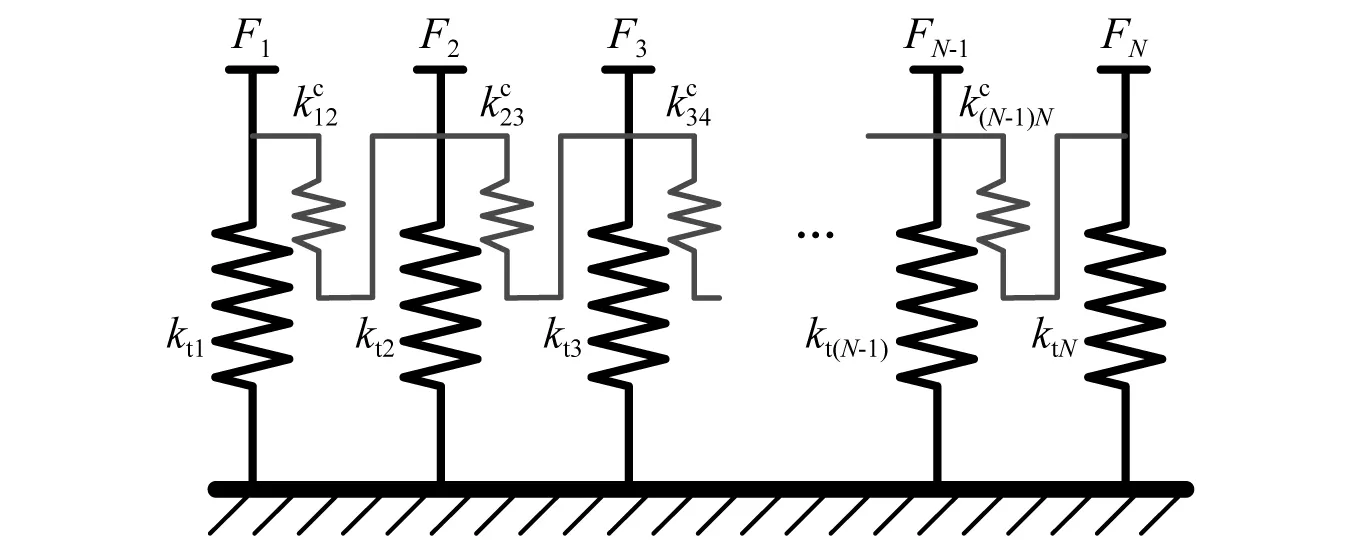
图5 斜齿轮切片耦合模型Fig.5 Coupled slice model of the helical gear
各弹簧在啮合力Fi的作用下产生啮合变形δti,其可表示为
(10)
齿轮啮合的总啮合力等于各切片啮合力之和,可表示为
(11)
处于啮合中的各切片变形为δti,而未处于啮合的切片轮齿也会产生啮合变形,其变形等于相邻切片的变形乘以变形传递系数,可表示为
δt(i+1)=Γi(i+1)δti
(12)
式中:δti为相邻处于啮合切片的变形; Гi(i+1)为变形传递系数,可表示为
Γi(i+1)=
(13)
上述理论适用于单个齿轮在外力作用下的啮合变形,对于处于啮合中的一对轮齿,它们的变形如图6所示。图6中:kpi,kgi,khi分别为主动轮齿刚度、从动轮齿刚度和接触刚度;δpi,δgi,δhi分别为其变形量;Fi为啮合力;δi为啮合变形。 它们之间的变形及力平衡方程为
δpi+δgi+δhi=δi
(14)
kpiδpi=kgiδgi=khiδhi=Fi
(15)
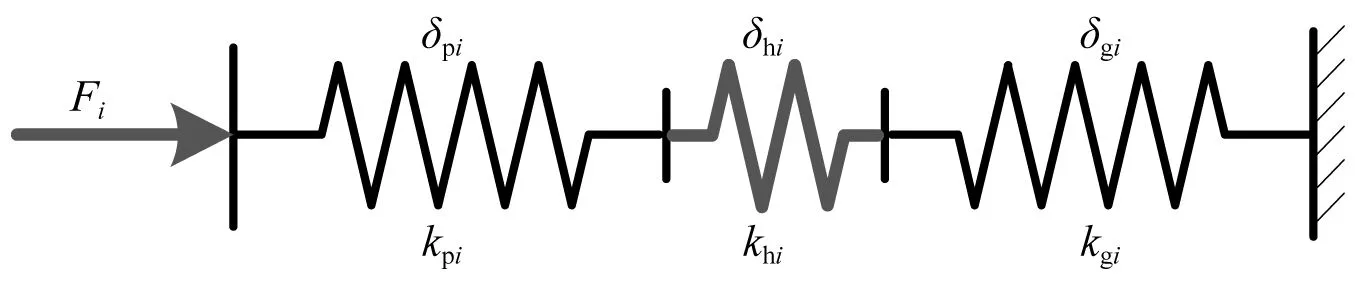
图6 主动齿轮、从动齿轮、接触变形关系Fig.6 The deformation relationship among the driving gear, driven gear and their contact
那么齿轮副啮合变形δi以式(16)表示,即通过求解主动齿轮的变形即可得到啮合齿轮副的变形。
(16)
齿轮系统的轮齿刚度可通过式(17)计算
(17)
齿基刚度和轮齿刚度为弹簧的串联形式,考虑齿基刚度,斜齿轮系统的啮合刚度为
(18)
3 求解流程
在式(10)中,由于各切片轮齿变形的不同,所以轮齿变形不能直接求得,因此,本文采用数值方法对各弹簧变形进行计算,计算流程如图7所示。
步骤1输出齿轮系统基本参数,包括齿轮参数、材料参数和载荷参数;
步骤2确定齿轮初始啮合位置,将齿轮沿齿宽方向进行切片,根据Wang等的方法确定各切片啮合状态,计算各切片轮齿刚度、切片耦合刚度和齿基刚度,并通过有限元模型确定齿基刚度修正因子;
步骤3令轮齿初始啮合变形为δ,进一步确定啮合状态、非啮合状态各主动齿轮切片轮齿啮合变形δpi;
步骤4根据式(10)计算各切片啮合力Fi、齿轮啮合力Fm,比较齿轮啮合力Fm与外载荷F,若|F-Fm|>Fε,设置一个新的啮合变形δ,重复步骤3;若|F-Fm|≤Fε,即可得到载荷F下齿轮啮合变形δ;其中Fε为迭代计算的预给精度,本文中取1。
步骤5计算轮齿啮合刚度ktt,进一步考虑齿基刚度ktf,计算齿轮副啮合刚度k;
步骤6在下一个啮合位置重复上述过程直到完成一个啮合周期的仿真,即可得到斜齿轮系统时变啮合刚度。
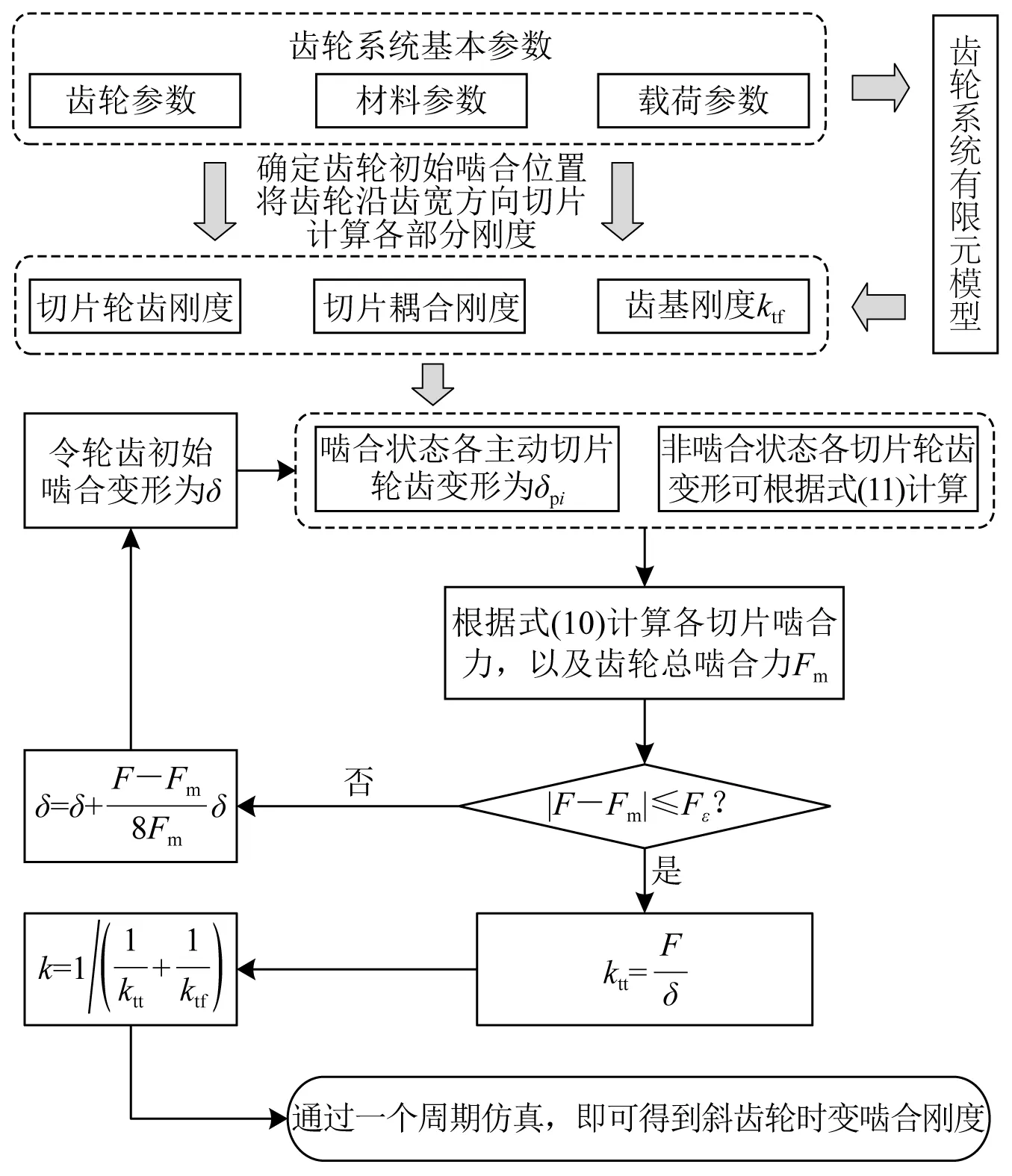
图7 切片耦合方法计算流程Fig.7 The simulation flow of coupled slice theory
4 结果与讨论
本章以表2中的斜齿轮副为例,建立斜齿轮副有限元模型对当前模型进行验证,并通过分析考虑切片耦合的斜齿轮时变啮合刚度和不考虑切片耦合的时变啮合刚度确定当前模型的先进性和有效性。
考虑斜齿轮切片耦合,运用本文方法建立斜齿轮副时变啮合刚度模型,将齿轮沿齿宽方向等效为直齿轮切片(本文中切片数为50),计算各切片轮齿刚度、切片耦合刚度和齿基刚度,其中切片耦合因子Cc=1,齿基刚度修正因子λ=1.09,通过一个周期50个点的仿真,得到斜齿轮时变啮合刚度如图8中黑色实线所示。在不考虑切片耦合时,令切片耦合因子Cc=0,其他参数均与考虑切片耦合时相同,计算斜齿轮时变啮合刚度如图中带圈实线所示。

表2 斜齿轮参数Tab.2 Parameters of the helical gear pair

图8 斜齿轮时变啮合刚度Fig.8 Time-varying mesh stiffness of helical gear pair
基于表2中的斜齿轮参数,采用有限元分析软件ANSYS建立斜齿轮系统有限元模型,如图9所示。图9中齿轮采用Solid185单元,并对齿轮表面做了表面细化,齿轮啮合采用Conta173和Targe170单元。齿轮轴孔表面通过刚性连接到齿轮中心点,主动齿轮除绕齿轮方向的旋转自由度外,中心点其他自由度均约束;从动齿轮中心点各自由度均约束,在主动齿轮旋转方向施加外载荷扭矩,通过有限元接触分析即可得到该时刻斜齿轮的时变啮合刚度,将一个啮合周期分割成20个点进行仿真即可得到斜齿轮时变啮合刚度(见图8中虚线)。

图9 斜齿轮有限元模型Fig.9 Finite element model of helical gear pair
在本研究中,将斜齿轮啮合区域分为单齿啮合区和双齿啮合区,双齿啮合区由过渡区和完全双齿啮合区组成。齿轮时变啮合刚度对比,如表3所示。考虑切片耦合的斜齿轮时变啮合刚度计算方法与有限元方法在单齿啮合区、双齿过渡区和完全双齿区趋势完全一致,最大相对误差分别为0.5%,0.7%,0.6%。切片无耦合方法与有限元法、切片耦合方法相比,在单齿啮合区和完全双齿区结果基本一致,相比有限元法,最大相对误差分别为0.2%,0.5%,但在双齿过渡区,切片无耦合方法刚度均小于其他两种方法,最大相对误差为2.0%,主要因为在双齿过渡区域,轮齿沿齿宽方向处于局部接触状态,切片无耦合方法不能考虑局部非接触状态的切片轮齿对局部接触状态切片轮齿刚度的增强作用。而切片耦合方法能够考虑处于不同接触状态切片轮齿的耦合作用,更准确地模拟轮齿的变形,所以结果更加精确。综上所示,切片耦合方法能够准确地模拟斜齿轮的啮合特性。
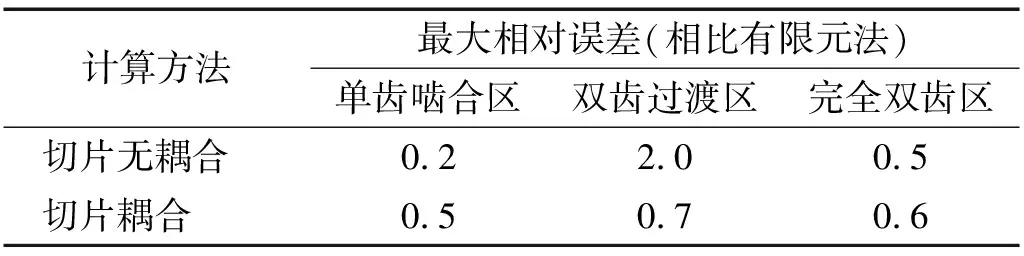
表3 齿轮时变啮合刚度对比Tab.3 Comparison of time varying meshing stiffness %
同时,本文还对比分析了不同齿数、模数、齿宽的斜齿轮案例,由于版面限制没有一一列举,结果表明切片耦合方法同样有效,且具有普适性。
另外,我们分析了不同切片数下(N=10,N=25,N=50,N=75,N=100)斜齿轮时变啮合刚度,结果如图10所示。从图10可知,当N=10和N=25时,图中刚度曲线有一些凸起,主要是因为切片数较小时,每个切片的厚度较大,随着齿轮的旋转,每个切片进入啮合和退出啮合都会使总刚度产生大的变化,进行形成凸起。当N=50,N=75,N=100,刚度曲线已较平滑,为减少计算量,本研究中N=50即可。
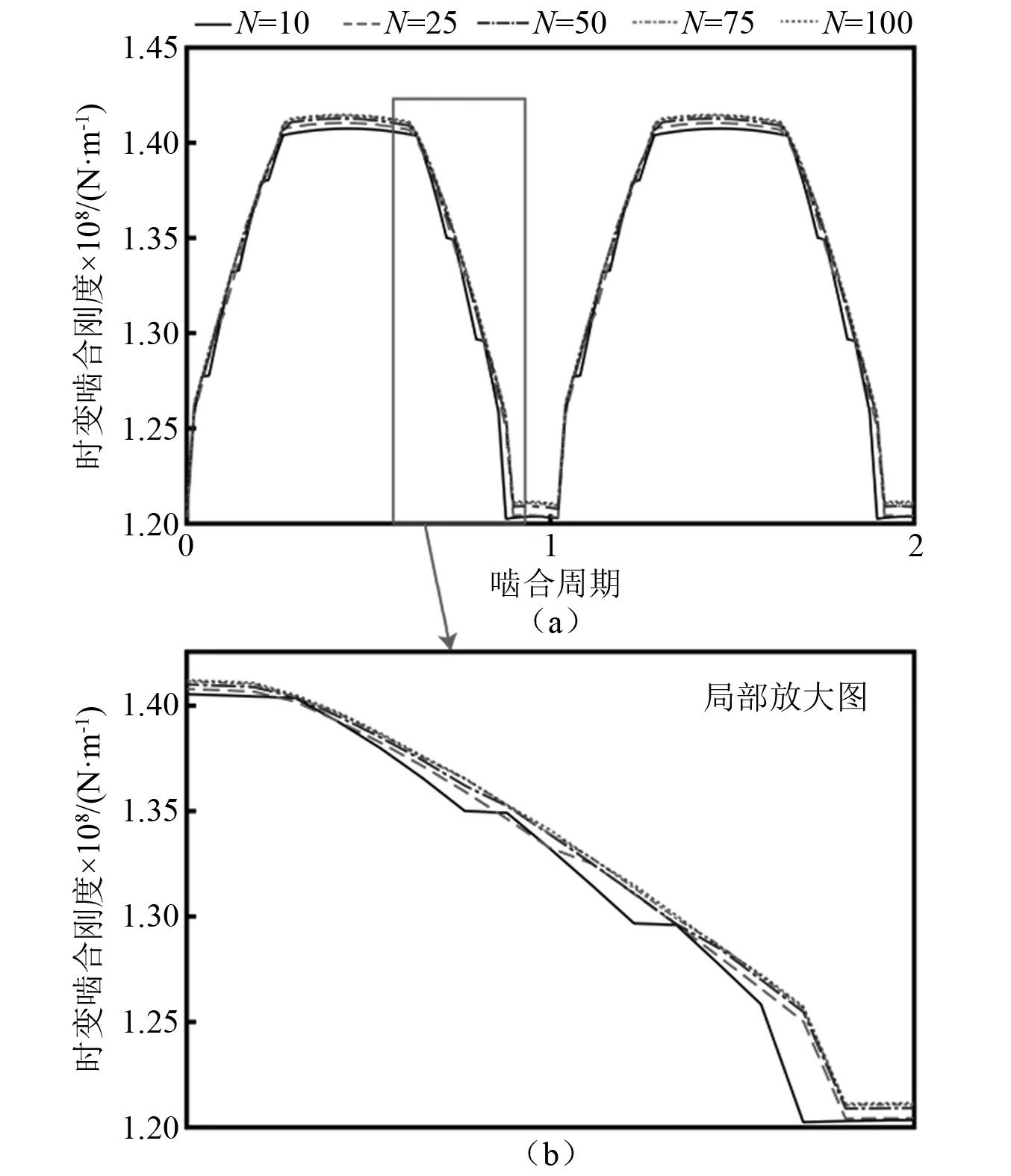
图10 不同切片数斜齿轮时变啮合刚度Fig.10 Time-varying mesh stiffness of helical gear pair under different number of slice teeth
5 结 论
(1) 针对斜齿轮时变啮合刚度精确求解问题,本研究提出基于切片思想及切片耦合理论的斜齿轮啮合刚度计算方法。将齿轮沿齿宽方向等效为若干切片直齿轮,各切片直齿轮的刚度采用潜在能量法计算。将切片耦合作用等效为弹簧模型,提出了其刚度模型,其变形等于相邻两个切片的变形差。最后,设计了一种数值求解模型计算斜齿轮时变啮合刚度。
(2) 建立了斜齿轮有限元模型,对比分析了切片无耦合、切片耦合下斜齿轮时变啮合刚度特性,结果显示切片耦合斜齿轮时变啮合刚度模型能够在单齿啮合区、双齿过渡区、完全双齿区准确地模拟仿真斜齿轮时变啮合刚度特性,切片无耦合斜齿轮时变啮合刚度模型在单齿啮合区、完全双齿区能够准确地计算斜齿轮啮合刚度,但在过渡区,由于没有考虑切片轮齿非接触区域与轮齿接触区域的耦合作用,所以不能准确地模拟斜齿轮啮合刚度。

