热环境下功能梯度环板的谱几何法自由振动解
石先杰, 左 朋,2
(1. 中国工程物理研究院 总体工程研究所,四川 绵阳 621999;2. 中国科学技术大学 近代力学系,合肥 230026)
功能梯度材料[1-3]作为一种新兴材料,它克服了传统材料在过热环境下机械性能下降的缺陷,具有极强的耐热性,而由其所制成的环板结构有着质量轻、结构刚度大、力学性能好、承载能力强等优点,在航空航天工程、飞机工程、核反应堆等领域的发动机端盖上有着广泛应用。因此,这类结构在实际工程应用中通常会受到复杂工作环境的影响而产生较大的振动甚至引起疲劳损伤。因此,准确分析预测功能梯度环板结构振动特性一直是国内外专家学者的研究热点。为此,国内外学者已开展了一系列数值求解方法研究,如Rayleigh-Ritz法[4-6]、微分求积法[7-10]、拟格林函数法[11]和有限环形棱柱法[12]等。
然而,上述研究均是基于常温环境,在高温环境下,结构的材料属性会随着温度的变化而改变,从而导致其自由振动的固有频率相比于常温下变得明显不同。对于热环境下功能梯度结构的振动特性,国内外学者进行了一些研究分析。假设材料特性依赖于温度,并在板的厚度方向上逐渐变化,Haddadpour等[13]采用伽辽金法求解运动方程,对简支功能梯度圆柱壳在热环境中的自由振动特性进行了分析。Mirtalaie[14]根据微分求积法,求解了热环境下功能梯度薄环形扇形板自由振动频率。在三维弹性理论的框架下,Yang等[15]分析了功能梯度环板的热振响应。在一阶剪切变形理论的框架内应用微分求积法,Malekzadeh等[16-17]研究了旋转功能梯度圆柱壳和带有弹性支撑的功能梯度环板在热场中的自由振动特性。用傅里叶级数结合辅助函数来描述板的位移容许函数,Zhou等[18]研究了弹性地基上具有温度梯度的超音速多孔功能梯度材料板的振动和颤振特性。Li等[19]采用特征正交多项式详细研究了功能梯度多孔阶梯圆柱壳在热场中的自由振动、稳态和瞬态响应特性。蒲育等[20-21]根据二维弹性理论,采用微分求积法分析了材料属性径向变化的功能梯度薄环板在热环境下的面内自由振动特性。同样是考虑材料属性沿径向变化功能梯度薄环板,吕朋等[22]采用改进傅里叶级数建立了其在热场中受弹性约束的面内振动分析模型。而对于沿厚度方向变化的功能梯度环板,石鹏等[23]应用三维Chebyshev-Ritz法对其在热环境下的自由振动特性进行了求解。
综上所述,目前关于功能梯度环板在热场中的自由振动分析虽然有一定的研究成果,但大部分研究工作集中在材料属性沿径向变化的薄环板面内振动问题。而对于厚环板问题,往往是采用三维弹性理论求解,存在着计算效率低等问题。因此,针对工程中更为常见的中厚环板,考虑材料特性沿厚度方向的梯度变化,本文以一阶剪切变形理论为基础,通过沿边界设置具有可变刚度的边界约束弹簧的方式来考虑任意边界约束。同时,采用谱几何法建立功能梯度环板热振分析模型。在谱几何法求解框架下,板的位移函数总是表示为标准的傅里叶余弦级数,并辅以四个正弦函数项来消除边界处位移函数的导数不连续性问题。这种级数展开方法理论上能够表征任意有限长结构的位移变量,且函数形式统一,易于参数化分析。在数值算例中,通过与文献解、有限元解的对比研究,验证了该模型的正确性,进而分析了边界条件、环境温度、梯度指数等对功能梯度环板固有频率的影响。
1 理论方法
1.1 模型描述
考虑如图1所示的功能梯度环板,圆柱坐标系(r,θ,z)位于结构的几何中面上。图1中:R0和R1分别为环板沿径向方向r的内径和外径;θ为圆周方向;h为环板的厚度。文中研究的功能梯度材料由陶瓷和金属材料两种成分组成,其有效材料参数P(包括弹性模量E、密度ρ、泊松比ν和热膨胀系数α等)沿环板厚度方向呈梯度变化,可以被描述为[24]
(1)
式中:Pt和Pu分别为环板上、下表面的材料参数;-h/2≤z≤h/2;p为功能梯度指数。考虑热环境的影响,功能梯度材料的有效材料参数Pξ(ξ=t,u)在温度值T的变化影响下有着如式(2)所示的性质
Pξ(z,T)=P0ξ(P-1ξT-1+1+P1ξT+P2ξT2+P3ξT3)
(2)
式中,P-1ξ,P0ξ,P1ξ,P2ξ和P3ξ为温度相关系数。文中研究的是均匀温度分布的情形[25],T0为参考温度,其温度变化为ΔT=T-T0。

图1 功能梯度环板的几何形状以及坐标系Fig.1 Geometric shape and coordinate system of functionally graded annular plate
1.2 能量方程
根据一阶剪切变形理论,环板上任一点沿r,θ和z方向的位移场分量u,v,w的表达式可以写成
u(r,θ,z,t)=u0(r,θ,t)+zφr(r,θ,t),
v(r,θ,z,t)=v0(r,θ,t)+zφθ(r,θ,t),
w(r,θ,z,t)=w0(r,θ,t)
(3)
式中:u0,v0,w0分别为环板在几何中面上沿r,θ和z方向的位移分量;φr和φθ分别为在rz和θz平面上的转角位移分量。
根据中厚板理论,环板结构中的应变和位移之间存在线性关系式
(4)

(5)
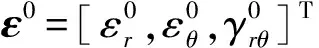
ε=[εr,εθ,γrθ,γrz,γθz]T,
σ=[σr,σθ,τrθ,τrz,τθz]T,
σ=Q(5×5)ε
(6)
式中,Q(5×5)为与温度值T和厚度坐标z有关的弹性常数所组成的矩阵(参考2011年Malekzadeh等的研究),其元素的具体值为
(7)
对应力分量σ在z方向积分,引入剪切修正系数κ=5/6, 得到环板的本构方程表达式
N=Aε0+Bχ,M=Bε0+Dχ,Qκ=Aκγ
(8)
式中:N=[Nr,Nθ,Nrθ]T和Q=[Qr,Qθ]T分别为环板的合力和横向剪应力分量;M=[Mr,Mθ,Mrθ]T为合弯矩分量;A(Aκ),B和D分别为以结构的拉伸刚度、拉伸-弯曲耦合刚度和弯曲刚度为元素组成的矩阵,其具体表达式可见2011年Malekzadeh等的研究。
根据建立的本构方程表达式,结合2011年Malekzadeh等给出的热应力描述,得到环板的应变能表达式

(9)
代入位移场分量可以得到环板的动能表达式
(10)
文中通过在环板的内部和外部放置边界弹簧实现边界条件的模拟。边界约束弹簧所储存的能量可以写成
(11)
式中,上标0和1分别为设置在环板内部和外部的边界弹簧刚度值。
1.3 位移容许函数以及方程的求解
文中分别采用了谱几何法和傅里叶正余弦函数来表示环板沿径向方向和周向方向的位移容许函数
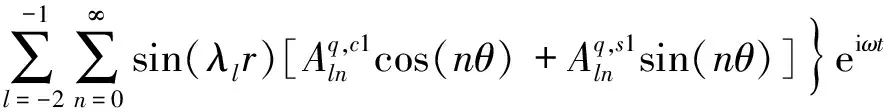
(12)
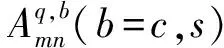
如上所述,热环境下功能梯度环板的拉格朗日能量泛函可以写成
(13)
根据1.2节的能量方程表达式,结合相应的位移容许函数进行求解,并采用Rayleigh-Ritz法对未知展开系数求偏导,可以得到热环境下功能梯度环板自由振动特征方程
(K-ω2M)H=0
(14)
式中:K和M分别为环板的刚度矩阵和质量矩阵;H为未知系数向量,其中温度变化会影响K。
2 数值算例与分析
根据上述分析获得的自由振动特征方程,本章将分析热环境下功能梯度环板自由振动特性。根据航空航天飞行器的工程实际应用,在接下来的数值算例中选择了几何尺寸为R0=0.5 m,R1=2.0 m,h=0.10 m的环板结构作为研究对象。通过设置边界约束弹簧的刚度值,文中研究考虑了包括经典和弹性边界在内的10种任意边界条件,并且采用了不同字母来表示,其中: C,SS,SD和F分别为固支、简支、剪切-膜片边界和自由边界; E1,E2,E3,E4,E5和E6为弹性边界。它们的弹簧刚度值按Su等的研究设置。此外,位移容许函数在径向和周向方向的级数在理论上可以展开为无穷项。但是考虑到实际数值计算需要,文中对其截断至有限项。参考文献[26]对谱几何法收敛性分析结果,文中研究将径向和周向的级数均截断为M=N=14。
2.1 数值验证
不同边界条件和梯度指数p下功能梯度环板在不考虑热环境影响情况下的第1阶固有频率,如表1所示。算例包括了两种板的厚度h=0.05 m和h=0.10 m, 其余几何尺寸与默认参数保持一致。环板的上、下表面材料分别为铝和氧化锆,材料参数为:Et=168 GPa,νt=0.3,ρt=5 700 kg/m3,Eu=70 GPa,νu=0.3,ρu=2 707 kg/m3。表1中将谱几何法模型计算结果与Su等的研究结果进行了对比。从表1可以看出,文中结果与Su等的解非常接近,存在的偏差主要来源于径向所采用的位移函数差异。这表明文中模型边界约束弹簧刚度以及截断数的设置是合理的,可以有效求解具有不同梯度指数p的功能梯度环板的自由振动特性。
在开展热环境下功能梯度环板结构自由振动分析时,由于缺乏相关文献数据作为参考。因此,文中采用有限元法(finite element method,FEM)计算结果作为对比数据。环板上、下表面的材料分别为氮化硅(Si3N4)和304不锈钢(SUS304),它们在热场中的材料参数如表2所示。环板的几何尺寸与默认参数保持一致,参考温度取为T0=300 K。同样是考虑了C-C,SS-SS和C-SS三种经典边界条件。不同温度变化ΔT下环板前5阶固有频率对比情况(梯度指数p=1.0),如表3所示。不同梯度指数p下的前9阶固有频率对比(温度变化ΔT=150 K),如表4所示。两种方法得到的频率结果可以较好地匹配,最大偏差在0.8%以内。偏差的来源主要是文中方法和FEM分别采用了不同的板壳理论和求解方法体系。此外,FEM计算结果的求解精度依赖于网格密度,需要不断地细化网格才能获得更加准确的结果,但同时也会带来计算成本的增加。两种方法求解获得的模态振型对比情况,如图2所示。其中温度变化ΔT=150 K, 梯度指数p=0.5, 边界条件为C-C。从图2可以看出,基于两种方法获得的模态振型一致性较好。综上所述,文中方法可以有效地分析热环境下功能梯度环板自由振动特性。

表1 具有不同边界条件和梯度指数的功能梯度环板的第1阶固有频率Tab.1 The first natural frequency of functionally graded annular plate with different boundary conditions and gradient indexes
2.2 参数化分析
在验证文中构建模型准确性和通用性的基础上,针对航空航天飞行器工程运用中的各种复杂工况,本节对功能梯度环板在热环境下的振动特性开展参数化分析。结构的几何尺寸以及材料的选择与表3、表4保持一致。
首先,当温度变化ΔT=50 K时,各种复杂边界条件下功能梯度环板固有频率,如表5所示,材料梯度指数p=1。从表5可以看出,对于经典边界,C-SD边界下的固有频率最高,SS-SD和SD-SD边界下的频率结果非常接近,而F边界的存在会很明显地降低结构的固有频率。而对于弹性边界,在E1-E1和E4-E4边界条下环板分别有着最高和最低的固有频率。
温度变化ΔT对功能梯度环板固有频率(n=1,m=1)的影响情况,如图3所示。图3中,材料的梯度指数p=1。不难看出,在经典、经典-弹性以及弹性边界条件下,随着ΔT增大,环板的固有频率会不断降低。这是因为ΔT变大降低应变能导致了功能梯度环板刚度降低,从而使结构固有频率减小。
梯度指数p以及周向波数n的变化对环板固有频率的影响,如图4所示,温度变化ΔT=50 K。从图4可以发现,结构固有频率会随着周向波数n的增加而不断增加。而随着梯度指数p的增加,功能梯度环板的固有频率先是迅速下降,达到一定值后,影响逐渐不明显。因为随着p的增加,环板材料属性更加接近于下表面的金属组分,从而降低了结构的固有频率。

图4 周向波数n和梯度指数的变化对功能梯度环板固有频率的影响Fig.4 The influence of changes in circumferential wavenumber n and gradient indexes on the natural frequencies of functionally graded annular plates
3 结 论
综合考虑功能梯度环板材料属性温度相关性及其在厚度方向上梯度连续变化,本文在一阶剪切变形理论框架下推导出功能梯度环板振动能量方程,并采用谱几何法求解得到功能梯度环板在热场中的自由振动特性。通过将文中计算结果与相关文献和有限元法结果进行对比,验证了所构建分析模型的正确性和可靠性。在此基础上,研究了边界约束条件、温度变化和梯度指数等参数对热环境下功能梯度环板自由振动特性的影响,获得以下结论:
(1) 文中所构建的计算分析模型可以有效分析预示热环境下功能梯度环板自由振动特性。
(2) 对于经典边界,SS和SD边界对功能梯度环板自由振动固有频率的影响类似,F边界则会很明显地降低结构固有频率。对于弹性边界,E1和E4边界下的功能梯度环板分别有着最高和最低的固有频率。
(3) 功能梯度环板固有频率随着温度变化ΔT的增加而降低;而梯度指数p的增加,则会导致功能梯度环板的固有频率呈现先迅速下降后逐渐稳定的趋势。

