非局部功能梯度梁结构振动与波传播特性研究

何东泽， 史冬岩， 王青山， 马春龙,4

(1. 哈尔滨工程大学 机电工程学院，哈尔滨 150001； 2. 中南大学 机电工程学院，长沙 410083；3. 中南大学 高性能复杂制造国家重点实验室，长沙 410083； 4. 哈尔滨职业技术学院 汽车学院，哈尔滨 150001)

随着众多科研人员对纳米材料的研究探索，微纳米电子机械系统的设计开发的研究逐渐深入。纳米梁结构作为具有良好力学性能的工程结构，其结构简单，在纳米线、微型开关以及微型驱动器等中作为基本的微小型元器件被广泛应用[1]。纳米结构的振动特性研究对于微纳米电子机械系统有着重要的工程意义，对纳米传感器以及某些纳米机械器件的设计具有广泛的应用背景。同时，纳米结构波传播的特性也是较为热点的研究问题。对于纳米结构的力学理论，目前主要包括修正耦合理论[2-3]、应变梯度理论[4]以及非局部理论[5-6]。其中，非局部理论是目前微纳米结构以及微纳米电子机械系统应用研究中应用最广泛的理论。

目前对于微纳米梁结构的研究具有较大的进展，存在较多研究成果。主要包括：Li等[7]开展承受轴向张力以及轴向压缩力作用下非局部纳米梁的横向振动研究，对其固有频率，稳态响应以及稳定性进行分析研究；Li等[8]基于非局部应变梯度理论，采用广义微分求解法对轴向功能梯度纳米梁进行研究，分析其弯曲、屈曲及振动相关问题；张大鹏等[9]基于非局部黏弹性理论，采用传递函数法开展黏弹性地基上欧拉梁的自由振动分析研究；刘灿昌等[10]对考虑非局部效应和轴向非线性伸长下的欧拉纳米梁模型进行建立，分析非局部相应对梁模型固有频率的影响。

波传播问题是目前一个重点研究问题，国内外众多学者对其进行了研究并取得了丰硕的成果。Narendar等[11]根据欧拉-伯努利梁理论，结合非局部弹性理论，对梁结构中非局部参数与逃逸频率之间的关系进行了研究；王碧蓉等[12]基于非局部弹性理论与铁摩辛科梁理论，对应力梯度和应变梯度修正的梁模型进行研究，证明非局部因子对弯曲波频散特性有着一定的影响；余阳等[13]基于流体滑移边界理论，将非局部理论与应变梯度理论结合，建立充流单壁碳纳米管结构分析模型，对非局部效应、应变梯度效应以及流体滑移边界效应进行分析研究；Li等[14]结合非局部弹性理论以及欧拉伯努利梁理论，对磁场条件下的单壁层的碳纳米管结构的波传播特性进行分析研究。

本文基于非局部弹性理论，给出非局部功能梯度铁摩辛科梁的控制微分方程。结合本文提出的半解析求解方法，建立非局部功能梯度梁的数值分析模型。同时，开展非局部参数以及功能梯度指数对非局部功能梯度梁的自由振动特性以及波传播特性进行研究，比较分析频率参数、波传播频率以及波传播速度的变化情况，得出各个参数对非局部功能梯度梁的振动特性以及波传播特性的影响规律。

1 非局部理论与功能梯度材料

非局部理论是目前微纳米结构中应用较为广泛的一种理论。该理论认为，任意一点的应力不只与该点的应变有关，而是与总体结构的应变状态迭加之和相关。和传统的弹性理论理论不同，非局部理论考虑某点对某个作用区域的影响。Eringen[15]将传统的积分型本构关系转化为微分型本构关系，可以直接应用于控制方程之中。非局部本构关系方程可以表示为

(1)

式中：E为弹性模量；G为剪切模量；σxx为轴向正应力；σxz为剪应力；εxx为轴向应变；γxz为剪切应变； (e0a)2为非局部参数，e0为材料参数，a为非局部空间大小的材料内部的特征长度，当e0a趋于无穷大时，非局部理论将会近似于晶格理论。

功能梯度材料为两种或多种材料复合而成，是一种新型的复合材料。对于一维梁结构，定义其体积分数函数V为

(2)

式中：p为功能梯度指数，决定梁结构在厚度方向上的材料变化趋势；h为梁的厚度。因此，可以定义功能梯度梁结构的弹性模量E(z)，剪切模量G(z)以及体密度ρ(z)为

E(z)=(E1-E2)V+E2,
G(z)=(G1-G2)V+G2,
ρ(z)=(ρ1-ρ2)V+ρ2

(3)

式中， 下标1和2分别为材料1(钢)和材料2(氧化铝)的物理参数。

2 模型建立

本文所建立的非局部功能梯度纳米梁结构，如图1所示。图1中：L为梁的长度；h为梁的厚度；b为梁的宽度。定义梁的轴向方向为x轴方向，厚度方向为z轴方向。

图1 功能梯度纳米梁结构示意图Fig.1 Schematic diagram of FGM nanobeam

功能梯度纳米梁由钢(上表面)和氧化铝(下表面)组成，其材料参数如表1所示。

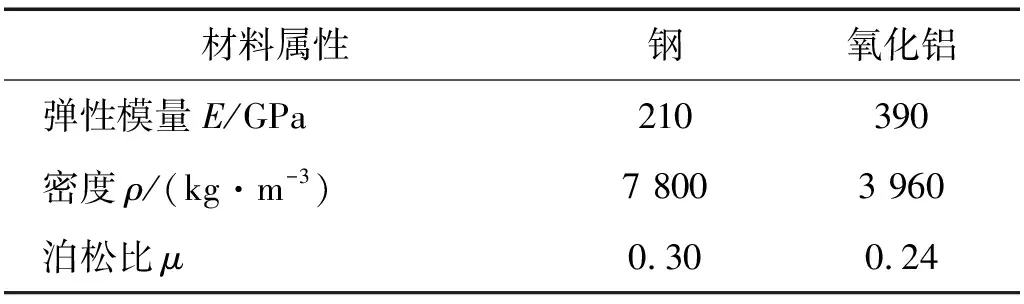
表1 功能梯度组成材料属性Tab.1 The material properties of FGM constituents

3 数值模型建立

根据铁摩辛科梁理论，任意一点的轴向位移u(x,z,t)以及横向位移w(x,z,t)可以表示为[16]

u(x,z,t)=u0(x,t)+zθ(x,t),
w(x,z,t)=w0(x,t)

(4)

式中：u0(x,t)，w0(x,t)分别为梁结构中性轴上任意一点的轴向位移与横向位移；θ(x,t)为梁横截面中性轴上任意一点的旋转位移。相应的应变可以表示为

(5)

相应的，对轴向力N、剪力Q以及弯矩M进行定义，可以表示为

(6)

根据非局部本构关系，结合式(6)，可以得到非局部广义力为

(7)

根据哈密尔顿原理，可得铁摩辛科梁的平衡方程为[17]

(8)

式中，I1，I2，I3为惯性质量，定义为

(9)

根据非局部关系，结合式(8)，可得非局部轴向力N、剪力Q以及弯矩M的表达式为

(10)

式中，Ks为剪切修正系数。将非局部轴向力N，剪力Q以及弯矩M代入式(8)中，可得

(11)

将位移变量量u0(x,t)，w0(x,t)以及旋转变量θ(x,t)转化为波动解，具体表示为[18]

u0(x,t)=U0eikxe-iωt,
w0(x,t)=W0eikxe-iωt,
θ0(x,t)=Φ0eikxe-iωt

(12)

式中：U0，W0，Φ0为位移以及转角幅值变量；k为轴向波数；ω为角速度；t为时间变量。将位移变量以及旋转变量代入式(11)，得

(13)

式中，各个变量的具体表达式见附录。为了保证系数存在非零解，其行列式必为零，可以得到关于k的六次多项式方程，为

a6k6+a4k4+a2k2+a0=0

(14)

式中，a0,2,4,6为相应的多项式系数，由式(13)决定。根据多项式方程的特征根，将位移变量以及旋转变量进行转化，表示为

(15)

式中，ns为轴向波的个数，具体数值由式(14)决定。将位移变量以及旋转变量继续变化，可以得到

(16)

式中，ξi，ηi为位移变量的比例参数，具体可定义为

(17)

式中，ki为式(14)的特征根。根据铁摩辛科梁理论，对边界条件进行分析。本文主要考虑简支、固支以及自由边界条件，具体定义为[19]：

自由边界条件

N(x,t)=Q(x,t)=M(x,t)=0

(18)

简支边界条件

N(x,t)=w0(x,t)=M(x,t)=0

(19)

固支边界条件

u0(x,t)=w0(x,t)=θ0(x,t)=0

(20)

将位移变量与旋转变量进一步转化，可以表示为

(21)

式中，ui(x)，wi(x)，θi(x)为位移与转角分量，分别定义为

ui(x)=ξieikix,vi(x)=ηieikix,θi(x)=eikix

(22)

根据非局部轴向力，剪力以及弯矩的表达式，几何位移变量与旋转变梁的波动解形式，可以得到

(23)

式中，Ni(x)，Qi(x)，Mi(x)分别为轴向力、剪力以及弯矩分量，具体表示为

(24)

(25)

(26)

根据前文所介绍的位移、旋转位移分量，对矩阵位移D进行定义，表示为

(27)

进一步，对力矩阵F进行定义，表示为

(28)

根据前文所介绍的边界条件，结合力矩阵以及位移矩阵的表达式，可以得到非局部功能梯度梁的总体矩阵方程为

[K]{Φ}={F}

(29)

式中：Φ为总体转角向量；F为外界力向量，与非局部功能梯度梁所受到的外力相关；K为总体矩阵，具体可以表示为

(30)

式中，B1和B2为边界条件矩阵，由非局部功能梯度梁两端的具体边界情况所决定。对于不同的边界条件，可表述如下：

自由边界条件

(31)

固支边界条件

(32)

简支边界条件

(33)

为了求解非局部功能梯度梁的自由振动特性，外力源向量F可以忽略。采用二分法对总体矩阵进行在一定频率范围内进行零点搜索，得到非局部功能梯度梁的固有频率。将所计算得到的固有频率代入到总体矩阵之中，可以得到非局部功能梯度梁振型等相关信息。

为了求解非局部功能梯度梁的波传播特性，根据控制微分方程，得到关于位移以及转角幅值变量U0，W0，Φ0的代数方程，具体表示为

(34)

式中，T(k,ω)为非对称矩阵，具体表达式由式(13)决定，若齐次方程组存在非零解，其系数行列式必为零，因此可以得到非局部功能梯度梁的频散方程为

detT(k,ω)3×3=0

(35)

通过求解不同波数k对应的波传播频率ω，可以得到波传播频率随着轴向波数的频散曲线，分析其波传播规律。同时，根据波传播频率以及轴线波数，对波传播速度c进行定义，具体表示为

(36)

4 数值结果与讨论

4.1 结果对比验证

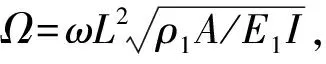
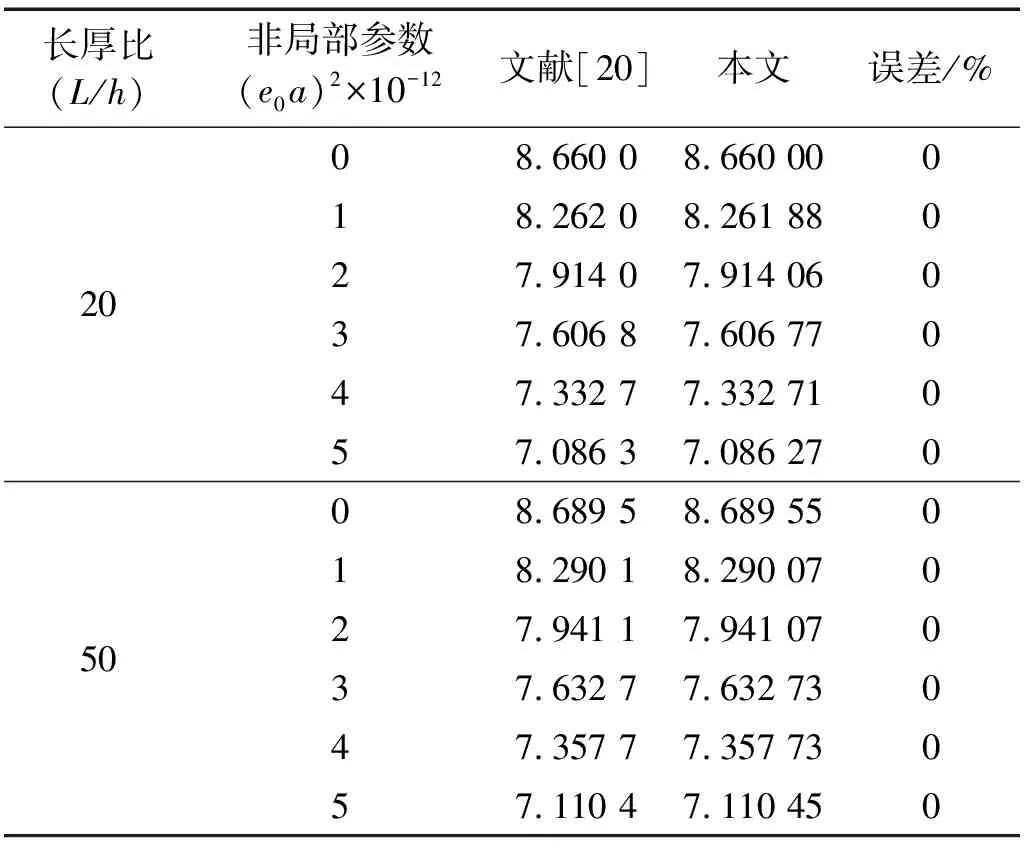
表2 文献数据对比(p=0.2)Tab.2 The comparison of the results with literature (p=0.2)

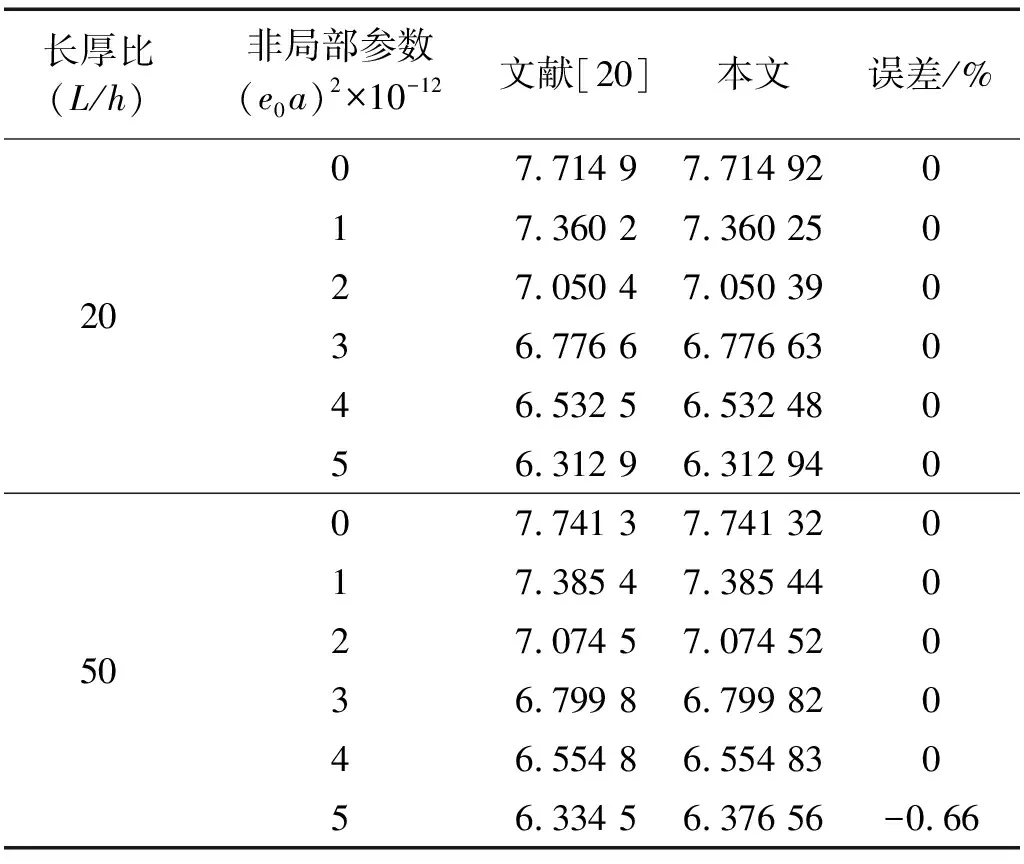
表3 文献数据对比(p=0.5)Tab.3 The comparison of the results with literature (p=0.5)

4.2 非局部参数对固有频率的影响

为了比较分析非局部参数对非局部功能梯度纳米梁自由振动的影响规律，对不同非局部参数下的固有频率进行计算，对频率参数进行比较，总结出非局部参数对固有频率的影响。设置非局部参数(e0a)2变化范围为0～5×10-12，设置功能梯度指数p的变化范围为0.2～5.0，设置长厚比变化L/h为20～100。材料组成以及物理参数设置与表2中的算例相同，边界条件设置为两端简支。非局部参数的影响规律，如图2所示。

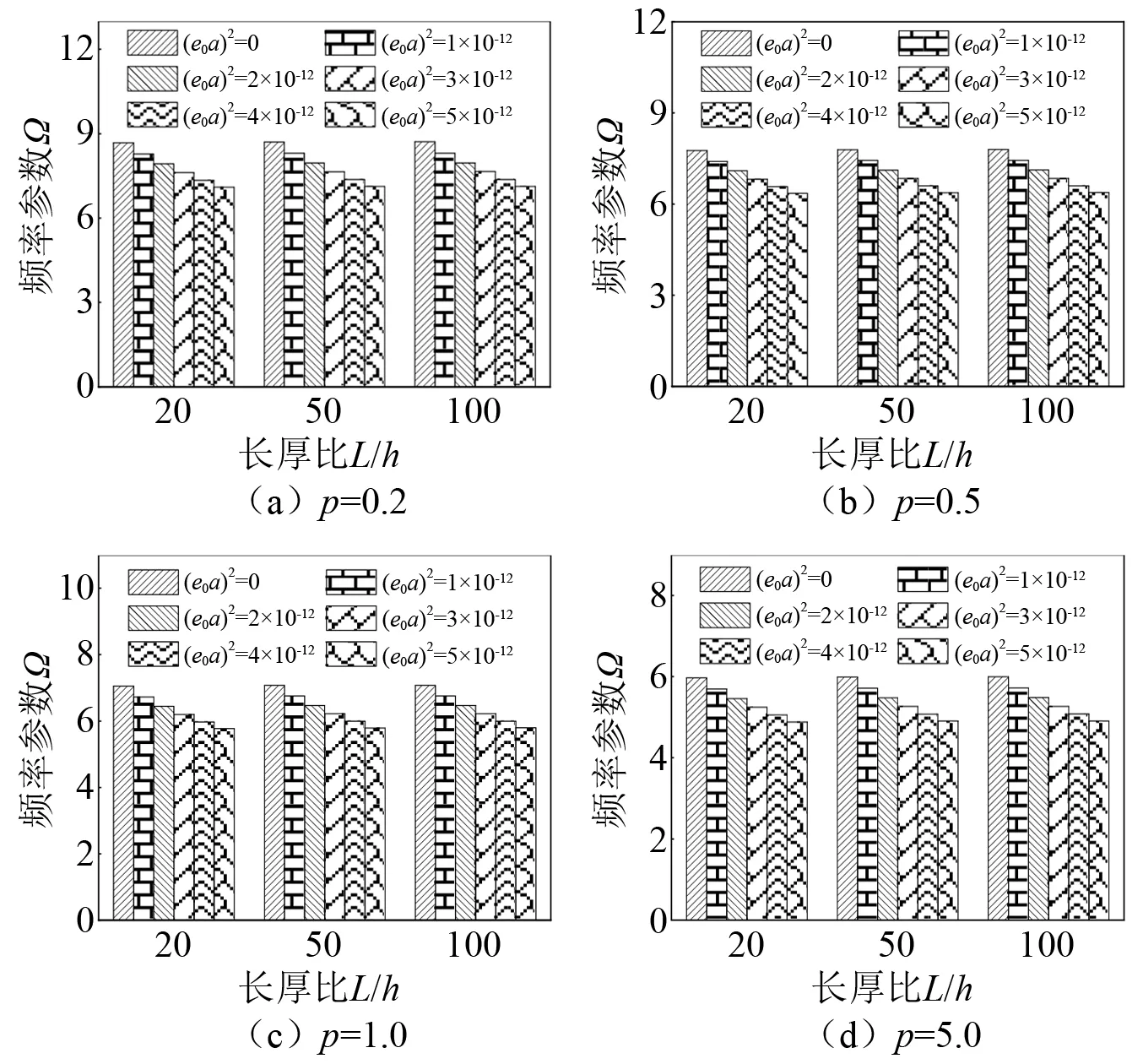
图2 非局部参数的影响规律Fig.2 The effect of nonlocal parameter

通过图2可知，对比不同的功能梯度指数以及长厚比，随着非局部参数的变化，非局部功能梯度纳米梁的频率参数呈现衰减的趋势。因此可以说明，在功能梯度指数一定时，非局部参数的变化对固有频率具有较为明显的影响，随着非局部参数的增大，系统的整体刚度逐渐减小。

4.3 功能梯度指数对固有频率的影响

为研究功能梯度指数p对非局部功能梯度纳米梁自由振动的影响，对不同功能梯度指数对应的固有频率进行计算，通过比较分析，总结归纳功能梯度指数的影响规律。功能梯度指数p分别设置为0.2，0.5，1.0，5.0和10.0，如图3所示。

图3 功能梯度指数的影响规律Fig.3 The effect of power law exponent

从图3可知，对于不同非局部参数以及长厚比对应的频率参数而言，随着功能梯度指数的逐渐增大，频率参数呈现衰减的趋势。因此，当非局部参数一定时，功能梯度指数对非局部功能梯度纳米梁的固有频率存在较明显的影响。

为进一步分析比较分析功能梯度指数对固有频率的影响，选取功能梯度指数p为0.2和10.0状态下的前三阶阵型图进行，如图4所示。同时，展示固支—自由以及自由—简支边界条件下的前三阶振型图，如图5所示。通过比较可知，不同边界条件对非局部梯度纳米梁的振型影响较为明显。

图4 简支边界条件下的模态图Fig.4 The mode shapes of the beam with simply supported boundary condition

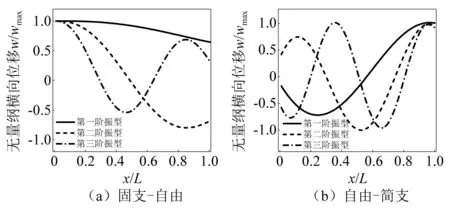
图5 不同边界条件下的振型图Fig.5 The mode shapes for various boundary conditions

4.4 非局部参数对波数以及波速的影响

根据前文所提到的非局部功能梯度梁的动力学控制微分方程，研究分析非局部参数对其波传播频率以及波速的影响效果，其中非局部参数(e0a)2设置为0，1×10-12和2×10-12。不同功能梯度指数条件下，非局部功能梯度梁前三阶波传播频率的变化曲线，如图6所示。从图6可知，当非局部参数取值不同时，功能梯度梁的波传播频率变化规律也不同。当非局部参数为零时，即在经典铁摩辛科梁理论性，波传播频率随着轴向波数的增大而逐渐增大。对于非局部弹性理论而言，在不同功能梯度指数下，当非局部参数分别取不同数值时，波传播频率的变化总体一致；对于第一阶和第二阶传播频率而言，波传播频率逐渐增大并趋于稳定；对于第三阶频率而言，频率逐渐减小并趋于稳定。通过比较可以看出，在非局部弹性理论下，随着非局部参数的增大，波传播频率逐渐减小，并伴有相似的变化趋势。

不同非局部参数下的波传播速度随着波数的变化情况，如图7所示。通过比较可知，当非局部参数为零时，前一阶波传播频率对应的波速逐渐增大，第二阶基本保持稳定，第三阶逐渐减小。同时，前三阶波传播频率对应的波传播速度随着轴向波数的增大逐渐趋于稳定。当非局部参数取不同数值时，波传播速度随着波数的变化曲线基本类似，第一阶波传播频率对应的波传播速度逐渐增大后趋于稳定，第二阶、第三阶波传播频率对应的波速逐渐减小并趋于稳定。同时，随着非局部参数的增大，波传播速度逐渐变小。

图6 非局部参数对于波传播频率的影响Fig.6 The effect of nonlocal parameter on the wave frequency

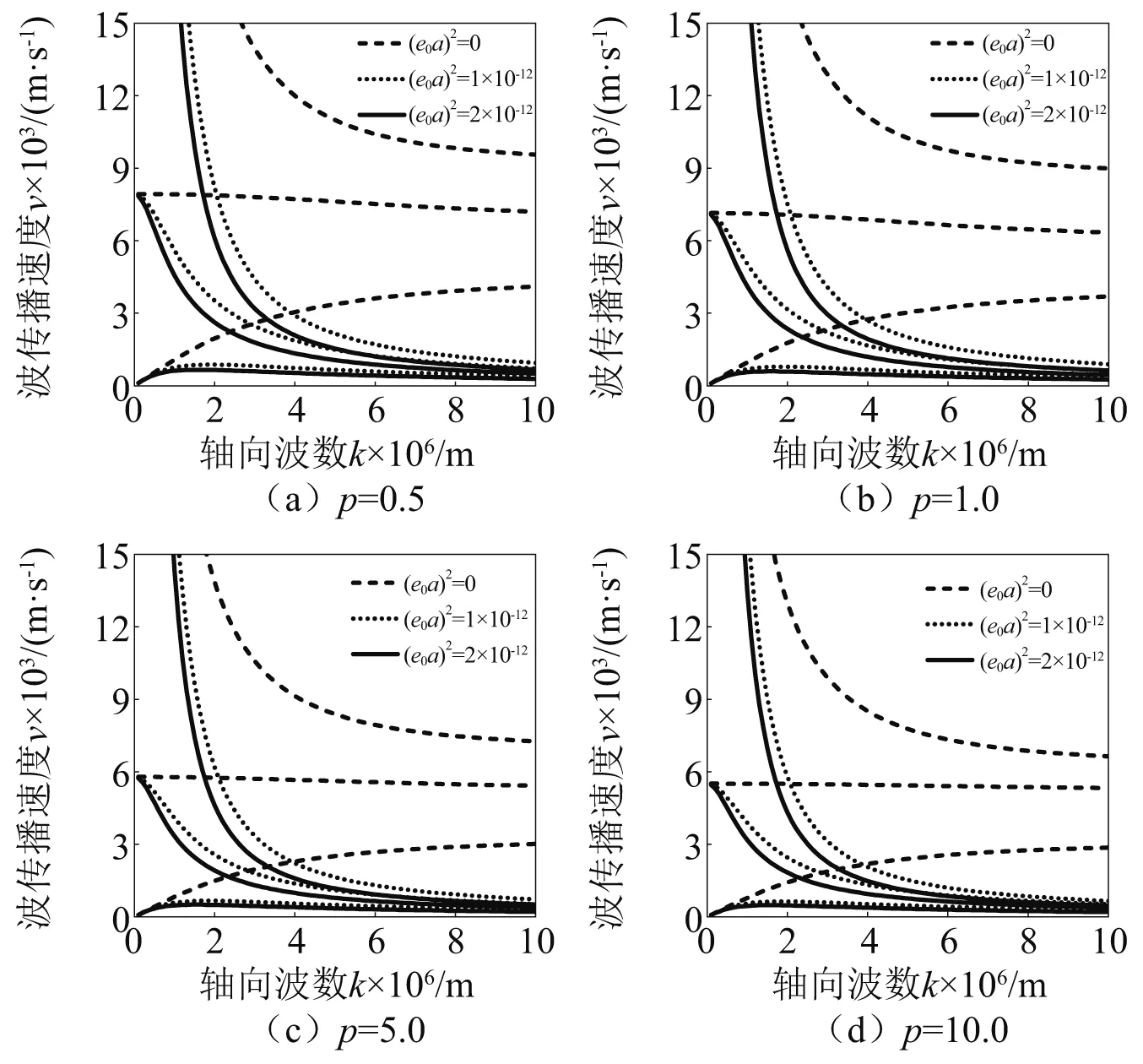
图7 非局部参数对于波传播速度的影响Fig.7 The effect of nonlocal parameter on the phase velocity

4.5 功能梯度指数对波数以及波速的影响

本节主要开展功能梯度指数对非局部梯度梁波传播频率以及波传播速度的影响进行分析研究。通过设置不同的功能梯度指数，比较分析不同情况下波传播频率以及波传播速度随着波数的变化情况，本节所设置的功能梯度指数p分别为0.5，1.0，5.0，10.0。不同功能梯度指数下，波传播速度随着轴向波数的变化情况，如图8所示。从图8可知，当非局部参数为零时，即经典铁摩辛科梁理论下，前三阶波传播频率随着轴向波数的变化逐渐增大。同时，随着功能梯度指数的增大，波传播频率逐渐减小。当非局部参数(e0a)2分别取值1×10-12，2×10-12，3×10-12时，前三阶波传播频率随着轴向波数的变化规律相似。通过比较可以看出，在相同条件下，随着功能梯度指数的增加，波传播频率逐渐减小。

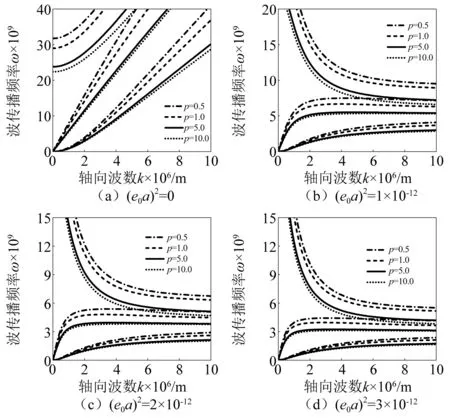
图8 非局部参数对于波传播频率的影响Fig.8 The effect of power law exponent on the wave frequency

不同功能梯度指数下对应的波传播速度曲线，如图9所示。通过比较可知，对于经典铁摩辛科梁理论以及非局部弹性理论而言，前三阶波传播频率对应的波传播速度随着轴向波数的变化规律类似。同时可以发现，在相同的条件下，随着功能梯度指数的逐渐增大，波传播速度逐渐减小。

图9 非局部参数对于波传播频率的影响Fig.9 The effect of power law exponent on the phase velocity

5 结 论

基于非局部弹性理论，建立了非局部功能梯度铁摩辛科梁的控制微分方程。同时，开展了非局部功能梯度梁固有频率以及波传播特性研究。通过与现有文献简支梁的频率结果对比，验证了本文计算方法的正确性。同时，通过比较分析不同非局部参数以及功能梯度指数对非局部功能梯度梁的固有频率变化情况进行对比，得出相应的结论。最后，开展不同参数对非局部功能梯度梁的波传播频率以及波传播速度的影响规律，比较分析不同情况下波传播频率以及波传播速度随着轴向波数的变化曲线，得出相应的结论。

(1) 通过选取算例，与现有文献结果的固有频率参数进行对比，分析与本文结果的误差，验证本文计算方法的正确性，为后续参数化研究奠定基础。

(2) 比较分析非局部参数以及功能梯度参数对非局部功能梯度梁自由振动特性的影响，可以看出，随着非局部参数以及功能梯度参数的增大，对应的频率参数逐渐减小。

(3) 开展非局部功能梯度梁波传播特性的研究，对非局部参数以及功能梯度参数对波传播频率以及波传播速度的影响，分析变化规律，为后续的研究提供一定的理论基础。

附录A

(A.1)

(A.2)

(A.3)

(A.4)

(A.5)