基于Rayleigh法的风机塔筒预应力基本频率解析计算方法
雷振博, 刘 纲,2, 杨 微, 李 杨
(1.重庆大学 土木工程学院,重庆 400045; 2. 重庆大学 山地城镇建设与新技术教育部重点实验室,重庆 400045;3. 中国船舶重工集团海装风电股份有限公司,重庆 401122; 4. 重庆大学 机械工程学院,重庆 400044)
风电作为应对生态环境污染和气候变化的主力军,逐渐得到世界各国的普遍共识和大力发展。统计表明,截至2019年我国风电装机容量已达2.21亿kW,雄踞世界第一[1]。到2050年,我国风电装机容量更有望达到30亿kW,届时将满足国内30%以上的电力需求[2]。风力发电技术将成为我国经济向绿色发展转型、实现碳中和的重要手段。
设计过程中为避免出现共振且同时考虑经济安全等因素,塔筒第一阶频率(基频)往往会远离风轮旋转频率(1f)、过桨频率(3f)以及主要的环境荷载频率[3],故对风力机自振频率的计算精度要求较高。而主流大型风力机塔筒通常采用变截面锥形筒体形式[4],截面刚度随高度呈非线性变化,这给塔筒基频的准确计算带来较大困难。
目前风力机塔筒自振频率计算主要有解析和数值计算两类方法。在解析计算方面,Byrne[5]将塔筒结构等效为悬臂梁,将机舱和风轮等效为顶部集中质量,基于结构动力学原理,获得塔筒等效单自由度体系基频计算公式。牛文杰[6]考虑桩-弹性地基作用影响,采用柔度法对风机结构进行多自由度动力分析,通过求解微分方程确定风力机塔筒基频。在数值计算方面,杨春宝等[7]考虑风力机塔筒变截面特性,建立了近海风力机塔筒自振频率求解数值计算方法,并利用实际工程进行有效性验证。曾梦伟等[8]将风轮与机舱等效为质量点,建立机舱-塔筒-法兰刚柔多体耦合精细化有限元模型,采用数值模拟方法计算塔筒结构自振频率。田英鹏等[9]将风力机法兰和螺栓连接视为刚性连接,将风轮、机舱及法兰等效为质量点,采用壳单元构建塔筒结构有限元模型进行基频计算,并通过试验验证了计算精度。
总体而言,采用精细化有限元模型能够较为准确获得风力机塔筒的基频,但建模工作量极大,并不适合于塔筒前期设计的简化、快速计算。而目前解析方法较为简略,未考虑塔筒截面变刚度特性、机舱和风轮载荷引起的塔筒预变形,计算精度不高,难以满足工程实际需求。针对以上问题,根据风机塔筒结构构造形式及力学特征,计入机舱及风轮质量对塔筒的预应力作用,提出基于Rayleigh法的风机塔筒预应力基频解析计算方法。同时,考虑塔筒变形形状、顶部集中质量偏心等多种情况,构建塔筒基频工程实用解析计算方法,为风力机塔筒设计及共振控制提供方法支撑。
1 能量法基频计算原理
1.1 风力机塔筒模型简化
锥台型塔筒由数段钢制锥筒通过法兰盘连接而成,每段锥筒的直径、壁厚均不一致,由底向上逐渐减小,如图1(a)所示。大量研究、试验和现场实测表明,塔筒主要沿顺风向和横风向振动,且往往以顺风向为主,故可将空间塔筒简化为二维模型,取塔筒底面中心点为坐标原点,沿竖直方向为z轴,沿顺风向为x轴,如图1(b)所示。
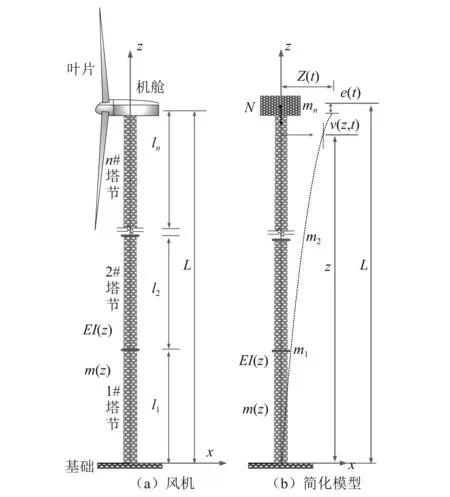
图1 风机等效单自由度结构Fig.1 Equivalent single degree of freedom flexible structure
由图1可知,塔筒由n段钢制塔段及n-1个法兰盘组成,塔段从下至上的高度分别为l1,l2,…,ln,塔筒总高为L。考虑塔筒沿高度方向具有变化的弯曲刚度EI(z)及质量密度m(z)。法兰盘质量依下至上为m1,m2,…,mn-1,塔筒顶部机组及风轮的质量记为mn,其对塔筒的预应力为集中质量自质量产生的轴向压力N=mng。
1.2 能量法自振频率计算原理
为方便采用能量法建立风力机塔筒运动方程,可将塔筒近似等效为单自由度体系[10]。根据结构动力学原理,假设塔筒某阶振动的形状函数为ψ(z),则高度z处塔筒在t时刻的位移v(z,t)为
v(z,t)=ψ(z)Z(t)
(1)
式中:Z(t)为广义坐标,表示t时刻塔顶处x向的位移大小。
根据虚功原理可得塔筒广义单自由度体系的运动方程为
(2)
其中,
(3)
式中:m*为广义质量;c*为广义阻尼;k*为广义弯曲刚度。
结合Rayleigh能量法和式(3),可推导得到塔筒广义单自由度体系的基频为[11]
(4)
2 考虑预应力的基频解析方法
2.1 塔筒预变形
大量文献表明,塔筒在顶部机舱、风轮载荷作用下会产生压应力和预变形,塔筒中的压应力会导致塔筒刚度变化,进而影响塔筒频率[12]。因此,机舱、风轮载荷引起压预应力效应是影响风机塔筒基频的重要因素之一。
假定塔筒在机舱、风轮载荷下产生的预变形为e(t)(见图1(b)),根据几何关系有
(5)
故考虑预应力的塔筒基频为
(6)
塔筒的广义单自由度体系的运动方程为
(7)

(8)
式中,δe(t)为对预变形为e(t)的变分。
对比式(4)和式(6)可知,塔筒机舱、风轮载荷作用下产生的压应力将降低塔筒基频。
2.2 平均等效当量惯性矩及壁厚
塔筒沿高度方向具有变化的壁厚及截面直径,故简化基频计算时,采用等效壁厚t*来表示塔筒壁厚的影响[13],其表达式为
(9)
式中:li为第i段塔筒高度;ti为第i段塔筒壁厚。
针对截面变直径引起塔筒沿高度刚度变化问题,基于位移等效原理,采用平均等效当量惯性矩I*近似计算[14]
(10)
式中:i1为系数,当考虑塔筒顶部横向集中荷载作用时i1=3,当考虑塔筒横向均布荷载作用时i1=4;Ii为通过积分获得的第i段塔筒的惯性矩,其表达式为
(11)
式中:Di为第i段塔筒的底部中直径;di为第i段塔筒的顶部中直径。
3 多参数影响下基本频率分析
3.1 考虑塔筒变形形状影响
由Rayleigh法基本原理可知,基频计算精度依赖于所取形状函数与真实振型的相似度,对典型悬臂结构,通常以集中荷载或均布荷载变形下的挠曲线作为形状函数。风力机塔筒结构的力学模型,如图2所示。

图2 风机变形影响因素Fig.2 Influence factors of fan deformation
3.1.1 塔顶集中荷载
如图2(a)所示。根据材料力学可知,悬臂柱自由端作用水平集中荷载产生的挠曲线为[15]
(12)
将式(12)代入式(1)可得塔顶集中荷载下塔筒变形的形状函数为
(13)
将式(13)代入式(6)可得集中荷载作用下,考虑预压应力影响的塔筒基频表达式为
(14)
式中:ρ为材料密度;D为整个风力机塔筒底部中直径;d为顶部中直径。
3.1.2 均布荷载
由材料力学可知,悬臂柱横向作用水平均布荷载产生的挠曲线为
(15)
将式(15)代入式(1)可得均布荷载下塔筒变形的形状函数为
(16)
将式(16)代入式(6)可得均布荷载作用下,考虑预压应力影响的塔筒基频表达式为
(17)
3.2 考虑顶部质量偏心影响
由于塔筒顶部的机舱、叶轮在x向有偏心,即图2(b)中集中力N与塔筒的中心轴有偏心距Δ。塔顶质量偏心将引起附加弯矩,则塔筒广义几何刚度应修正为
(18)
将式(13)、式(18)代入式(6),式(16)、式(18)代入式(6)可分别得到集中荷载作用下考虑偏心的塔筒基频f3、均布荷载作用下考虑偏心的塔筒基频f4为
(19)
4 数值算例
4.1 3.4 MW-100塔型
以两个风机塔筒为例,通过有限元数值计算结果验证所提塔筒基频计算公式的适用性。塔筒1为某3.4 MW风机100 m高塔筒,该型风机的机舱质量为126.75 t,风轮质量为96.5 t;风机塔筒整体呈圆台状,塔筒计算总高度为96.7 m;塔筒分节及截面详细尺寸,如表1所示。塔筒材料采用Q345钢,弹性模量取为2.06×105MPa,密度取为7 850 kg/m3。塔筒顶部风轮沿x方向偏心-4.475 m,机舱沿x方向偏心0.953 m,沿y向偏心-0.038 m。

表1 塔筒几何参数Tab.1 Tower geometry parameters
通过ANSYS软件建立该塔筒的有限元壳模型,并计入塔顶机舱、风轮质量偏心的影响。塔筒选用SHELL63单元模拟,并考虑实际塔筒的渐变分段效果。顶部机舱和风轮以及各法兰盘等效为点质量,采用MASS21单元模拟。塔筒底部与基础固定连接,建立的有限元模型如图3所示。
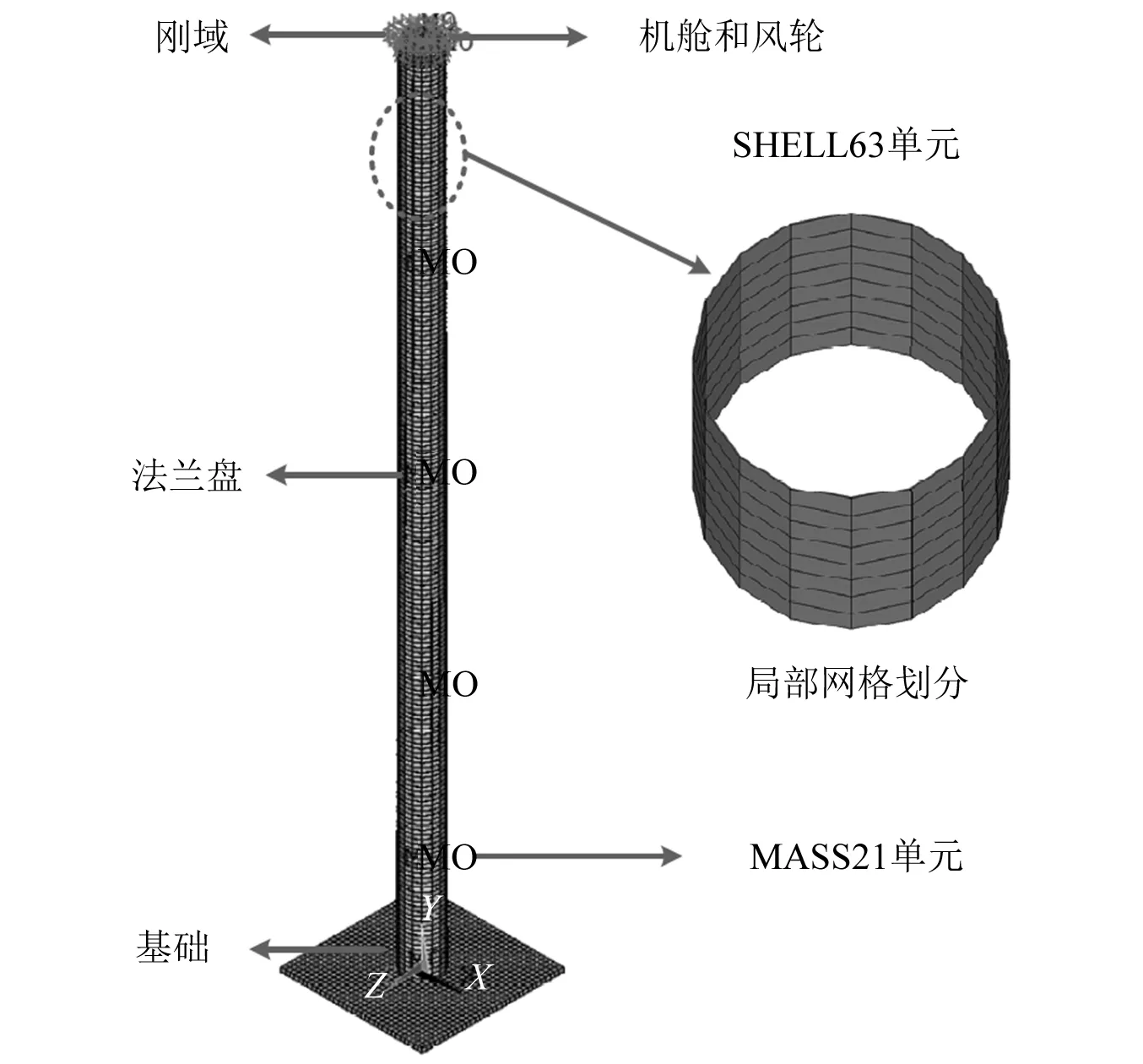
图3 风机塔筒有限元模型示意图Fig.3 Finite element model of wind turbine tower
预应力模态分析通过有预应力的模态分析方法来实现,有预应力结构的固有频率和模态计算,需要先进行结构的静力分析获得应力刚度矩阵,将其代入频率分析方程来得到考虑机舱和风轮质量预应力的模态分析[16]。通过模态分析,获取塔筒x向和y向的基频如图4所示。
从图4可知,塔筒在x向和y向第一阶频率分别为0.222 Hz和0.225 Hz。根据式(14)、式(18)和式(19),计算得到不同条件下的风机塔筒基频,如表2所示。

图4 100 m风机塔筒预应力模态示意图Fig.4 Pre-stress mode diagram of 100 m wind turbine tower
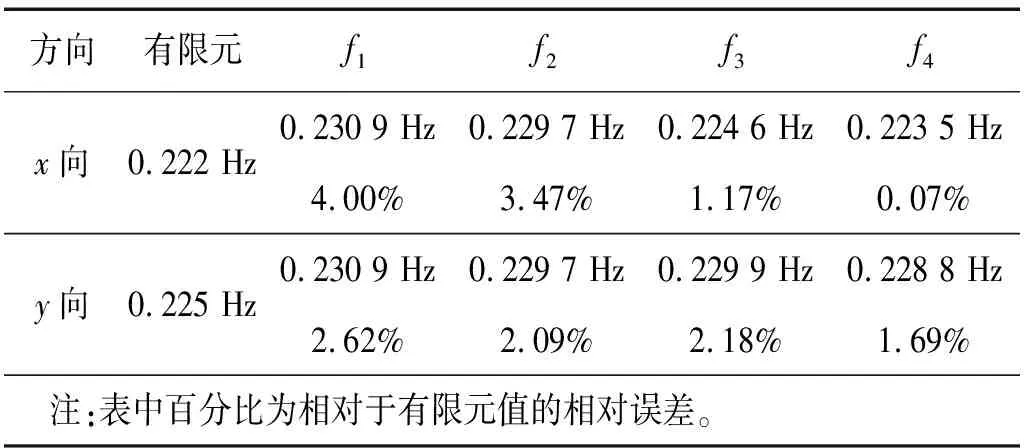
表2 100 m塔筒基频计算结果对比Tab.2 Frequency calculation of 100 m wind turbine
4.2 3.4 MW-90塔型
塔筒2为某3.4 MW风机90 m高塔筒。该型风机的机舱质量为126.75 t,风轮质量为101.72 t;风机塔筒整体呈圆台状,塔筒计算总高度为86.7 m;塔筒顶部风轮沿x方向偏心-4.475 m,机舱沿x方向偏心0.953 m,沿y向偏心-0.038 m。同4.1节相同建模方法,采用ANSYS有限元软件计算得到塔筒在x向和y向基频分别为0.262和0.265。根据式(14)、式(18)和式(19),计算得到不同条件下的风机塔筒基频如表3所示。
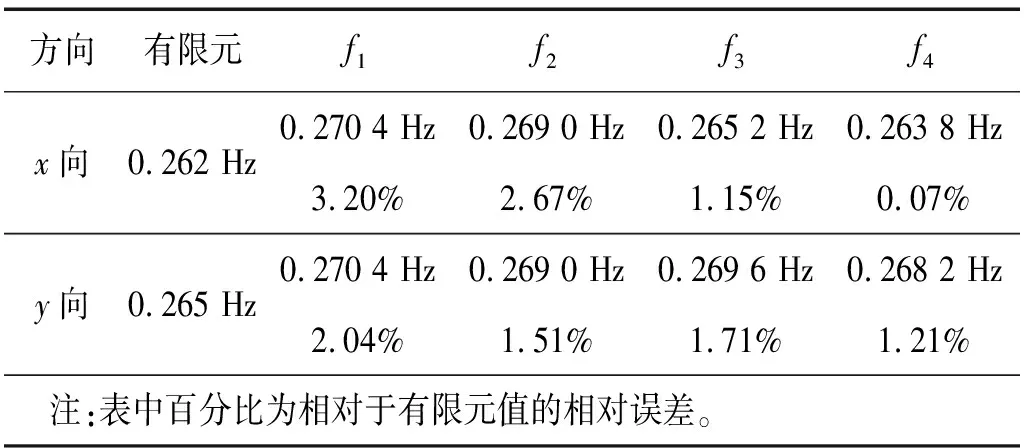
表3 90 m塔筒频率计算结果对比Tab.3 Frequency calculation of 90 m wind turbine
从表2、表3计算结果可知,无论x向还是y向,采用Rayleigh能量法所得基频均高于精细化有限元模型计算值,这主要因为能量法计算所假设的变形公式式(13)、式(16)均无法与真实变形曲线完全吻合所致;相比而言,f2,f4较f1,f3更加接近于有限元数值解,因此,宜采用均布荷载作用下的形状函数进行解析法计算。同时,因x向偏心较大,考虑顶部质量偏心对x向基频计算精度有显著影响,在集中荷载变形下,塔筒1和塔筒2的精度分别可提高2.8%和1.9%,均布荷载变形下分别可提高3.4%和2.6%。故当顶部质量偏心较大时,应考虑偏心对解析法求解的影响。
5 试验验证
5.1 模型设计
以塔筒1为原型在实验室搭建试验塔筒,模型几何相似比Sl为1/20。由于原型筒壁最薄处仅14 mm,无法完全遵守几何相似关系进行缩尺,故主要保证模型与原型动力特性相似,即保证构件截面弯曲刚度相似与质量分布相似[17-18]。通过材性试验测得其弹性模量为1.525×105MPa,为保证加工精度可控,模型塔筒每节截面和壁厚不变,按原型塔筒相应节底截面进行相似设计,试验塔筒模型几何参数如表4所示。
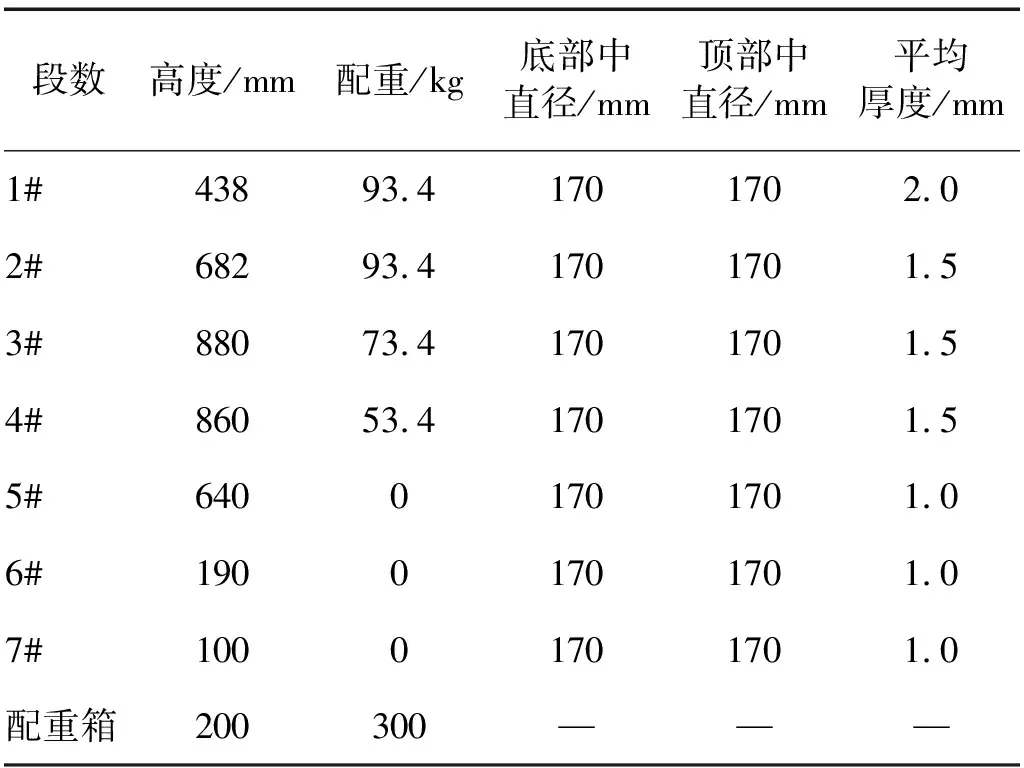
表4 模型几何参数Tab.4 Model geometric parameters
与原型塔筒对应,模型塔筒总共分5段,段与段之间由法兰连接,法兰盘上设置配重篮,塔筒顶部设置配重箱考虑机舱和风轮质量。模型由Q345热轧钢板焊接而成组成,底部法兰连接600 mm×600 mm×20 mm的矩形连接板,并通过18颗螺栓和钢板连接。试验模型顶部配重箱沿x方向偏心6 cm。筒体与法兰之间采用对接焊缝连接,各法兰间采用螺栓连接,如图5所示。
5.2 测点及加载方案设计
在各配重篮和顶部配重箱的x和y向均布设P15H-2压电加速度传感器(见图5)。

图5 试验模型Fig.5 Experiment model
5.3 频率测试
在塔顶施加锤击激励使其产生自由振动,测得塔顶加速度时程如图6所示。通过傅里叶变换,得到塔筒两个方向的功率谱如图7所示。
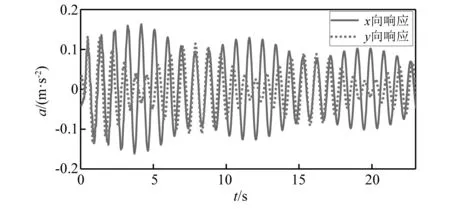
图6 塔顶加速度响应时程曲线Fig.6 Acceleration response at the top of tower
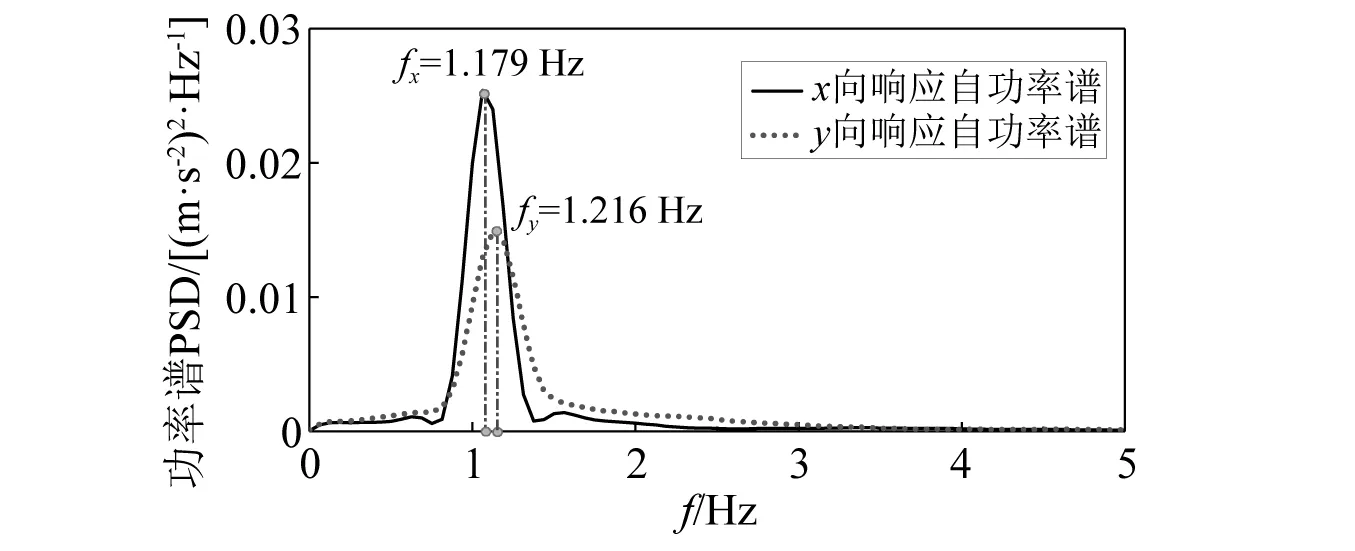
图7 加速度功率谱Fig.7 Acceleration power spectrum
从图7可看出,模型对应x向和y向基频分别为1.18 Hz和1.22 Hz。同时,试验中仅采用顶部激励时,图6的加速度响应出现典型的拍频振动特征及正交耦合现象,表明试验模型的振动符合高柔结构的响应特征[19-21]。加速度功率谱仅有一个峰值,表明塔筒以第一阶振动为主,这与大多数文献及试验结果相吻合[22-24]。
5.4 有限元数值模型
与4.1节相同建模方法相同,弹性模量采用材性试验测得的1.525×105MPa。结合表4模型几何参数,采用ANSYS有限元软件计算试验缩尺模型的x向和y向基频分别为1.203 Hz和1.212 Hz。x向和y向的基本频率与试验测试的基频误差均在3%以内,与试验测试值吻合较好。
5.5 解析法对比验证
结合传统风力机塔筒频率解析方法及式(18),计算可得试验模型解析法的理论值与动力测试基频,如表5所示。
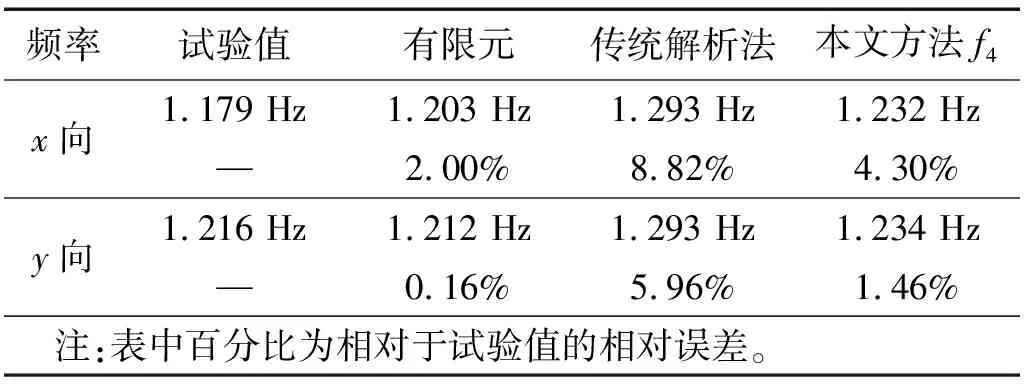
表5 理论值与实测值对比Tab.5 Comparison between calculation and experiment
从表5可知,试验塔筒在x向实测基频低于y向基频,这主要是因为该塔筒在x向存在偏心,将减少塔筒在该向刚度,故实测频率值偏小,故在计算塔筒基频时有必要计入偏心影响。就传统解析法和本文所提方法而言,后者较前者更加精确,即x向计算精度提高4.52%,y向计算精度提高4.50%。这主要是因为本文方法综合考虑了机舱、风轮质量和偏心,以及塔筒不同变形形状等情况的影响。
6 结 论
针对风力机塔筒基频解析计算精度难以满足工程要求的问题,提出一种基于Rayleigh法的风力机塔筒基频快速估算方法。考虑机舱、风轮质量对塔筒压力作用,以及塔筒不同变形形状函数、顶部集中质量偏心等系列实际情况,基于理论推导给出了解析计算公式,并通过数值算例与缩尺模型试验验证了所提方法的适用性及有效性。所得结论如下:
(1) 有限元模型与试验结果均表明采用均布荷载作用下的变形形状曲线将得到更高的解析计算精度,两个数值算例中,f2和f4与有限元模型计算值的最大相对误差仅为3.47%。因此,宜采用均布荷载作用下的挠曲线作为Rayleigh法的形状函数。
(2) 顶部质量偏心对塔筒基频计算精度有显著影响,特别是在偏心距较大时。采用集中荷载作用下的变形曲线时,考虑偏心情况下塔筒1和塔筒2的精度分别可提高2.8%和1.9%;采用均布荷载作用下变形曲线时,考虑偏心情况下塔筒1和塔筒2的计算精度分别提高3.4%和2.6%。因此,在计算风机塔筒基频时,应考虑机舱、风轮质量偏心的影响。
(3) 缩尺模型试验表明,本文方法考虑了机舱、风轮质量及偏心,以及塔筒不同变形形状等多种情况的综合影响,x向基频计算精度可提高4.52%,y向基频计算精度可提高4.50%,较传统解析方法更加精确。

