基于CFD的地面颤振模拟试验非定常气动力重构方法研究

宋巧治， 王彬文， 李晓东

(中国飞机强度研究所 飞机结构振动技术研究室，西安 710065)

飞行器颤振是由结构与空气相互耦合而发生的一种气动弹性失稳现象，颤振问题对飞行器的飞行安全构成很大威胁。虽然颤振主动抑制算法研究较多，但是距离工程实用尚有一定的距离，因此目前防止颤振发生的有效途径是通过分析和试验获得准确的颤振边界并严格控制飞行速度在颤振包线以内。目前的颤振的验证手段主要有风洞试验和飞行试验[1]，两者都具有周期长、成本高、风险高的特点，因此国外学者提出了一种地面颤振模拟试验验证方法，通过在地面重构结构的非定常气动力实现颤振边界的测试。

地面颤振模拟的概念最早由Kearns[2]提出，1974年法国的Rajagopal研究了二自由度舵面模型的地面颤振模拟试验，但是由于缺乏先进的数字计算机技术，因此只能成为一个设想。随着硬件条件的发展，地面颤振模拟试验得以实现，Karkle等[3]研究了地面颤振模拟试验方案，并进行了舵面颤振和导弹气动伺服弹性特性测试； Zeng等[4]系统地研究了气动力重构和激励力控制方法，基于平板结构对地面颤振模拟试验进行了验证。Liseykin等[5]在非线性颤振验证进行了初步应用尝试。Dhital等[6-7]研究了气动力等效降阶的方法。

国内潘树祥等[8]在20世纪80年代就开始了地面热颤振模拟试验技术研究，通过石英灯加热的方式模拟气动加热环境，对热环境下结构的颤振特性进行了测试，为热颤振验证提供了一种可行手段。Wu等[9-11]研究了气动力重构以及气动力模拟加载控制等问题，并利用导弹模型等结构的对方法进行了验证。胡巍等[12]实现了带有舵面结构的气动力重构方法。邵崇晖[13]研究了地面颤振模拟试验在壁板结构的颤振测试中的应用。

1 非定常气动力重构

影响地面颤振模拟试验的因素主要为重构气动力的精度，当前国内外大多数研究都是基于频域气动力模型，气动力计算的精度在跨音速范围内较差，因而限制了地面颤振模拟试验应用马赫数的范围。基于计算流体动力学(computational fluid dynamics,CFD)的时域方法具有较高的计算精度，但是计算效率较低。由于实际飞行过程中的非定常气动力作用是实时的，因此要求重构的气动力模型具有实时性，为了将CFD方法用于地面颤振模拟试验中，需要研究模型降阶方法，提高气动力的计算效率。

跨音速飞行中由于激波的出现，气动力呈现较强的非线性特性。Dowell[14]经过研究后发现在跨音速范围内，虽然气动力整体是非线性的，但是非线性主要体现在静压背景，而非定常气动力在结构作小幅值振荡时，仍可以认为是线性的，仿真分析也证明了Dowell假设的准确性，该研究为后续降阶模型(reduced order model，ROM)奠定了基础。

近年来，模型降阶方法开始应用于非定常气动力计算中。鉴于气动力降阶能够大幅提升计算效率，因此国内外学者对降阶方法开展了大量研究，并形成了众多的成果，当前方法按照原理主要分为三类：基于系统辨识的方法、基于流场模态的方法以及正交投影分解(proper orthogonal decomposition，POD)方法[15]。

基于系统辨识的方法由于原理简单，是其中较为常用的一种方法，该方法在降阶过程中需要对分析模型进行激励，以便获得较宽频带范围的系统输入和输出信号，然后利用输入和输出建立气动力降阶模型。Gupta等[16-17]提出了以颤振飞行试验中常用的3211信号作为激励形式的非定常气动力降阶方法，后期经过发展逐渐成熟。张伟伟等[18]基于3211信号对气动力降阶模型进行了研究，认为该信号激励频带较宽，但是需要反复调节信号的周期以充分激励期望的频带。

本文在气动力模型降阶的基础上，提出坐标转换方法，建立物理坐标系下的气动力模型，同时对插值点进行缩聚，满足地面颤振模拟试验插值点的数量要求，最终建立了地面颤振模拟试验可用的非定常气动力模型。

2 气动力模型重构原理

常用的气动力降阶模型大都基于广义坐标建立，而地面颤振模拟试验中需要的是物理坐标下的气动力模型，为了完成气动力模型由广义坐标向物理坐标的转换，推导了两个坐标系的相互转换关系。同时基于广义力等效的方式，完成了物理坐标系下的气动力缩聚模型的建立，具体流程如图1所示。

图1 非定常气动力重构方案Fig.1 Scheme of unsteady aerodynamic reproduction

3 气动力模型降阶

以跨音速标准模型AGARD445.6机翼作为验证对象，该机翼采用NACA65A004对称翼型，具有明显的跨音速气动特征，半展长762 mm，1/4弦处后掠角45，展弦比(展长与平均弦长)1.652 5，跟梢比0.66，模型尺寸如图2所示。

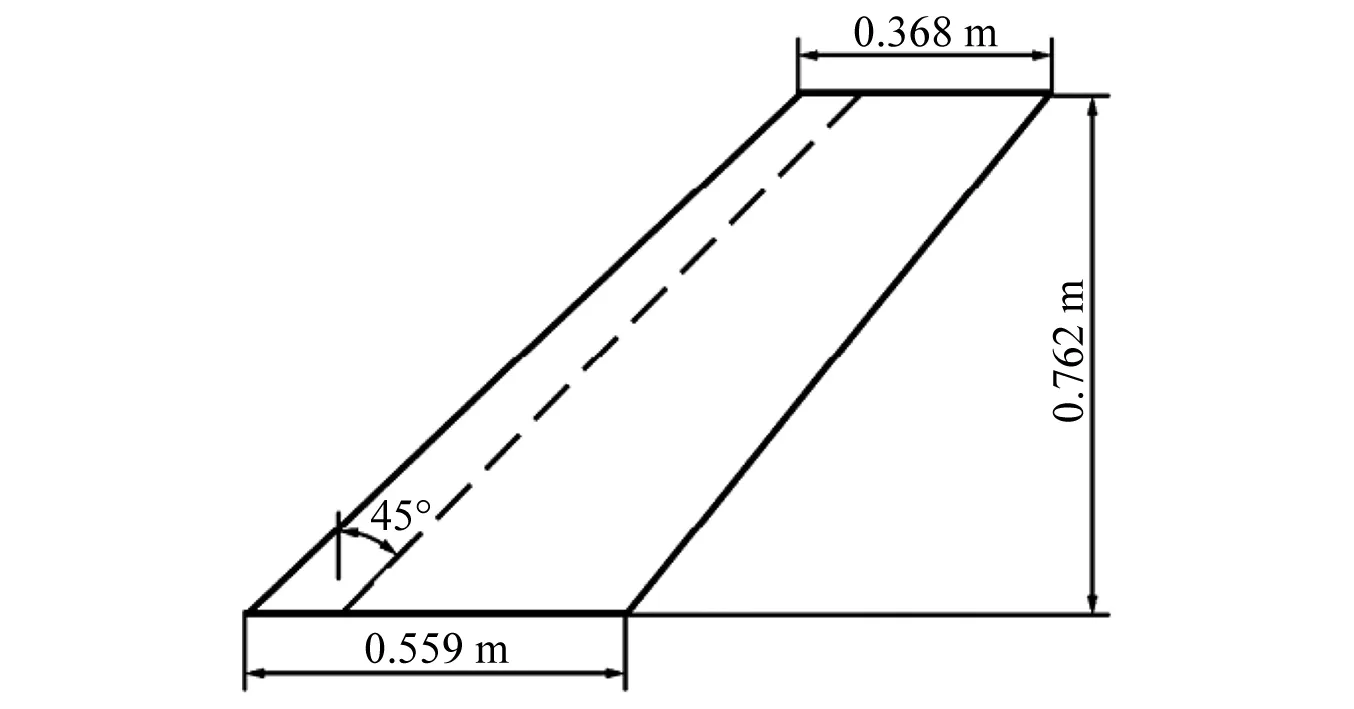
图2 AGARD445.6机翼模型尺寸Fig.2 Model size of AGARD445.6 wing

为了对模型进行分析，首先建立了结构的有限元模型，通过调节材料特性参数，使分析模态频率与试验结果吻合，表1为最终分析结果与试验结果对比，可以看出模型与试验结果前四阶模态频率误差都在1%以内，证明分析模型能够反映真实结构的动态特性。

表1 分析结构模态频率与试验结果对比Tab.1 Comparison of model frequency between analysis and test

为了获得结构的颤振边界，基于CFD/CSD(computational fluid dynamic/computational solid dynamic)耦合的方法进行分析，求解采用无黏Euler方程、理想气体模型，空间离散采用二阶迎风格式，物理时间步长设置为0.002 s，通过给定大气来流条件，分析不同动压条件下的结构响应趋势，得到了结构的颤振边界，计算来流条件如表2所示，结构和气动网格如图3和图4所示。

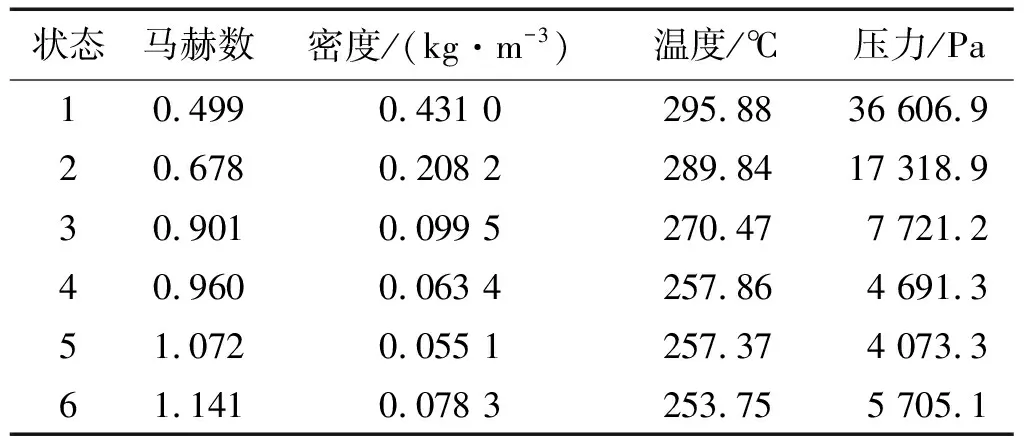
表2 颤振计算大气状态条件Tab.2 Airflow condition of flutter analysis

图3 结构网格划分Fig 3 Mesh generation on structure

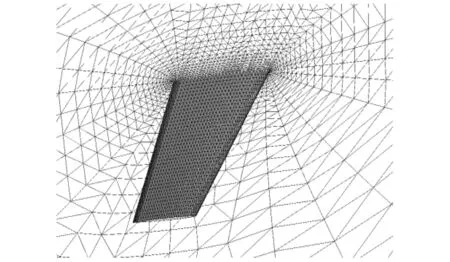
图4 结构表面及对称面气动网格Fig.4 Fluid mesh on wing surface and symmetry

设计了用于模态激励的3211信号，以结构前四阶模态振型作为强迫位移分布，各阶模态的幅值均设置为0.001 5，四阶模态的广义位移幅值见图5。通过流固耦合分析，获得结构节点的非定常气动力向量，并利用坐标变换计算获得结构的广义气动力。

图5 前四阶模态强迫位移幅值Fig.5 Forced displacement magnitude of first four modes

以广义位移为输入，广义气动力为输出，采用自回归滑动平均ARMA模型对气动力进行系统建模，该模型离散时间形式为[19]

(1)

式中：y为CFD计算输出广义气动力向量；u为CFD系统输入广义位移信号；na，nb分别为输出、输入延迟阶数，本例中均取6；k为离散时间变量；A，B为系统模型待辨识参数。通过系统辨识建立了气动力降阶模型，在Ma=0.96的状态下，前四阶模态的广义力与降阶模型输出结果对比情况，如图6所示。由图6可知，降阶模型与原始模型的吻合度较高，同时也可以看出给定的3211激励信号激励下，模型的各阶广义力响应都比较明显，因此可以证明设定的激励信号满足模态激励的要求。

图6 结构前四阶模态广义气动力Fig.6 The generalized force of first four modes

经过以上降阶过程，建立了广义坐标下的气动力影响系数矩阵Qhh，但试验过程中使用的物理量必须是在物理坐标下描述的，为此需要完成广义坐标下物理量与物理坐标下物理量的相互转换。

4 坐标变换

由结构模态分析理论可知，结构响应和激励力的广义坐标和物理坐标定义为

x=Φq

(2)

F=ΦTf

(3)

式中：x为物理坐标下结构位移响应；q为广义坐标，Φ为模态矩阵；F为广义力；f为物理坐标下力向量。

由于模态矩阵本身不具备正交性，模态变换方程不能直接通过前乘振型矩阵完成，同时考虑到结构有限元节点往往数量众多，求解获得所有阶次模态矩阵较为困难，因此无法对模态矩阵求逆以完成上述转换，为了解决上述转换问题，利用了模态矩阵关于质量阵正交(假设模态矩阵按照质量阵进行归一化，见式(4))这一特性完成坐标变换。

ΦTMΦ=I

(4)

式中，M为结构的质量矩阵。

ΦTMx=ΦTMΦq

(5)

整理可得

q=ΦTMx

(6)

式(6)完成了响应由物理坐标向模态广义坐标的转换。

力的坐标变换不能直接通过前乘矩阵的方式完成变换，为此采用如下假设，即如果两种物理坐标下力向量分布转换为广义力等效，则结构的模态响应也等效，同时考虑到对颤振影响的主要模态为低阶模态，因此低阶模态广义力等效即可保证颤振边界的等效，假设节点力向量服从以下分布

f=MΦf0

(7)

式中，f0为假设的任意向量，则相应的广义力为

F=ΦTf=ΦTMΦf0=f0

(8)

代入式(7)可以得到

f=MΦf0=MΦF

(9)

由于MΦ为满秩矩阵，MΦf0可以生成所有向量，上述假设不失一般性。因此由式(9)可以实现模态广义坐标下的力到物理坐标下的节点力向量转换，物理坐标下的气动力影响系数矩阵可以描述为

Qkk=MΦQhhΦTM

(10)

通过式(10)操作建立了物理坐标下降阶气动力模型，该模型以结构节点响应为输入，以结构节点气动载荷为输出。由于模型的输入是所有节点的响应，输出是全部节点的气动载荷，而在地面颤振模拟试验中，受设备数量和空间位置的限制，能够记录的结构节点响应和模拟的气动载荷加载点数量有限。为了能够满足试验要求，需要对结构插值节点进行缩聚处理。

罗扎诺夫的写作方法简直快赶上当下的某些“身体写作”了。 我们似乎不应该误解其写作的“身体性”，而是应该把“身体性”理解为极度的“任性”。 他说：

5 插值节点缩聚

颤振控制方程可以通过式(11)描述

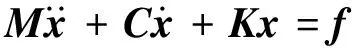
(11)

式中：M，C，K分别为结构的质量阵、阻尼阵和刚度阵；x为节点响应列向量；f为气动力向量，可以通过式(12)计算获得

f=qdMΦQhhΦTMx

(12)

式中：qd为来流动压；x为所有节点的响应；f为所有节点的气动力。为了使结构的颤振特性不发生改变，节点缩聚需要满足条件：①根据缩聚后节点能够获得与全部节点等效的变形；②缩聚后节点力能够等效所有节点的节点力。

为了满足上述两个条件，引入了插值方法，由于本文采用的结构模型为三维模型，因此插值采用薄板插值(thin panel spline, TPS)方法，薄板插值方法变形控制方程为

(13)

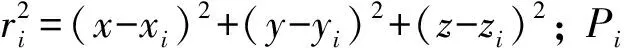
无限远处边界条件定义为

(14)

利用插值点构造满足边界条件的变形场，由此可以得到插值矩阵

h=GTPSx

(15)

式中，GTPS为插值矩阵，若要第一个条件满足，则应有

‖x-Grxr‖<ε

(16)

式中：x为所有节点响应向量；xr为缩聚后节点响应向量；Gr为r集到s集节点的插值矩阵；ε为任意小量。引入模态变换，则有

Δ=‖Φs-GrΦr‖<ε

(17)

式中：Φs为模型所有节点模态振型矩阵；GrΦr为缩聚后节点振型矩阵在所有节点上的插值。

仅考虑低阶模态，如果缩聚后节点振型矩阵在所有节点上插值与所有节点模态振型矩阵等效，则条件1满足；

在条件1满足情况下，根据虚功原理，则有式(18)成立，条件2满足

(18)

为了使条件1满足，采用了优化算法对缩聚节点的位置进行了优化，采用4激振点和4个拾振点的配置方案，优化方法采用遗传算法，采用缩聚后节点前两阶模态振型在所有节点上的插值振型与原始振型的差异最小作为优化的目标函数，由于结构的振动响应主要沿Z方向，因此本文中计算振型只考虑Z方向的分量，其他方向不做考虑，优化变量取缩聚后节点位置，由于实际试验中边界处的约束条件自动满足，因此在缩聚过程中，增加了边界处的虚拟插值点以对应实际的边界条件。

由于结构颤振发生时，颤振的主参与模态集中在低阶模态，因此采用模态叠加原理，若要使式(17)成立，则应该有式(19)成立

Δ1=‖Φs1-GrΦr1‖<ε

(19)

式中：Φs1为关心的结构模态的振型；GrΦr1为选择的测点处的振型分量在整个结构节点上的插值，通过优化算法进行求解，使两者的偏差Δ1最小，即可利用少量测点代替所有结构节点的目标。

优化选取的插值点位置，如图7所示。为了对插值点缩聚效果进行说明，计算了缩聚后的插值振型并与原始振型进行了对比，如图8所示。采用缩聚后插值振型与原始振型的MAC值作为插值的等效的衡量指标，基于优化插值点位置获得的前两阶模态振型与原始振型的MAC值分别为0.98和0.94，证明缩聚模型具有较高的精度。

图7 优化获得的激振点(拾振点)位置Fig.7 Shaker location after optimization

经过缩聚可以实现利用少量激振点和拾振点即可满足气动力等效模拟的要求，最终的气动力计算模型如式(20)所示，xr为缩聚后节点响应向量，freduced为缩聚点上的等效气动力，该气动力模型即可在地面颤振模拟试验中使用，气动力模型的建立整个过程如图9所示。

(20)

图8 基于缩聚点插值后振型与原始振型对比Fig.8 Comparison between modal shape interpolated from condensed nodes and original shape

图9 物理坐标下气动力建模流程Fig.9 Aerodynamic modeling process in physical coordinates

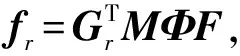
表3 坐标变换及插值点缩聚精度分析Tab.3 Analysis of accuracy for coordinate transformation and condensation of interpolation nodes

6 结构建模与仿真

为了对本文提出的气动力模型重构方法精度进行验证，利用直接耦合法计算结果作为标准，采用仿真的方式进行对比验证，以表1中Ma=0.96作为验证状态点。采用有限元计算获得的质量阵、刚度阵以及模态振型矩阵，建立了结构状态空间模型，并与气动力模型构成闭环系统模拟结构的颤振特性，通过在不同来流条件下进行测试，获得了不同测试速度条件下的系统响应情况，通过调节来流条件，使系统的响应幅值达到稳定，从而获得系统的临界稳定点，对应的测试条件即为结构的颤振边界。图10给出了亚临界(来流速度326 m/s)、临界(来流速度330 m/s)和超临界(来流速度340 m/s)，系统仿真响应输出情况。

图10 不同风速条件下系统响应(亚临界、临界、超临界)Fig.10 System response under different test condition(subcritical, critical and supercritical)

将仿真获得的颤振边界与直接耦合方法及风洞试验结果进行了对比分析(无量纲化后的结果)，三种方式获得的颤振速度边界对比情况，如图11所示。

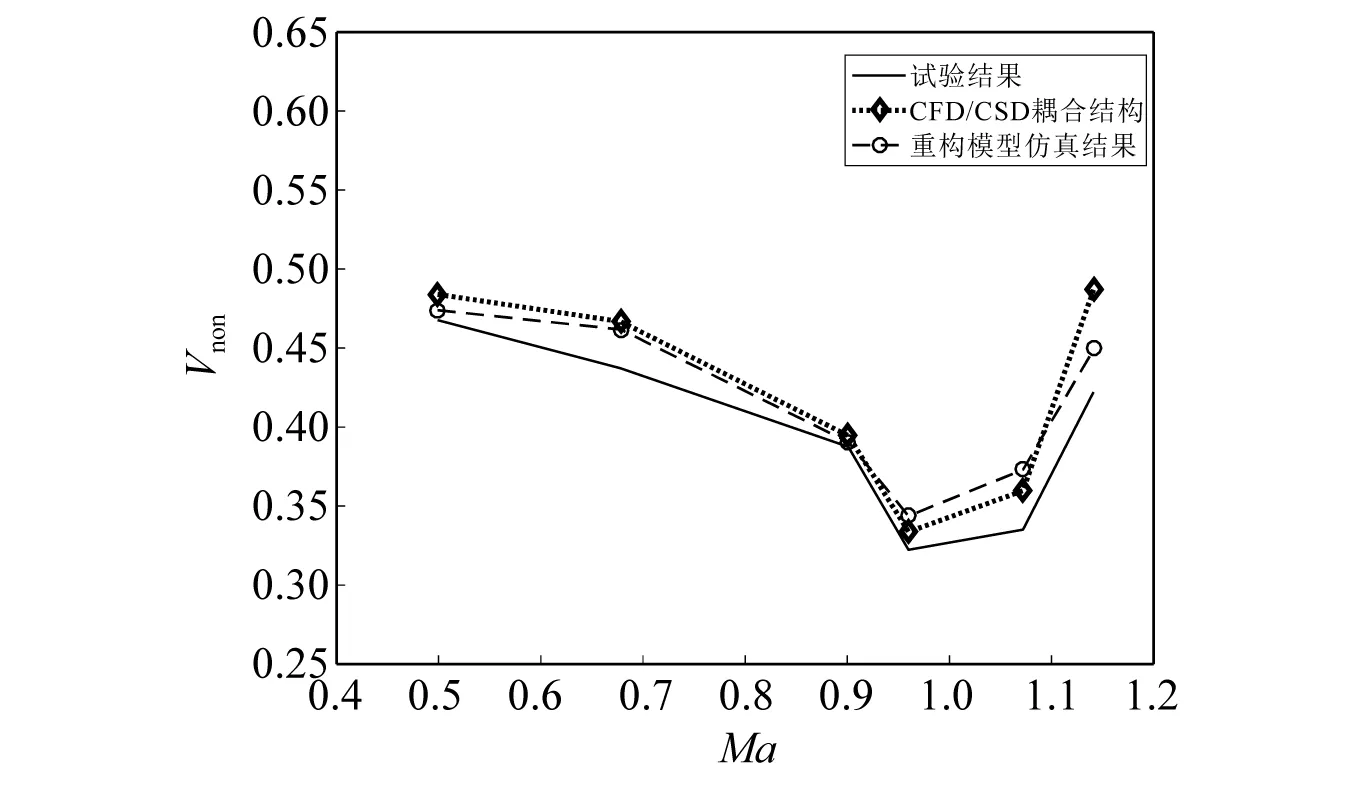
图11 颤振边界仿真结果与直接耦合及试验结果对比Fig.11 Comparison of flutter boundary simulation result with CFD/CSD coupling method and experiment

由图11可以看出，基于重构非定常气动力模型获得的颤振边界与直接耦合法获得的颤振边界吻合较好，证明了本文提出方法的有效性，同时为了验证建立的模型是否满足实时性要求，设计了半物理试验，试验采用NI半物理仿真设备，将建立的气动力模型在设备上运行，设置仿真模型采样频率为200 Hz，试验中未出现运行丢帧的情况(如果出现丢帧证明在一个采样周期内模型未能完成运算)，证明了模型的运行时长小于0.005 s，从而可以证明效率满足试验的要求。至此已经实现气动力的重构，并且模型在实时性和插值点数量方面均满足地面颤振模拟试验的要求。

7 结 论

本文依据地面颤振模拟试验对非定常气动力模型的要求，提出了一种基于CFD降阶模型的非定常气动力重构方法，建立了模态坐标下的非定常气动力模型。通过提出的坐标变换方法将气动力模型转换至物理坐标下，采用标准模型AGARD445.6作为验证对象，基于建立的结构模型进行了联合仿真证实了提出方法的精度和有效性，具体结论入如下：

(1) 引入了气动力降阶模型方法，基于CFD技术建立了广义坐标系下的气动力影响系数矩阵，提高了气动力计算效率。

(2) 提出了模态坐标与物理坐标量之间的转换关系，将气动力模型转换至物理坐标下，避免了不完备模态振型矩阵直接求逆带来的精度损失，提高了坐标变换的精度。

(3) 以AGARD445.6标准模型对气动力重构方法进行了验证，证明了提出的降阶重构方法在保证气动力精度损失较小的情况下，提高气动力计算的效率，满足地面颤振模拟试验对气动力模型计算实时性的要求。