基于多元智能的数学校本选修课程“四步”实施

【摘 要】 数学校本选修课程作为国家课程的拓展与补充,没有高考压力,在课程实施过程中内部动机起着更为主导的作用,学生的多元优势智能得到更大程度的发挥.以《数学多棱镜》第四章中“探秘经典”单元—课时教学为例,通过“努力触发燃点线”“精心打造共同体”“细致滋养生长点”“缤纷绚烂展示群”的“四步”课程实施,让学生对“基本不等式”与“柯西不等式”的悠久历史、相互关联、几何背景、代数诠释、思想启示进行深入探究,在此过程中学生的多元优势智能助推数理逻辑智能,推动学生的数学探究活动.
【关键词】 校本选修;多元智能;“四步”实施;探秘经典
1 问题缘起
数学校本选修课程作为国家课程的拓展与补充,其实施过程是以国家课程的实施为基本蓝图,但是又较之国家课程有学生更为广阔的发挥发展空间,因为数学校本选修课程的实施更为自由灵活机动.国家课程以高考影响下的成绩目标为导向,对于学生来讲有很强的外部动机,而校本选修课程没有高考的压力,学生的表现更随心而动,内部动机起着更为主导的作用.在课程实施过程中,学生潜藏的多元智能得到更大程度的开发,用学生各种优势智能助推数理逻辑智能,引导学生用数学的眼光观察世界,用数学的思维思考世界,用数学的语言描述世界.
2 多元智能理论基础
霍华德加德纳认为人的智能是一个复杂的综合体,涵盖语言智能、空间视觉智能、运动智能、音乐智能、数理逻辑智能、人际关系智能、自我认知智能、自然观察者(博物学家)智能、存在智能.就智能的发展问题,加德纳认为各种智能的发展存在不同的规律,但从整体而言主要有以下几点:(1)对于某一个人来说,智能的发展是不平衡的.即每个人都有各自的智能强项和弱项.智能之间的不同组合表现出个体间的智能差异,即每个人都有自己的智能轮廓;(2)智能的发展受教育和文化环境的影响很大.通过教育培养可以提高人的智能,即人的多元智能发展水平的高低关键在于后天的开发;(3)不同智能显现出来的年龄存在明显差异,应有意识捕捉不同智能发展的最佳时机;(4)不同智能之间存在相互影响,如“瓶颈效应”“补偿效应”“催化效应”.
3 《数学多棱镜》的“四步”课程实施
笔者基于多元智能理论开发的校本选修课程命名为《数学多棱镜》,之所以命名为《数学多棱镜》,是因为笔者将课程分为“数海觅踪,学无止境,多思古今,棱角分明,镜像万千”五部分,每部分的课程各具特色.“数海觅踪”侧重对国家课程里的内容二次挖掘;“学无止境”侧重学生的奇思妙想;“多思古今”侧重从数学史的角度探究高中数学中的某些内容;“棱角分明”侧重对经典公式定理的来龙去脉进行探究;“镜像万千”侧重数学与实际生活的紧密联系.综合基于多元智能的校本选修课程实施可以分为“四步”:点燃、构建、深潜、共享.下面笔者以第四章中“探秘经典”的单元—课时教学为例,谈谈数学校本选修课程的“四步”实施.
3.1 点燃:努力触发燃点线
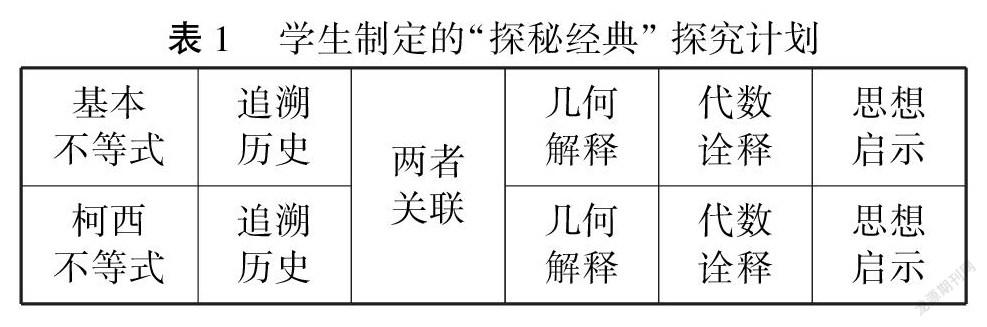
在一般的数学学习中,学生的数学学习往往是被教师提出的问题或任务驱动,而笔者追求的校本选修课程在实施过程中,希望由学生自主自发地发现问题.提出一个问题往往比解决一个问题更重要,因为解决问题也许仅是一个技能而已,而提出新的问题、新的可能性或者从新的角度去看旧的问题,却需要有创造性的想象力,而且标志着科学的真正进步.在“探秘经典”课程实施的起始阶段,笔者意图让学生自己寻找感兴趣并且想探究的问题.数学中有很多经典的公式、定理、不等式与性质等,所谓的“经典”,可以从不同角度诠释,学生心目中的“经典”有他们自己的诠释.教师设计问卷调查学生心目中的“经典”,统计结果表明学生对“经典不等式”感兴趣,因此笔者就将“经典”定位在不等式的研究上.进而笔者让学生选择心目的“经典不等式”,很多学生都选择“基本不等式”和“柯西不等式”,于是让学生自己制定研究计划,点燃探究火花,触发思维燃点线.学生通过讨论达成共识,制定了以下的研究计划,尽可能全面揭示“基本不等式”与“柯西不等式”的经典之处.
学生对于制定这样的探究计划给出了自己的理由:首先这两个不等式之所以经典因其具有深厚的历史底蕴,其次它们的经典之处表现为“经典”与“经典”之间往往存在千丝万缕的联系,再次它们的经典之处应该体现为具有非常好的“数形结合”属性,最后它们的经典之处在于蕴含在其中的思想方法具有推广价值与意义.燃点线的触发与研究计划的制定是一个调动学生自我认知智能与人际关系智能的过程,当然数理逻辑智能依然占据主导地位,而其他智能对数理逻辑智能的辅助与助推作用也显得尤为关键.3.2 构建:精心打造共同体
从高考的角度看,数学需要独立思考,因此在国家课程的实施过程中,教师更多地是鼓励学生对问题进行独立思考和自主探究.但从辩证角度看,事物总有两方面,如果片面地强调独立思考,容易闭门造车或出现“当局者迷”的情况,从某种程度上限制了学生多元智能发展的空间.作为国家课程补充的校本选修课程没有高考压力,可以充分发挥数学学习共同体的强大功能.精心打造的学习共同体要体现“同组异质”.从智能角度讲就是同组的學生尽量拥有不同的优势智能,这样的学习共同体具有两种基本功能:(1)社会强化:建立学习共同体是满足学习者的自尊和归属感需要的重要途径,这里的自尊与归属感也体现在智能的自尊与归属感;(2)信息交流:学习者与辅导者进行交流,同时又与同伴进行交流和合作,共同建构知识、分享知识、智能互补.
在“探秘经典”实施过程中,学习共同体内部均进行了不同程度的分工,综合起来基本都是按照学生的智能优势进行分工.拥有语言优势智能的学生侧重挖掘与查询历史渊源,拥有自然观察者优势智能的学生侧重研究两者的关联,拥有空间视觉智能优势的学生侧重研究几何解释,拥有数理逻辑优势智能的学生侧重研究代数诠释,拥有自我认知优势智能的学生侧重研究思想启示,而拥有人际关系优势智能的学生负责综合各类研究,与众人磨合,形成展示成果,最终进行汇报的人员可以是拥有数理逻辑优势智能与语言优势智能的“组合”.
3.3 深潜:细致滋养生长点
针对學生制定的研究计划和共同体分工,笔者为学生的研究活动滋养几个生长点,让学生的数学思维、素养伴随着多元智能经历顿悟、破土而出.3.3.1 经典之“中西方数学发展的比较”
中西方数学文化有着各具特色的发展历史与特征,我国古代数学拥有璀璨的文化,值得学生去追溯,比较中西方关于两个经典不等式的研究特色与区别.
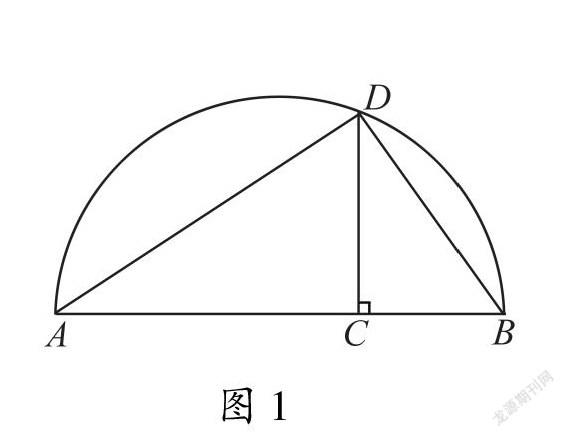
(1)基本不等式西方对于基本不等式的研究比较早,公元前6世纪,毕达哥拉斯学派已经知道算术中项、几何中项以及调和中项,毕氏学派的哲学家阿契塔在《论音乐》中定义了上述三类中项,并把几何中项小于等于算术中项叫做基本不等式.欧几里得在《几何原本》中给出了两条已知线段之间的几何中项的作图方法,如图1所示,以AB为直径作半圆ADB,则CD即为AC和CB之间的几何中项.欧几里得之后,芝诺多鲁斯在《论等周图形》中给出命题:在边数相同、周长相等的所有多边形中,等边且等角的多边形的面积最大.在四边形中便可以得到基本不等式.
我国对于基本不等式的研究最经典的首推“赵爽弦图”(如图2所示),赵爽是公元3世纪三国时期东吴的数学家,赵爽弦图的经典之处在于他用截、割、拼、补来证明代数式之间的恒等关系勾股定理,而“基本不等式”也蕴含于赵爽弦图中,赵爽在给《周髀算经》作注时写道:“以图考之,倍弦实,满外大方,而多黄实,即勾股差实.以差实减之,开其余,得外大方.大方之面,即勾股并也.”由此可以让学生探究得到基本不等式.
(2)柯西不等式
也许学生会认为“柯西不等式”顾名思义是由柯西首次提出的,但是如果引导学生再细细查找蛛丝马迹,便可发现两个值得斟酌的问题.其一,从历史角度讲,柯西不等式应该称为“柯西-布尼亚克夫斯基-施瓦茨不等式”,其原因值得学生追溯;其二,从我国历史角度讲,赵爽弦图的变形图(比如将赵爽弦图中的正方形换成平行四边形等)中也可以得到柯西不等式.
我国古代数学的风格是以形证数,数量关系与空间形式往往是形影不离地并肩发展着,十七世纪笛卡尔解析几何的发展正是我国这种传统思想和方法在几百年停顿后的重现和继续.不妨可以对学生进行“立德树人”的爱国主义教育:我国文化传承于儒家中庸之道,一向比较低调含蓄,而且由于年代久远,我国的很多数学研究成果未必能够完整保存下来,所以有待于我们继续去考证与发现我国古代璀璨的数学文化宝库.
3.3.2 经典之“两者间关联程度的摸索”
数学的发展告诉我们,不同的数学知识之间存在千丝万缕的联系,也正是这种联系推动数学不断的发展,学生相信“基本不等式”与“柯西不等式”两大经典不等式之间也存在必然的联系.学生发现,对于二维柯西不等式(a2+b2)(c2+d2)≥(ac+bd)2,如果取c=d=1时,二维柯西不等式就是二维基本不等式a2+b2≥2ab;而对于三维柯西不等式(a21+a22+a23)(b21+b22+b23)≥(a1b1+a2b2+a3b3)2,如果取b1=b2=b3=1,三维柯西不等式就是基本不等式的变形a21+a22+a23≥a1a2+a2a3+a3a1;如果继续将柯西不等式推广到n维,依然可以找到与基本不等式之间的关联.
数学之间的关联不仅仅体现在两个经典不等式横向之间,也体现在两个经典不等式与不同知识内容之间.两个经典不等式原本属于代数领域研究的内容,但是它们与其他代数领域的内容、几何领域的内容都存在关联,因此就有了以下两个“经典”:几何背景与代数观点.3.3.3 经典之“多角度几何背景的探究”
基本不等式与柯西不等式具有丰富的几何背景,单从我国古代数学看,两个不等式都可以与优美几何图形紧密相连.随着几何学的深入学习,学生知道向量、复数都有几何诠释,还有完美体现数形结合的解析几何,因此两个经典不等式与向量、复数、解析几何都有深刻的关联.比如图3所示,设平面直角坐标系中两点A(a1,a2),B(b1,b2),则a=OA=(a1,a2),b=OB=(b1,b2),OD是O到直线BD的垂线段,OB是O到直线BD的斜线段,二维柯西不等式的一种几何背景是:定点O到直线BD的垂线段OD比斜线段OB更短\[1\].3.3.4 经典之“统一性代数观点的整合”
从代数观点看两个经典不等式也可以是多角度的整合,可以从不等式作差的角度、复数集内的三角不等式角度、方程的角度、函数的角度,而不等式、方程、函数三者之间又存在重要关联,这也是高中数学着重要研究和考查的内容之一,显示出数学内部的和谐美与统一美.比如基本不等式与对勾函数的紧密联系,而柯西不等式与某一个一元二次方程的判别式存在关联,而且可以推广到n维柯西不等式,从代数观点,柯西不等式源于平方式非负的性质,这与几何中距离非负相对应.3.3.5 经典之“合理化思想方法的推广”
既然两个经典不等式有着如此悠久的历史,有着如此默契的关联,有着如此丰富的几何背景,有着如此深刻的代数诠释,那么我们不仅能够运用这两个经典不等式解决很多的问题,而且能够将蕴含其中的思想方法在解决问题上进行推广应用,比如构造平面图形解决问题,构造空间图形解决问题,构造解析几何图形解决问题,构造函数解决问题,构造复数解决问题,构造向量解决问题等.3.4 共享:缤纷绚烂展示群
展示是校本选修课程实施的一个重要环节,经过学习共同体对两个经典不等式的“深潜”,均有所斩获,通过学习共同体的书面汇报,笔者发现,由于不同的学习共同体的主导优势智能有所不同,因此探究侧重点也会有所不同,探究的深浅程度也有所不同.笔者根据不同学习共同体的优势与特点帮助他们选择合适的展示点,由此形成缤纷绚烂的展示群.
通过展示,学生的多元智能得到可视化的体现,让共同体内的每一位学生的自我价值都得到体现;通过展示,学习共同体内部遗留的问题可以得到不同视角的释疑,让学习共同体走出固步自封的象牙塔,产生豁然开朗的顿悟;通过展示,会闪耀出教师意想不到的亮点,让学生们惊叹于“原来如此”,折服于同伴的智慧,充分印证了学生惊人的想象力与敏锐的观察力;通过展示,汇聚成学生的过程作品集,这是学生多元智能相互推动的成果,记录团队精诚合作的历程,形成学生深度学习的智慧结晶.
参考文献
[1] 李尚志.柯西不等式之几何白话版\[J\].高中数学教与学,2021(07):41-43.
作者简介 俞昕(1977—),女,浙江湖州人,正高级教师,硕士;主要研究数学文化、数学校本课程、多元智能等;有多篇论文发表.

