状态/输入约束下飞-推一体化的保性能安全控制

马悦萌，周 荻，邹昕光

(1.哈尔滨工业大学航天学院，哈尔滨 150001；2.哈尔滨工业大学电子与信息工程学院，哈尔滨 150001)

0 引 言

吸气式高超声速飞行器(Air-breathing hypersonic vehicle,AHV)有全球快速打击、超音速低空突防、低成本空天运输等优点，因此有重大的军事与经济价值。为使其得到更好的发展，必须解决好控制一体化设计、高超声速空气动力学、高性能动力推进等技术难点。

吸气式高超声速飞行器机身前体作为进气道的预压缩面，为燃烧室提供具有合适温度、压力、马赫数和流速的均匀流场；机身后体作为发动机尾喷管的一部分，使燃烧反应产生的高温高压气流作用于AHV后体下表面，产生推力、附加升力和力矩。AHV模型最重要的特点是空气动力系统和推进系统之间的强耦合作用，需要考虑进行飞行推力控制系统的综合设计。

近年来，由于高超声速飞行器模型具有非仿射非线性以及参数摄动等特性，backstepping与自适应控制和智能控制相结合的算法被广泛应用于AHV的控制器设计。针对输入受限的未知奇异摄动系统，Fu等提出了一种基于Lyapunov函数的多时间尺度动态神经网络观测器来估计系统的状态，并设计了考虑输入约束的自适应最优控制器，可以克服执行机构的饱和限制。Bu等在此基础上针对吸气式高超声速飞行器的非仿射模型，设计了一种新型反演鲁棒自适应跟踪控制器；通过神经网络逼近来估计未知的非仿射动态，保证了所设计控制系统的鲁棒性。针对一类含有未建模动态的随机非线性切换系统，Li等使用模糊逻辑来识别完全未知的非线性系统函数，并基于Lyapunov理论与小增益定理，提出一种新型鲁棒自适应模糊反演镇定控制策略。进一步，Sun等提出了基于输出反馈的、有限时间收敛的自适应模糊非光滑反演控制方案，证明了基于模糊层次分析法设计的观测器估计误差会在固定时间内收敛，与初始估计误差无关。

当超燃冲压发动机不起动时，其进气口外会受到一个法向冲击，在飞行器前部诱发抬头附加力矩，该力矩会对飞行器的静稳定性产生影响，造成控制系统失效，在AHV控制中应尽量避免出现发动机不起动现象。对超燃冲压发动机而言，造成不起动的主要原因是发动机进气情况恶化，无法为燃烧室提供利于燃料燃烧的均匀流场。而由于AHV的一体化布局，进气道的进气情况与飞行器速度与攻角息息相关，因此为保障AHV飞行的安全性，飞行器自动驾驶仪的设计中速度与攻角约束需着重考虑。

An等综合考虑不确定性参数与进气道不起动条件，设计了一种有性能保证的容错控制器，使用特定性能函数对攻角与速度进行了相关约束，以保证超燃冲压发动机有较好的进气条件。Bu等基于backstepping方法针对一类不确定性非线性动力学系统设计了一种预定性能控制器，通过定义一系列转换误差，将有约束的系统转换为无约束系统进行控制器设计，保证了输出跟踪具有小甚至零超调。Guo等将这种性能约束方法应用于高超声速飞行器执行机构滞后与攻角约束问题，将执行机构滞后视作有效性能丧失与有界干扰的组合，构造自适应补偿率对其进行补偿，并使用预定性能控制器保证了对攻角的约束。进一步，丁一波等针对吸气式高超声速飞行器的瞬态性能与发动机进气攻角约束问题，设计了新型设定时间预定性能边界函数，可以通过调整该函数的初始收敛速率来避免控制信号饱和，性能边界对攻角的限制满足了发动机的进气需求。同样针对AHV实际飞行过程中执行器饱和的问题，刘田禾等建立了带有执行器饱和的切换系统模型，并给出了基于线性矩阵不等式设计方法的抗饱和切换控制器。

由于超燃冲压发动机工作条件苛刻，为防止执行机构故障引发事故，一些学者将注意力转向容错控制算法。He等针对存在参数不确定性、执行器故障和外界干扰的AHV控制问题，提出一种自适应输出反馈容错控制器；并设计了能在被控对象参数、执行器故障参数均未知的情况下自主更新控制器参数的自适应律。Peng等提出一种基于障碍Lyapunov函数的AHV状态约束自适应容错控制方案，可以将飞行状态约束在安全边界之内，同时针对升降舵的未知故障引入自适应容错控制进行处理。进一步，Sun等针对具有输入饱和状态约束的AHV，加入辅助系统解决了其执行机构饱和的问题。

由于高超声速飞行器与超燃冲压发动机机械上的一体化设计，受限于超燃冲压发动机苛刻的工作条件，已有的工作多集中在对飞行器状态进行限制来保证发动机的正常工作。然而这样的设计思路往往忽视了超燃冲压发动机本体模型的复杂性，简化了发动机安全问题，简单地认为发动机安全对攻角的约束是一个固定范围，这样所设计的飞行器控制系统为保证发动机安全，其姿态约束的保守性较大，影响了AHV本身的灵活机动。

在飞-推一体化设计中，本文将把超燃冲压发动机模型与飞行器模型相结合考虑，综合设计了速度通道控制器。所设计的保性能安全控制器将不会为了发动机的起动安全去一味地限制飞行状态，而是使用结构如图1所示，有前后两个轴向安装支板来供油的超燃冲压发动机，在确保发动机安全的情况下输出所需推力，同时放宽了进气条件对攻角的约束范围，极大地解放了AHV的机动灵活性。

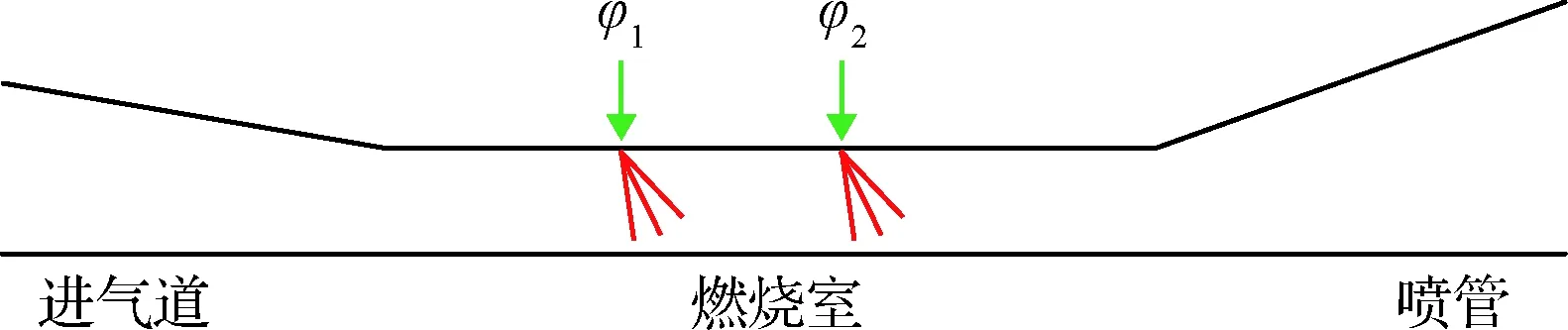
图1 超燃冲压发动机简图Fig.1 The sketch of scramjet

本文的主要贡献总结如下：

1)建立了面向控制的超燃冲压发动机安全-推力模型。相比传统研究中所使用的单一推力模型，增加了对发动机进气道安全裕度与燃烧室最高温度这两个安全状态的建模，更贴近于工程实际。

2)基于本文所建立的速度通道一体化模型，设计了具有温度约束、进气道稳定裕度约束的AHV控制系统；并基于障碍Lyapunov理论进行了稳定性证明，从理论上保证了AHV飞行全过程发动机安全状态不越界。扩张状态观测器与自适应算法被用来提高控制系统的鲁棒性，辅助系统用于让执行机构尽快地退出饱和状态。

1 AHV数学模型

本研究中涉及的吸气式高超声速飞行器纵向动力学模型采用目前高超声速飞行器控制系统研究应用较为广泛的Parker飞行器模型，见式(1)～(4)。

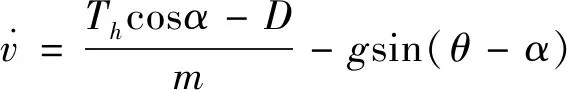
(1)

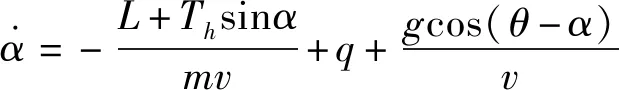
(2)

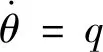
(3)

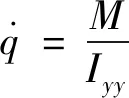
(4)

其中，,,,,分别为飞行器的质量、速度、攻角、俯仰角与俯仰角速率；,,分别为飞行器所受到的升力、阻力与俯仰力矩;为超燃冲压发动机推力；,分别为当地重力加速度与俯仰转动惯量。乘波体模型的空气动力学解算及其与推力系统的耦合分析参考文献[18]。

吸气式高超声速飞行器飞行过程中系统状态会涉及工作边界问题。比如，在空气动力方面，飞行器攻角的约束不仅用以维持飞行器姿态，而且也保证了正常的发动机进气道波系结构与捕获流量；进气道激波串安全约束使得燃料可以稳定燃烧，同时防止发动机出现进气道不起动现象；燃油当量比约束保证了燃料的稳定燃烧，在防止发动机热滞熄火的同时也提高了燃料的利用效率；燃烧室最高温度约束保证了飞行器结构的安全，防止过温产生的材料、结构变形问题。在如此繁多的约束下，吸气式高超声速飞行器的控制系统设计是一个复杂的非线性、强耦合、多变量、多约束的控制优化问题。

由于鲜少有文献针对AHV中超燃冲压发动机进行完整的安全-推力建模，本文选取文献[19]中的碳氢化合物超燃冲压发动机为研究对象，在现有的计算流体动力(Computation fluid dynamics,CFD)模型基础上，使用面向控制的多项式模型对超燃冲压发动机进行最小二乘拟合，并结合已有的超燃冲压发动机理论研究成果，将发动机内部机理传递过程补充为发动机模型的动态环节，最后该模型将用于本文飞-推一体化的保性能安全控制器的设计。

由上述分析，吸气式高超声速飞行器所搭载的超燃冲压发动机其安全-推力模型所关注的状态共有三个，分别是进气道安全裕度、燃烧室最高温度与输出推力。前两个状态的建模是为了针对其模型分析设计控制器以保证超燃冲压发动机的起动、结构安全性，推力模型是为了保证发动机的输出性能。

根据文献[18]中对超燃冲压发动机的机理分析以及控制系统设计方面的考量，用于拟合的多项式模型如式(5)所示。

=++++++

+++

(5)

式中：为飞行器飞行攻角,为发动机轴向前端支板供油的燃油当量比，为发动机轴向后端支板供油的燃油当量比。

同理给出进气道安全裕度与燃烧室最高温度的拟合模型如式(7)～(8)所示。进气道安全裕度通过超燃冲压发动机反馈的燃烧室背压信号和进气道最大背压信号来定义，见式(6)。

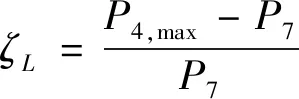
(6)

=++++++

+++

(7)

=++++++

+++

(8)

由于三维拟合较为困难也不利于拟合效果的可视化，因此本文先分别进行两个二维拟合，再对两个二维拟合的结果进行融合来逼近发动机的真实模型。式(5)～(8)所示的多项式模型中，控制输入,的最高次项都是一次，而可以达到三次，这样的设置一方面是从控制器设计考虑，希望拟合模型为仿射系统；另一方面，通过CFD数据与真实发动机模型的特性，发现增高控制输入,的阶次后，其减小拟合残差的效果并不明显，而过高输入阶次的模型对控制器的设计与实现将提出挑战，因此权衡各方因素后选择了式(5)～(8)。

1.1 发动机安全-推力二维模型拟合

本节将以推力模型为例说明进行二维拟合的过程，其余两个安全模型的拟合可类比推力模型，过程基本相同。

将式(5)分解为两个二阶模型的组合，见式(9)。

=((,),(,))

(9)

(,)=+++++

+

(10)

(,)=+++++

+

(11)

式中：为两个二维模型的融合函数，,分别为两个二维拟合所得到的三次多项式模型。

采用最小二乘法对式(10)～(11)进行拟合，可得其拟合参数。的拟合残差见图2，在燃油当量比与攻角濒临边界时，拟合效果出现较大误差，这是因为此时发动机已处于安全边界，性能急剧下降，安全裕度急剧减小，三阶多项式关系不足以描述这种恶化特性，从而出现较大的拟合误差。本文所设计的控制系统将把发动机状态严格限制在安全范围内，不会让发动机工作在性能恶化的边界点上，因此这部分大误差的发动机特性对面向控制器设计的模型来讲,危害不大,可以容忍。

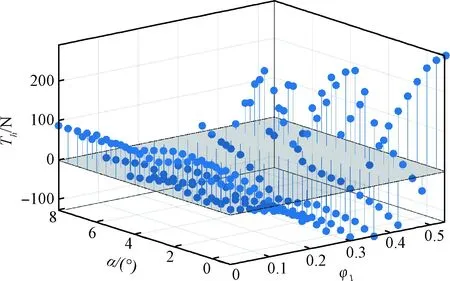
图2 推力f1拟合残差图Fig.2 Residual diagram of f1 thrust fitting

1.2 发动机安全-推力模型的融合与验证

1.1节中所得的与中均含有攻角项，将两个模型简单相加所得的融合模型对于攻角的拟合必然会存在较大的误差。针对这一问题，采用拟合误差反馈的思想对融合模型进行循环拟合逼近，将简单相加所得到的模型作为fit_model的迭代初始值。

具体实现方法如下：(初始=0)

1)前后两支板燃油当量比,随机选取50个点，而攻角按照从小到大等步长选取覆盖范围为[-1,8]的50个点；

2)将这些点分别输入fit_model和CFD模型中，得到两个模型的输出，判断拟合残差是否符合建模精度要求，若符合则退出循环进入第4步，否则=+1并进行第3步；

3)选取CFD输出与fit_model模型输出之差作为新的待拟合变量，选取攻角的阶多项式进行拟合，并将拟合结果记为offset项加在fit_model模型中，并回到第1步重新采样评估；

4)最终对,,均随即抓取50个点判断拟合残差是否符合要求，符合则输出最终模型作为面向控制的超燃冲压发动机模型，否则重新回到第1步。上述算法的流程见图3。

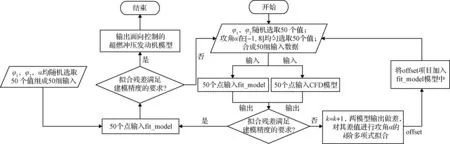
图3 发动机安全-推力二维模型融合与验证流程图Fig.3 Flow chart of scramjet safety-thrust 2D model fusion and verification

采用拟合误差反馈的思想对总模型进行循环拟合逼近后，符合残差要求(max:10%)的系统模型参数见表1～3。

表1 推力模型拟合参数数值Table 1 Parameter fitting table of thrust

推力的拟合效果见图4，其最大拟合误差为3.157%，与推力类似，发动机进气道安全裕度模型拟合最大误差为8.927%，燃烧室最高温度模型拟合最大误差仅有0.528%。可见通过本节算法所得到的拟合修正模型可以较好地体现超燃冲压发动机的安全工作特性。

图4 发动机推力拟合效果图Fig.4 Fitting result diagram of thrust

2 AHV速度通道控制系统设计

2.1 安全子系统控制器设计

..进气道安全裕度对控制输入的约束分析

进气道安全问题主要危害表现为进气条件恶化导致激波串从前端被推出隔离段,从而引起发动机进气量极度下降的不起动现象。式(6)为发动机建模中较为常用的一种进气道安全裕度定义，形式简单,含义清晰，本节基于对1.2节中所建进气道安全裕度模型的分析，设计控制约束以确保发动机的进气安全。

如果激波串从前端被推出隔离段，AHV将出现发动机不起动问题。为了避免出现不起动现象，观察进气道稳定裕度多项式稳态模型，不难发现其与控制输入关系极大，并且由于供油所产生的爆炸可以有效地隔离供油爆炸对进气道端的压力，因此对进气道安全裕度几乎无影响，这点从表2的拟合系数上也有所体现，即相关项的拟合系数绝对值远小于。控制中可以直接忽略与相关的绝对小项，简化为式(12)所示模型，由该表达式知，只要得知飞行器当前攻角，限制控制输入的大小，便可以将进气道安全裕度限制在一个安全范围内。

表2 进气道稳定裕度模型拟合参数数值Table 2 Parameter fitting table of inlet stability margin

++

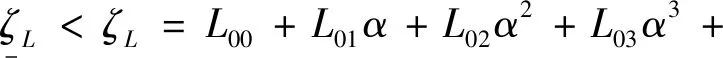
(12)

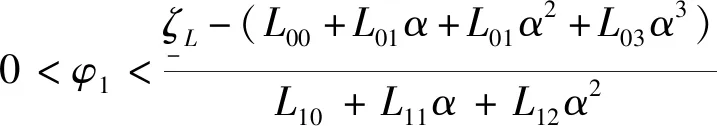
(13)

根据表2的模型拟合参数，忽略绝对值小的参数值，得到最终用于控制器设计的取值范围为式(14)，这个范围将作为执行机构的饱和限制以保证超燃冲压发动机的起动安全。

(14)

根据燃油当量比本身的饱和限制，即0<+<11(保证氧气足够让燃料充分燃烧)可知系统另一个执行机构的饱和限制见式(15)。

0<<11-

(15)

需要注意的是式(14)与式(15)所示的饱和界都是一个动态值，与飞行器攻角、飞行高度与飞行速度有关，根据飞行条件的不同将会实时更新。为了防止控制输入,长时间处于饱和状态，将在控制器设计时加入辅助系统来加速退饱和。

至此，对于面向飞-推一体化的AHV所搭载超燃冲压发动机的两个控制输入，其饱和限制已经由进气道安全裕度与燃油当量比约束确定完毕。

..最高温度控制子系统的设计与稳定性证明

过高的燃烧室温度不仅会破坏超燃冲压发动机的材料与结构，还可能会使燃料在进入燃烧室前便焦糊，因此燃烧室内的最高温度控制对发动机的安全至关重要。本文针对1.2节中建立的燃烧室最高温度模型，基于障碍Lyapunov理论设计了有状态约束的抗饱和鲁棒自适应控制器，从理论上保证了燃烧室最高温度在飞行全程均不会触碰到安全边界。

1.2节中拟合的发动机燃烧室最高温度多项式模型为一个稳态模型，这里加入一个一阶惯性环节模拟温度的动态传播过程,依据超燃冲压发动机的机理分析选取动态过程的过渡时间为。再根据表3的模型拟合参数，忽略绝对值小的参数值，这时超燃冲压发动机的微分方程模型如式(16)所示。在超燃冲压发动机内，支板供油燃烧所引发的燃烧室温升高，因此这里将看为最高温度子系统的控制输入，则看为复合扰动的一部分。

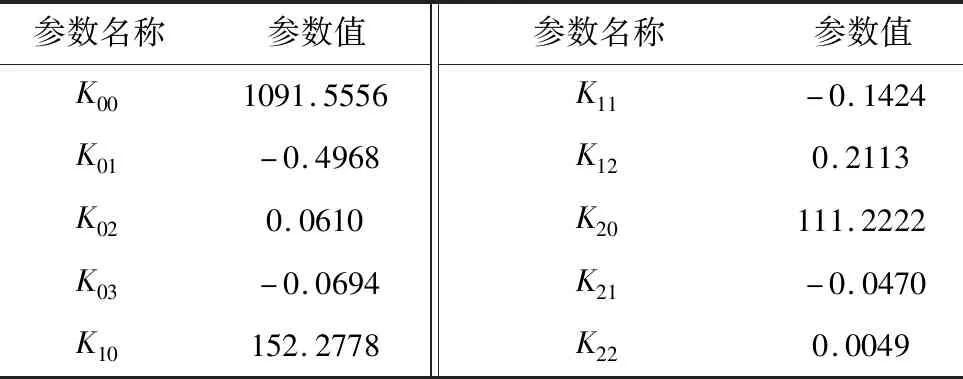
表3 燃烧室最高温度模型拟合参数数值Table 3 Parameter fitting table of the max temperature in combustion chamber

(16)

定义燃烧室最高温度子系统中的复合扰动如式(17)所示，并采用自适应算法对复合扰动的上界进行估计。

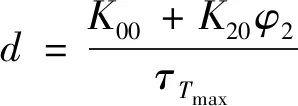
(17)

由于控制输入有式(14)所示的饱和约束，使用式(18)所示的输入带有饱和函数的模型代替原模型来体现这一约束。温度子系统的控制输入=，忽略喷油阀的动特性，则有=，考虑的饱和约束有=sat()。

(18)

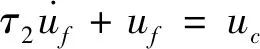
由于饱和约束=sat(2)，因此是有界的，则显然是一个有界的复合干扰，这一点对后续Lyapunov稳定性证明至关重要。

(19)

设误差状态=--，其中是温度指令，本文将在仿真校验部分给出一个温度指令生成系统，该系统能够根据推力指令给出一个相适应的温度指令;为退饱和辅助系统的状态变量,并有

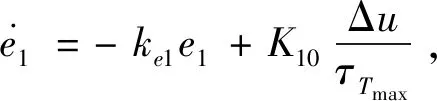
式中：Δ=-，1为辅助系统的可调参数，通过改变1的大小可调整控制输入的退饱和速度。

对求导得

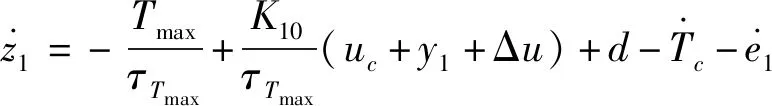
(20)

温度控制子系统对超燃冲压发动机而言是一个安全性的控制，因此除了跟踪指令外，还要保证控制的全过程中系统状态不可以超过容许温度上界，这里采用障碍Lyapunov理论来处理这一问题。

设对数型障碍Lyapunov函数为

(21)

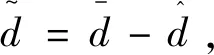
估计式(17)所示复合干扰的自适应估计算法为式(22)，其中与是自适应算法的可调参数。

(22)

设计燃烧室最高温度子系统的控制律为

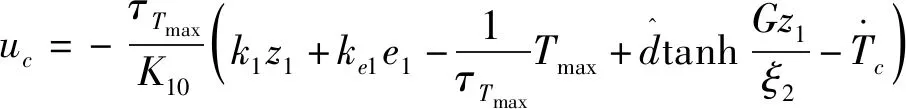
(23)

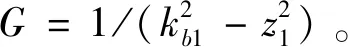
对式(21)求导并代入式(23)、(20)、(22)得式(24)。

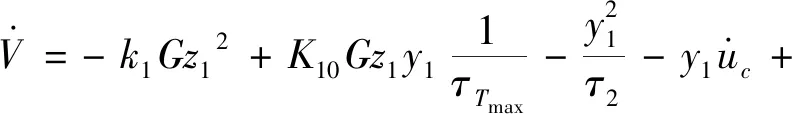
(24)

由Young不等式，知有如下三个不等式成立

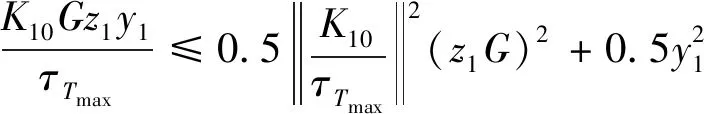
(25)

(26)

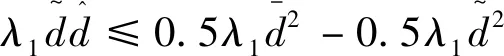
(27)

为了后续的稳定性证明，给出如下两个引理：

对于任意常数和∈R，双曲正切函数有如下不等式成立

(28)

对于任意的||<，均有如下不等式成立

(29)

由引理1可知，式(30)成立。

(30)

将不等式(30)代入式(24)，得式(31)。

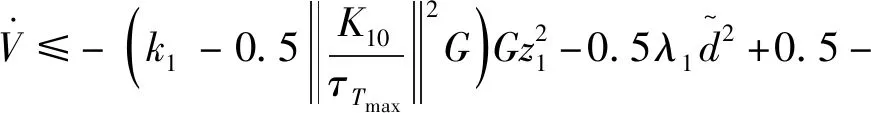
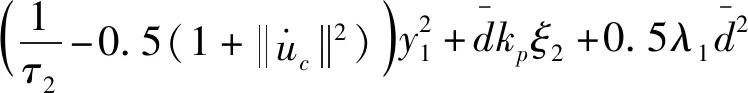
(31)

当控制参数的选取符合式(32)～(34)所示约束时，则有式(35)成立。

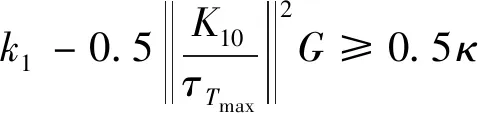
(32)

(33)

≥

(34)

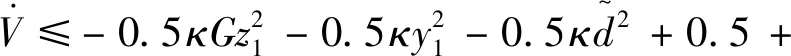
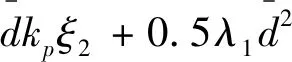
(35)

由引理2可将式(35)放缩为式(36)。

-+

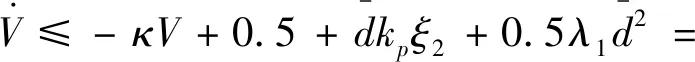
(36)

那么根据非线性系统Lyapunov稳定性理论有定理1成立。

当选择合适的控制参数满足式(32)～(34)所示约束时，该闭环系统具有如下性质：

1)闭环系统中的状态,,均是有界的；

2)误差状态满足约束条件||≤1。

由式(36)知，式(37)成立

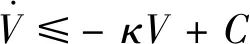
(37)

根据比较原理与式(37)，可得的时域表达式有式(38)所示的不等式成立。

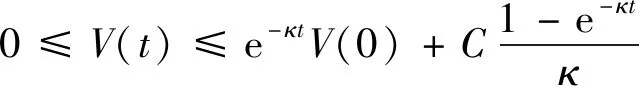
(38)

由式(38)与式(21)知，式(39)成立。

(39)

求解式(39)所示不等式可知有界，且其界如式(40)所示，通过调整参数,可使最终的约束上界稳态达到任意小。

(40)

2.2 性能子系统控制器设计

通过拟合所得到的推力模型是一个稳态模型，此处加入一个一阶惯性环节来模拟发动机推力的动态特性。认为飞行器攻角是在±10°内变化的小量，对式(1)进行简化，联合1.2节中所建的推力模型可得式(41)～(42)所示的速度-推力控制子系统微分方程模型。本节将作为性能子系统的控制输入，看似会降低燃料利用效率，但实质上由于复合干扰中已存在所提供推力，性能子系统中用一个非线性扩张状态观测器(NESO)对其进行观测，并在的控制律中进行补偿，这种控制思路下的主要作用是补全指令所需推力。

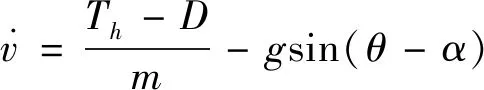
(41)

(42)

式中：(,,)=++++++++,为超燃冲压发动机推力动态过程的过渡时间,将依据其机理分析进行选取。

对于二阶的被控对象，本文采用动态面法来进行非线性控制器的设计。对于推力子系统控制输入的饱和限制，设计了辅助系统来退饱和；为了提高系统的鲁棒性，设计了NESO对系统的复合干扰进行在线观测补偿。

该性能子系统在速度闭环后，将向内环(推力回路)输入一个指令，推力回路闭环使发动机输出指令所需推力。发动机作为内回路闭环时不仅根据推力指令控制，还会根据推力指令生成一个相适应的温度控制指令控制，以求在保证发动机安全的前提下达到尽可能高的使用率，提高发动机的整体燃料利用效率。

设=,=,=1,=，得速度通道的性能控制模型如式(43)～(44)所示。设性能子系统的控制输入=，暂时忽略喷油阀的动特性，则有=，考虑其饱和约束有=sat()。

(43)

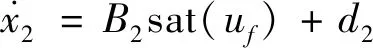
(44)

式中：两个复合干扰,定义如下

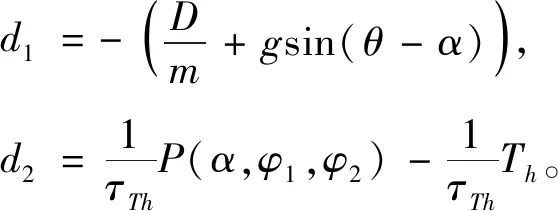
显然有界，且由于控制输入,有饱和约束，在飞行器姿态控制系统设计中也进行了状态约束，因此复合干扰也有界。

设误差状态=-=-1，其中为速度指令，对求导得

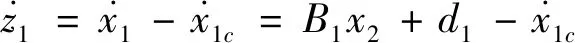
(45)

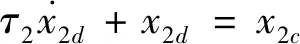
定义推力回路跟踪指令2的误差状态为=-2-，其中为退饱和辅助系统的状态变量，该退饱和辅助系统如式(46)所示。

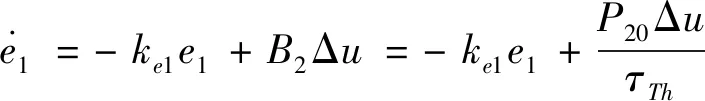
(46)

式中：Δ=-。

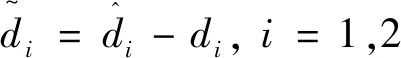
(47)

(48)

其中，(0)为函数，其具体形式见式(49)。

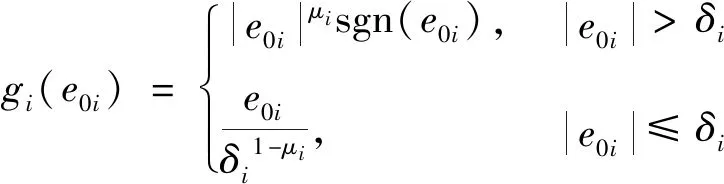
(49)

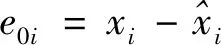
设计性能子系统外回路控制律如式(50)所示。

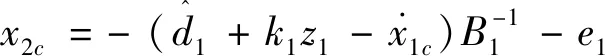
(50)

将式(50)代入式(45)得式(51)。

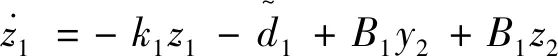
(51)

设速度回路(外回路)的Lyapunov函数如式(52)所示。

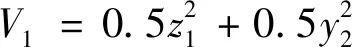
(52)

对式(52)求导并代入式(51)得式(53)。

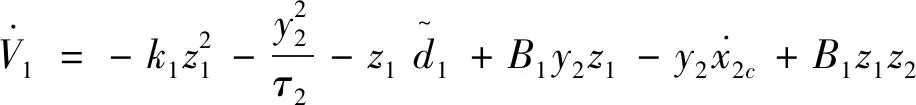
(53)

由Young不等式，有如下三个不等式成立：

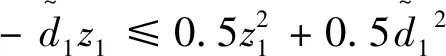
(54)

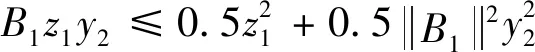
(55)

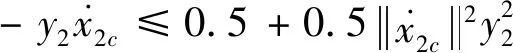
(56)

代入式(54)～(56)到式(53)中得式(57)。

(57)

下面进行推力回路(内回路)控制律的设计，对求导得式(58)。

(58)

设计推力回路控制律如式(59)所示，其中=是为了在后续稳定性分析中与中抵消的控制项。

(59)

设推力回路Lyapunov函数如式(60)所示。

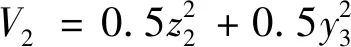
(60)

对式(60)求导并代入式(58)、(59)得式(61)。

(61)

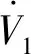
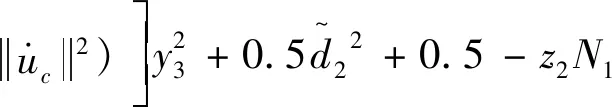
(62)

设该性能控制子系统的总Lyapunov函数如式(63)所示。

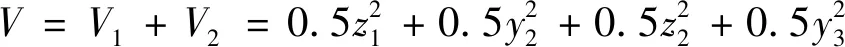
(63)

求其导数

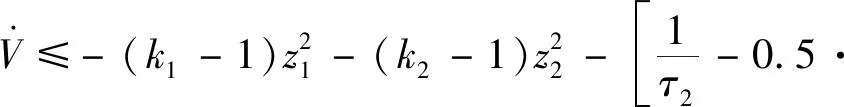
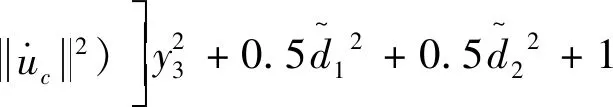
(64)

选择控制参数满足式(65)～(68)所示约束，则有式(69)成立。

-(-1)≤-05

(65)

-(-1)≤-05

(66)

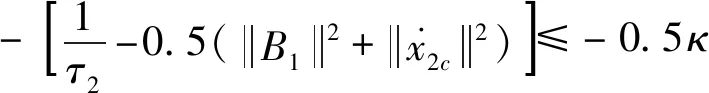
(67)

(68)

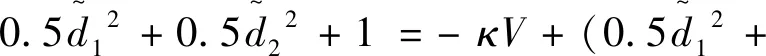
(69)

根据定理1，知误差状态,均有界，并且有式(70)成立。

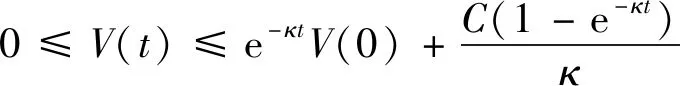
(70)

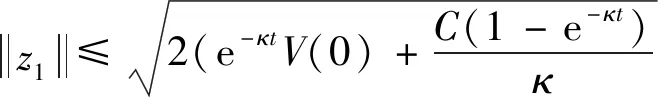
(71)

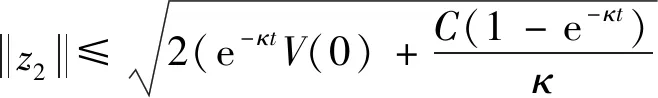
(72)

3 仿真校验

当燃烧室最高温度到达1093 ℃时，认为燃烧室过热，会造成燃烧室材料与结构的变形，危害飞行安全，因此对温度子系统误差状态进行约束，限定其合法范围如式(73)所示。温度指令的获取来源于速度控制系统解算的推力指令，其表达式见式(74)，该式是基于发动机拟合模型所推导得到的，其中饱和函数是为了保证温度控制子系统的指令不会超过1093 ℃的安全上界。

||≤1;=--;

1=1093-

(73)

=sat(900+025)

(74)

飞行器初始攻角=2.5°，初始速度=1800 m/s；让飞行器纵向通道跟踪一个大攻角指令=8°，速度通道跟踪指令=1880 m/s。飞行器姿态控制系统使用基于自抗扰理论设计的自动驾驶仪，该自动驾驶仪可以“主动”地抵抗超燃冲压发动机所带来的附加俯仰力矩，保证姿态控制系统有良好的鲁棒性能。该飞行器质量=600 kg，仿真吸气式高超声速飞行器在=24180 m的高度，速度从1800 m/s加速到1880 m/s的全过程。

将本文所设计的基于飞-推一体化的保性能安全控制器与未考虑发动机安全模型基于自抗扰控制理论(Active disturbance rejection controller,ADRC)所设计的控制器进行对比，该ADRC系统所仿真的控制策略即为只约束攻角以保证发动机进气安全的吸气式高超声速飞行器控制算法，这种控制策略下，攻角的可行安全区间往往较小，在大攻角仿真中发动机会出现安全性问题。为对比公平，用于对比的ADRC系统中NESO与本文所设计的性能子系统观测器使用同一组参数，并使用线性自抗扰反馈控制律对补偿后的系统进行闭环，控制律表达式见式(75)。

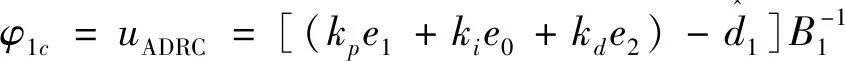
(75)

由2.1节和2.2节中的理论分析可知，本文所设计的控制系统其误差状态是有界的，并且可以根据控制参数的选取让系统的稳态误差界任意小，本节结合退保和、状态约束、控制性能等多方考虑，选择了一组合适的参数，见表4。

表4 安全-性能控制系统参数Table 4 Parameters of safety-performance control system

仿真结果如图5～11所示，实线为本文所设计安全-性能控制系统输出曲线,虚线为未考虑发动机安全模型基于自抗扰理论所设计控制系统输出曲线，点线为跟踪指令值或安全边界。

图5给出的攻角指令跟踪曲线在初始动态响应时均有一个反向的波动，这是由于当超燃冲压发动机突然起动时，飞行推力系统之间的耦合会在飞行器前部诱发附加力矩使飞行器低头。这说明发动机的开关对于俯仰力矩影响较大，对飞行器姿态稳定性有一定的危害。同理，若发动机在飞行过程中突然不起动，飞行器将受到一个较大的抬头附加力矩，该力矩会对飞行器的静稳定性产生影响。

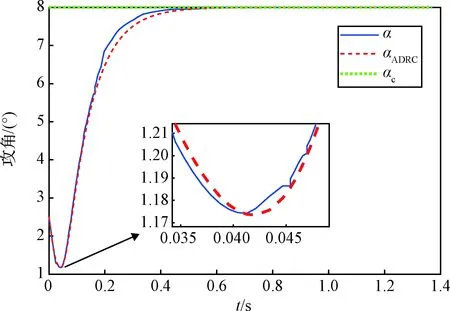
图5 AHV攻角指令跟踪曲线Fig.5 Attack angle command tracking curve of AHV

由图6知，本文所设计控制器使飞行器速度历时20 s后到达指令值，这个过程中，得益于安全子系统的存在，燃烧室最高温度保持在安全界限以内，见图8。控制器设计时，本文对进气道安全裕度进行了有效分析，对,进行了合理约束，并设计了退保和辅助系统，使发动机在飞行器加速全程安全裕度不触及危险边界，见图9。与之相比，飞行器以大攻角飞行时，ADRC系统速度指令跟踪效果并不理想，响应较慢，见图6。更为致命的是其进气道安全裕度与燃烧室最大温度均已超过安全界限，这将导致发动机熄火，燃烧室结构受损，高超声速飞行器推进系统瘫痪，见图8～9。

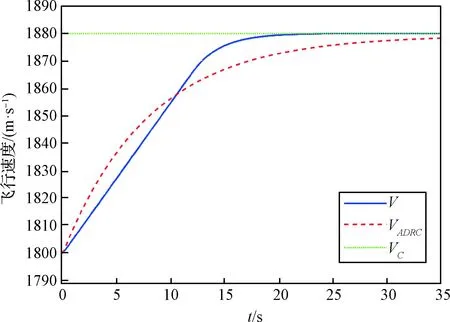
图6 AHV速度指令跟踪曲线Fig.6 Velocity command tracking curve of AHV

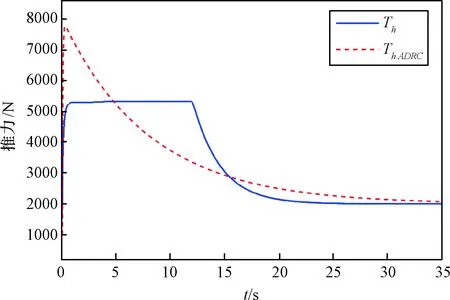
图7 超燃冲压发动机输出推力Fig.7 Thrust output of scramjet

图8 超燃冲压发动机燃烧室最高温度Fig.8 The max temperature in combustion chamber of scramjet

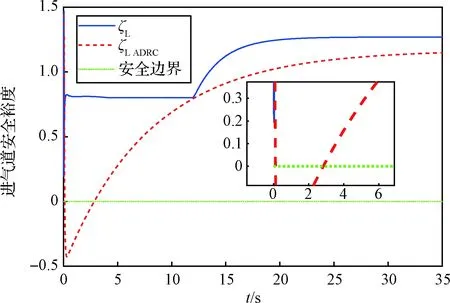
图9 超燃冲压发动机进气道安全裕度Fig.9 Inlet stability margin of scramjet

由图10、图11，当仅由提供推力会导致燃烧室最高温度靠近危险边界时(图8)，安全控制器及时降低了输出，而在性能子系统的控制下及时地作用以达到推力基本保持稳定输出(图10)；当速度与指令偏差较小，所需推力不大，且燃烧室最高温度远离危险边界时，认为超燃冲压发动机安全，安全子系统不对控制输入进行限制，性能子系统马上拉低的输出，使用燃烧效率更高的进行推力输出以期达到较小的燃料消耗。

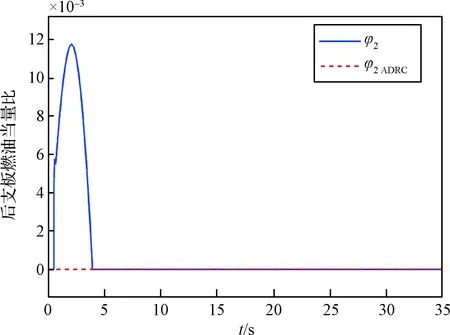
图11 后支板执行机构输出Fig.11 Output of the scramjets’rear actuator

该仿真中后支板未进入饱和，本文所使用的辅助系统在执行机构未发生饱和时并不启动，保证了较好的全局性能与稳定性；前期由于速度跟踪指令误差较大，前支板进入饱和，图10中 0.6的饱和上界是根据式(13)实时解算更新的，更新周期为0.1 s；执行机构进入饱和后，退饱和辅助系统及时起动，使前支板极快地退出饱和状态，降低了饱和非线性对控制系统的影响。

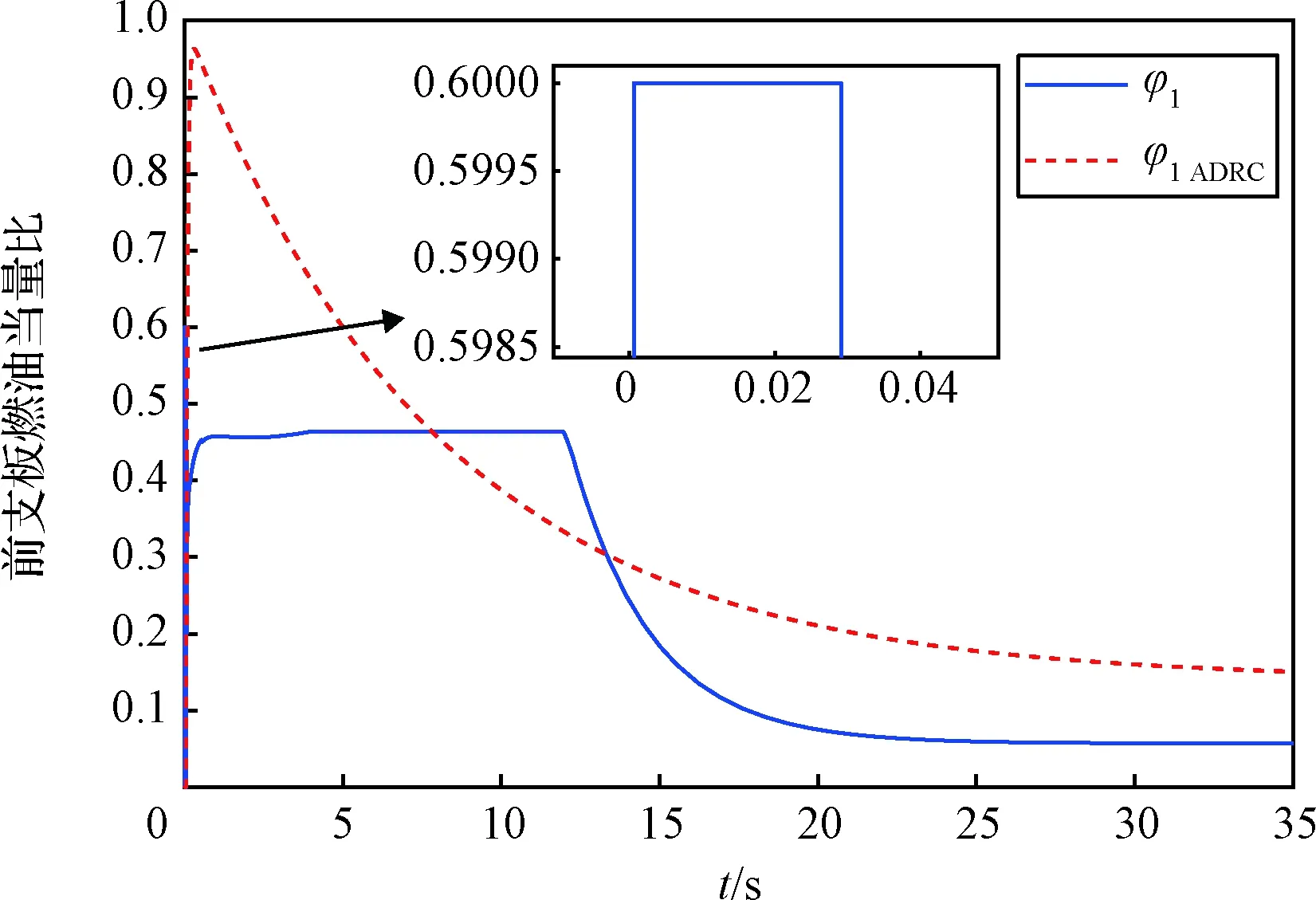
图10 前支板执行机构输出Fig.10 Output of the scramjets’front actuator

与之相比，ADRC系统未进行进气道稳定裕度的建模，因此没有单独针对的饱和约束，只有总的燃油当量比约束，即0<+<11。自抗扰控制下，执行机构均未进入饱和，但发动机工作状态已超出安全边界。

4 结 论

本文针对吸气式高超声速飞行器，基于飞-推一体化思想设计了保性能安全控制系统，相比传统的AHV控制方案，对发动机安全因素的考虑更真实全面；采用障碍Lyapunov函数从理论上保证了发动机的安全性，在发动机安全工作的前提下，该系统对飞行器攻角的约束可以放宽到10°，显著增强了高超声速飞行器的机动灵活性；同时辅助系统以及实时更新的饱和上界极大地降低了饱和非线性对控制系统的影响。仿真结果表明,本文所设计的控制器可以达到预想的控制性能。在安全子系统的控制下，超燃冲压发动机可以持续稳定的工作，同时不会给飞行器姿态控制子系统太大的约束压力；在性能子系统的控制下，超燃冲压发动机可以稳定地输出需求推力，以响应飞行器的速度跟踪需求，进而达到“保证安全的前提下不折损性能”的控制目的。