多弹最优协同诱导突防制导律

王宁宇,白瑜亮,魏金鹏,崔乃刚

(1.哈尔滨工业大学航天学院，哈尔滨 150001;2.沈阳飞机设计研究所，沈阳 110000)

0 引 言

随着防空反导武器技术的快速发展，传统单弹作战模式的突防能力受到极大挑战，导弹生存能力急剧下降。面对日益复杂的攻防对抗体系，将协同探测、协同规划、协同制导相结合的多弹协同突防的模式，能够更大限度地满足突防任务需求以及适应战场环境，有利于提升武器系统的突防能力，协同突防技术逐步成为航空航天领域的热点研究方向。近年来，以美国为代表的世界各军事大国在协同作战领域投入了大量精力，并取得了诸多代表性成果。美国于2018年成功开展了海军编队协同作战演习，并将无人机协同作战技术向智能化、自主化、集群化方向发展。俄罗斯和印度等国在武器协同突防方面的研究同样发展迅猛，突破了多项关键技术并制定了相关研究计划。

作为协同突防技术的关键组成部分，协同制导在突防概率、生存能力、协同规划方面有重大意义。特别是在末制导阶段，为实现多弹在能力需求较小的情况下完成协同突防任务，需要开展多弹协同最优协同突防制导律设计，以提升自身突防武器的生存概率。

众多国内外学者针对协同突防制导律的设计策略进行了深入研究，常见协同制导律主要采用主动反拦截、躲避机动和协同诱导等突防措施。尽管这些协同制导律策略都能够完成进攻弹的突防，但为增加进攻弹的突防概率，降低进攻过程的过载需求，提高进攻弹的生存概率，诱导协同突防制导律的设计更为有效。在多弹协同突防过程中，设计协同诱导制导律以完成突防任务是当前制导律研究的一个重要方向。设计诱导突防制导律最常见的方法是基于最优控制原理、微分对策算法和一致性理论，得到满足性能指标要求的制导指令解析解。Shima推导了三种基于最优控制原理的单边最优诱导制导律，验证了在防御弹和突防弹能力弱于拦截弹的情况下,防御弹也能够实现对突防弹的护卫任务。在文献[13]的基础上，Prokopov等推导并仿真验证了三种不同的双边协同线性二次型制导策略。Weiss等以拦截弹最大脱靶量和突防弹最小机动能力作为性能指标,采用微分对策原理推导了两种“突防-防御”协同诱导制导律。文献[16]以终端脱靶量为指标设计了相对博弈突防制导策略，使拦截器在不被防御器反拦截的情况下，实现对目标的突防打击任务。文献[17]针对“领弹-从弹”构型基于一致性理论并结合扩张状态观测器(ESO)理论，设计了分布式一体化协同诱导突防制导律。

目前协同诱导制导律在理论上已经获得了完整的解析解，并针对其解的性质和使用条件展开了详细讨论，但其假设进攻弹与拦截弹均为理想状态动力学特性，因此需开展基于任意阶动力学特性的诱导协同制导律设计，以真实反映其在工程实践中的可用性。

针对协同诱导制导律需要解决的关键问题，本文通过推导弹目相对运动方程，设计了一种最优协同诱导制导律，实现对拦截弹机动方向和运动趋势进行诱导，使得拦截弹的弹道呈现四维重叠(时间、位置)进而发生相互碰撞，最终实现协同诱导突防。不同于常规协同突防制导律，本文提出的方法不仅采用一致性原理对各拦截弹加速度进行精确估计，以提高协同制导律的诱导精度，而且可以通过诱导拦截弹相互碰撞提升进攻弹自身生存概率。最后，以2枚进攻弹对2枚拦截弹(2v2)对抗场景为例，仿真结果验证了方法的正确性，并针对不同拦截弹动态特性下的协同诱导制导律进行了有效性验证。

1 多弹协同诱导对抗数学模型

1.1 多弹协同非线性相对运动模型

针对多弹协同对抗作战场景进行建模。首先做如下假设：

1)记突防方飞行器为进攻弹(记为)，拦截方飞行器为拦截弹(记为)；

2)拦截方采用1v1拦截策略，即拦截弹用于拦截进攻弹；

3)由于在对抗末段开展相关协同诱导制导律的研究，假设所有进攻弹和拦截弹的速度大小不变。

图1给出了在纵平面内的多弹协同作战相对运动关系，其中，和分别表示第枚拦截弹和第枚进攻弹，和分别表示和的飞行速度，和分别表示和的弹道倾角，和分别表示和加速度，表示和之间的相对距离，表示速度方向与弹目连线的夹角，表示速度方向与弹目连线的夹角，表示从指向的视线角，表示与在垂直于初始视线方向的相对位置，+1表示和+1之间的相对距离，+1表示+1速度方向与和+1连线的夹角，+1表示速度方向与和+1连线的夹角，+1表示从指向+1的视线角，+1表示与+1在垂直于初始视线方向的相对位置。以上各量中=1,2,…,,为拦截弹或进攻弹总枚数。

图1 多弹协同相对运动关系图Fig.1 Multi-missile cooperative relative motion diagram

和之间非线性相对运动方程为：

(1)

(2)

和+1之间非线性相对运动方程为：

cos(-+1)

(3)

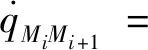
(4)

由图1中与之间的几何关系如下：

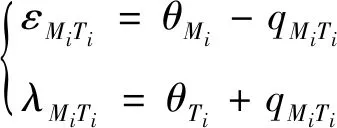
(5)

与+1之间的几何关系如下：

(6)

与的弹道倾角变化率如下：

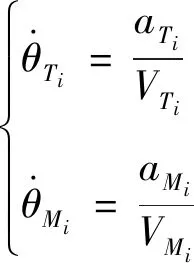
(7)

同时，为反映真实作战过程，将拦截弹和进攻弹的自动驾驶仪特性采用如下二阶微分方程表示：

(8)

(9)

采用传递函数的形式可将式(8)和式(9)分别表述为：

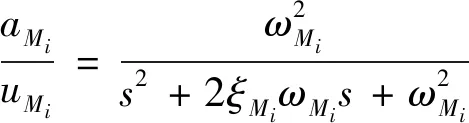
(10)

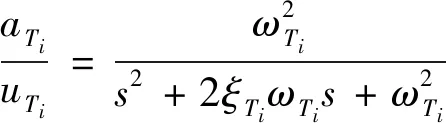
(11)

式中:为复参变量。

1.2 多弹协同诱导模型及线性化

为了设计协同诱导制导律，假设交战过程处于末制导阶段，进攻弹和拦截弹的速度大小基本保持不变，且始终位于碰撞三角形附近，因此可以初始视线为基准对原始的非线性模型进行线性化。为实现协同诱导碰撞，在多弹协同非线性相对运动模型基础上，引入拦截弹碰撞距离与碰撞角，构建多弹协同诱导模型，对协同诱导非线性相对运动方程进行线性化处理，可得到与之间的线性相对运动方程：

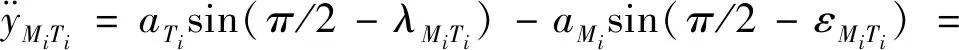
cos-cos

(12)

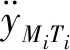
同理可得到用于描述与+1之间碰撞距离的线性相对运动方程如下：

+1)=-+1cos+1-cos+1

(13)

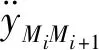
定义各拦截弹碰撞角为：

=+1++1=+-+1

(14)

为能够满足拦截弹在末端实现碰撞，需要保证拦截弹的速度方向尽快与各拦截弹连线方向重合，因此在碰撞末端满足：

+1(p)++1(p)=

(15)

式中：+1(p)和+1(p)分别表示和+1速度方向在终端碰撞时刻p时与和+1连线的夹角。

对式(14)进行求导：

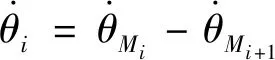
(16)

将式(7)代入到式(16)可得用于描述与+1之间碰撞角的线性相对运动方程如下：

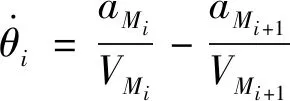
(17)

结合式(8)、(9)、(12)、(13)和(17)可得到线性化最优协同诱导突防制导律线性化状态向量如下：

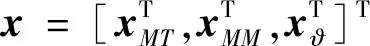
(18)

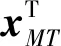
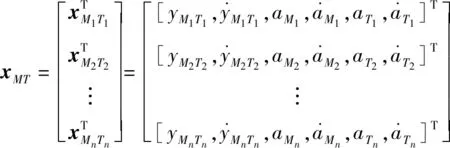
(19)

(20)

=[,,…,-1]

(21)

结合式(10)、(11)和(12)可得与之间状态方程如下：

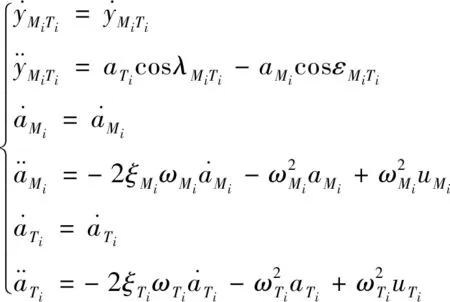
(22)

结合式(13)可得与+1之间关于碰撞距离的状态方程如下：

(23)

结合式(17)可得与+1之间关于碰撞角的状态方程如下：

(24)

将式(22)、(23)和(24)联立构成(9-3)维的协同诱导突防制导律的复杂状态方程。

2 最优协同诱导制导律设计

本节主要基于上一节中多弹协同作战相对运动关系，通过将拦截弹零控脱靶量和零控碰撞角引入相对运动关系中，得到协同诱导线性化相对运动方程，并利用状态转移矩阵进行降维处理;基于碰撞角约束设计快速收敛的扩展性能指标函数，通过约束拦截碰撞时间，采用最优控制原理推导多弹协同诱导解析制导律。之后通过推导2v2对抗场景下显式表达式，为典型对抗场景仿真验证提供解析制导指令。

2.1 协同诱导问题描述

结合式(22)对于和之间的状态方程如下：

()()

(25)

式中：

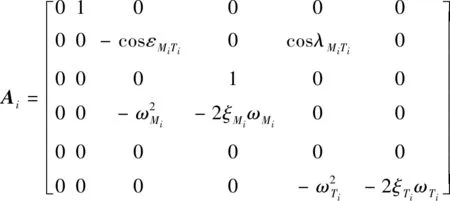
(26)

(27)

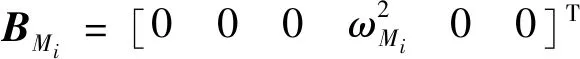
(28)

为求解协同诱导作战最优问题，通常需要采用状态转移矩阵进行降维处理，因此基于式(25)的和状态方程，得到零控脱靶量()的相关方程如下：

()=(f,)()

(29)

根据状态转移矩阵(f,)的性质：

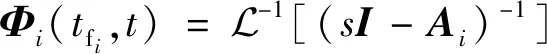
(30)

(31)

对式(29)求导并将式(25)代入可得：

(32)

在拦截弹飞行时间满足≥f时，飞行结束且其状态失去意义，因此采用单位阶跃函数1(f-)对其进行修正，单位阶跃函数定义如下：

(33)

令

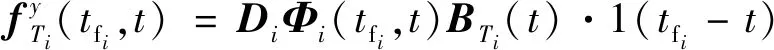
(34)

(35)

则式(32)可表示为

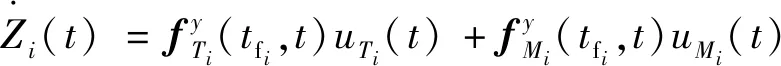
(36)

在进攻弹对拦截弹进行诱导碰撞过程中，定义p为与+1之间的碰撞时刻，记各拦截弹零控脱靶量+()，根据式(23)对+()进行求导可得：

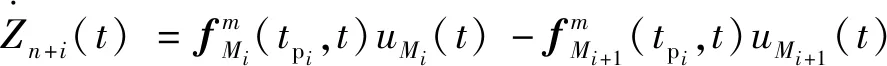
(37)

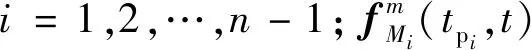
(38)

在进攻弹对拦截弹进行诱导过程中，拦截弹在碰撞时刻f得到的各拦截弹碰撞角即为零控碰撞角，记为2-1+()。根据式(24)对+()进行求导可得：

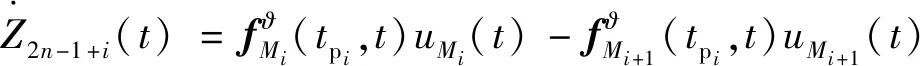
(39)

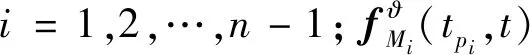
(40)

根据式(36)、(37)和(38)，定义多进攻弹对拦截弹的协同诱导状态变量如下：

()=[,…,,+1,…,2-1，2,…,3-2]

(41)

式中：前维变量为与之间的零控脱靶量;中间(-1)维变量为与+1之间的零控脱靶量;最后(-1)维变量为与+1之间的诱导零控碰撞角。

通过状态转移矩阵降维处理，诱导协同突防制导律状态变量由式(18)的(9-3)维降为式(41)的(3-2)维，极大降低了状态方程的复杂度，为接下来的求解提供了便利。

2.2 最优协同诱导制导律设计

将进攻弹对拦截弹的协同诱导问题的性能函数定义为：

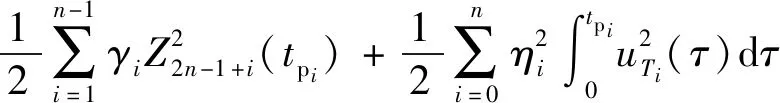
(42)

式中：,,,均为非负常数。

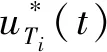
(43)

式中：是可用的加速度范围参数。

根据式(36)和(40)的状态方程以及式(40)的性能指标函数，协同诱导哈密顿函数可表示为：

(44)

根据式(44)，得到协同诱导伴随方程为：

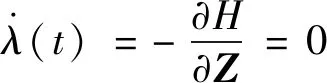
(45)

在最终拦截时刻f，伴随变量()的边界条件为：

(f)=(f),=1,…,

(46)

+(p)=+(p),=1,…,-1

(47)

2-1+(p)=2-1+(p),=1,…,-1

(48)

根据式(45)、(46)、(47)和(48)，伴随变量满足：

()=(p),=1,…,

(49)

+()=+(p),=1,…,-1

(50)

2-1+()=2-1+(p),=1,…,-1

(51)

可得进攻弹的最优控制策略满足

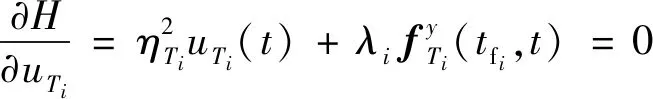
(52)

因此可得进攻弹的最优控制策略为：

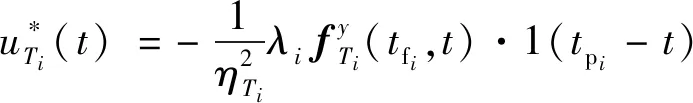
(53)

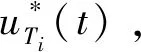
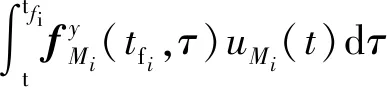
(54)

将式(49)、(50)、(51)代入到式(54)中可得：

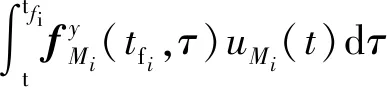
(55)

定义变量：

(56)

根据式(55)和(56)关于伴随变量的方程组可表示为：

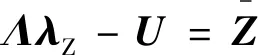
(57)

式(57)中的方程组共包含个方程，对应个未知的伴随变量，其中对于各拦截弹加速度信息的获取，通过采用文献[20]多飞行器一致性协同估计方法。首先，利用扩张状态观测器对各拦截弹加速度进行独立估计，设计一致性协调控制量，通过对局部估计信息交换得到各拦截弹一致性协同加速度估计值，因此式(57)可改写为：

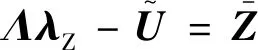
(58)

式中：

(59)

因此式(58)方程组可解。当拦截弹和进攻弹数量较少时，可采用解析解得到伴随变量表达式；当拦截弹和进攻弹数量较多时，可通过数值方法对伴随变量求解。将求解得到的伴随变量代入到式(53)中即得到进攻弹协同诱导突防制导律解析解。

为实现协同诱导突防任务，需保证拦截弹自相碰撞的时刻早于进攻弹被拦截弹拦截的时刻：

pf,f+1)

(60)

式中：f为对的拦截时间;p为与+1的碰撞时间。

在不进行协同诱导时，为保证式(60)成立，则应该尽可能减小p。因此构建如下碰撞三角形进行说明：

图2 初始碰撞三角形示意图Fig.2 Scheme of the initial collision triangle

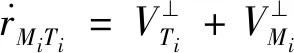
(61)

同理，两拦截弹碰撞过程相对速度如下：

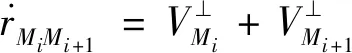
(62)

在每个时间步长处，针对于拦截弹和进攻弹进行剩余时间近似估计：

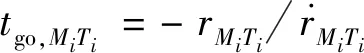
(63)

(64)

式中：go,表示与之间的剩余时间估计;go,+1表示与+1之间的碰撞剩余时间估计。

由图2可知，在拦截弹飞行过程中,当碰撞三角形保持较好时，拦截剩余时间估计误差较小；当由于对抗双方机动导致碰撞三角形变化较大时，上述剩余时间估算方法可能会导致较大误差，不能满足式(60)的约束条件。为解决这一问题，采用逼近go,+1的方式，其中定义如下：

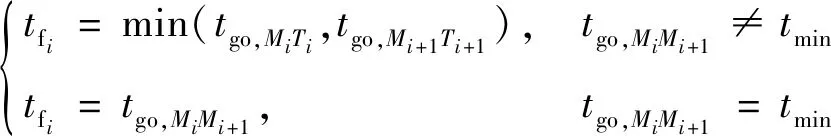
(65)

式中：=min(go,,go,+1+1,go,+1)。

式(65)虽然不能准确反映真实剩余时间估算结果，但它是一种可以避免违反式(60)的方法。

为方便仿真验证分析，针对典型2V2攻防对抗场景，基于式(53)求解显式解析解。

2.3 2v2攻防对抗下的解

基于2v2攻防对抗场景，通过对状态方程进行简化，整理得到关于伴随变量的方程为：

(66)

(67)

(68)

将式(68)代入到式(53)得到进攻弹1的协同诱导最优控制策略为：

(69)

进攻弹2的协同诱导最优控制策略为：

(70)

由于进攻弹均采用二阶自动驾驶仪特性，因此式(11)可表示为：

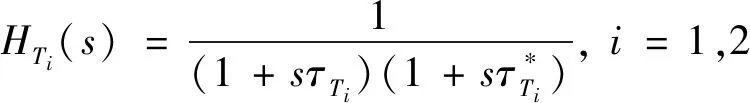
(71)

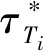
将式(26)代入式(30)中并进行求解可得：

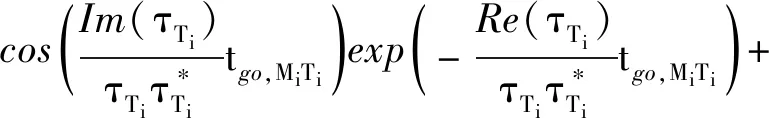
go,-2Re(),=1,2

(72)

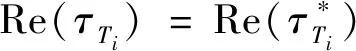
需要注意的是，本文提出的协同诱导制导律是基于进攻弹完整信息假设的，但在实际的交战场景中又是不现实的，比如和分别为进攻弹自动驾驶仪的阻尼比和固有频率，所以，为了实现这一制导律，往往需要在制导回路中增加滤波器，对进攻弹系统未知的状态和参数进行实时估计。

3 仿真分析

为验证本文设计的协同诱导制导律，假设拦截弹采用三种常规制导律完成对进攻弹的拦截任务，通过一致性协同扩张状态观测器对其加速度进行观测，基于观测值验证协同诱导制导律的有效性，并通过蒙特卡洛打靶验证不同拦截弹动态特性下协同诱导突防制导律的有效性。

3.1 拦截弹制导律设计

拦截弹采用如下线性制导律：

=+,=1,2,…,

(73)

其中，为拦截弹过载指令;为拦截弹对应进行拦截的进攻弹过载指令;为拦截弹状态向量，表达式见式(22)所示;为拦截弹状态制导系数矩阵，表达式见式(74)所示;为进攻弹过载系数。

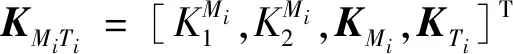
(74)

设拦截弹分别采用比例导引律(PN)、扩展比例导引律(APN)和最优导引律(OGL)作为拦截制导律，由文献[18]可知，拦截弹采用的各线性制导律系数如下：

(1)比例导引律(PN)系数

(75)

(2)扩展比例导引律(APN)系数

(76)

(3)最优导引律(OGL)系数

(77)

在式(75)～(77)中：go,为拦截弹飞行剩余时间,其表达式见式(63);和分别为拦截弹和进攻弹状态的维数;[]为与拦截弹和进攻弹状态维数相同的零矩阵;′为比例导引律系数;′为扩展比例导引律;′()为最优导引律系数，表达式如下：

=go,/

(78)

()=e-+-1

(79)

(80)

式中：为各拦截弹动力学阻尼常数。

3.2 协同诱导制导律算法验证

为验证本文一致性诱导协同制导律设计，采用2枚进攻弹对2枚拦截弹进行协同诱导突防作战过程，设计仿真初始条件如下：

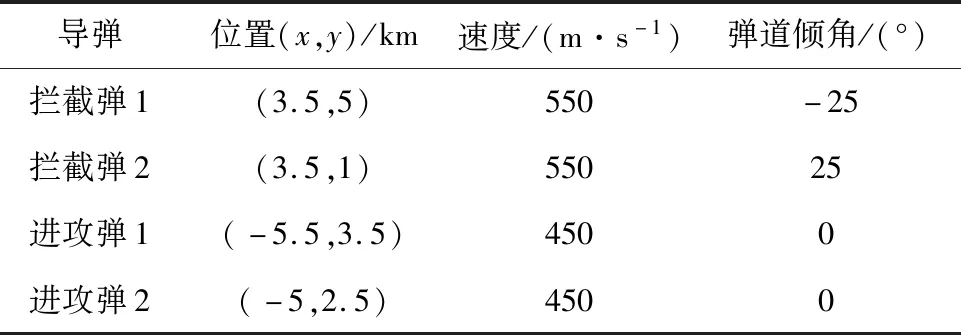
表1 拦截弹和进攻弹的初始运动状态Table 1 Initial motion states of interceptors and attackers

首先，各拦截弹采用比例导引律对进攻弹进行拦截，利用如式(73)和(74)线性制导律，然而各进攻弹事先无法获取拦截弹采用的制导律及制导参数，只能通过文献[20]一致性观测器对拦截弹加速度进行估计。

图3 进攻弹采用不同制导律情况下拦截弹飞行过程Fig.3 Flight curves of interceptors under different guidance laws for attackers

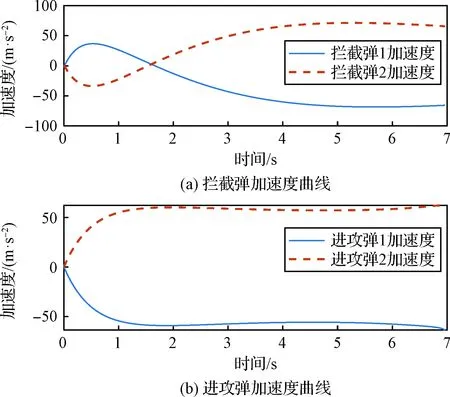
图4 拦截弹和进攻弹加速度曲线Fig.4 Acceleration curves of interceptors and attackers

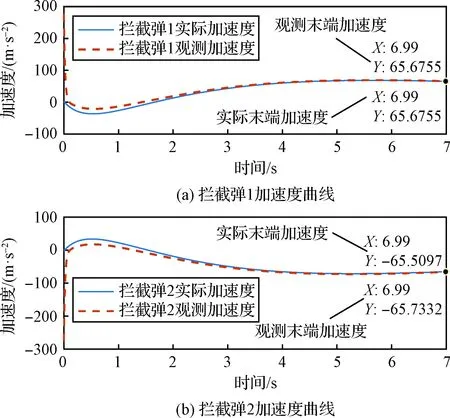
图5 对于拦截弹的一致性协同加速度估计Fig.5 Estimation of consistent coordinated acceleration for interceptors

图6 拦截弹采用不同制导律时的飞行曲线Fig.6 Flight curves of interceptors under different guidance laws

如图3(a)所示，在不采用协同突防制导律时，拦截弹1与进攻弹1的碰撞时刻为9.50 s，拦截弹2与进攻弹2的碰撞时刻为8.92 s，脱靶量分别为0.257 m和0.538 m，拦截弹均可以对进攻弹完成拦截任务。而采用协同诱导制导律时，如图3(b)所示，两拦截弹在6.99 s时便相互碰撞，且脱靶量为0.871 m，采用本文提出的最优协同制导律能够诱导拦截弹自相碰撞，进攻弹能够有效完成突防任务。

由图4可知，在采用协同诱导突防制导律的条件下拦截弹1和拦截弹2最大加速度分别为68.49 m/s和71.38 m/s，进攻弹1和进攻弹2最大加速度分别为66.75 m/s和62.16 m/s，在该组参数条件下，可以在进攻弹过载小于拦截弹过载的情况下实现诱导突防。

在图5中，拦截弹导引系数′=4.0时采用一致性加速度估计算法可对两拦截弹加速度进行精确估计，估计误差精度在10m/s量级左右，且逐渐收敛于真实值。当拦截弹采用APN制导律时，导引系数′=3.0；当拦截弹采用OGL制导律时，阻尼常数==0.2 s，采用两种不同制导律系数协同诱导突防最优制导律仿真结果如下。

如图6所示，在拦截弹采用不同制导律对进攻弹进行拦截过程中，通过对本文协同诱导突防制导律各参数进行调整，进攻弹均能实现对拦截弹诱导碰撞过程，从而验证了本文提出制导律在真实作战环境下的有效性和可行性。

考虑在作战过程中拦截弹实际动态特性与理想动态特性存在误差，因此设置拦截弹动态特性参数为服从均匀分布的干扰因素如表2所示，进行128次蒙特卡洛打靶仿真，结果见图7～图8。

表2 干扰因素列表Table 2 List of disturbances

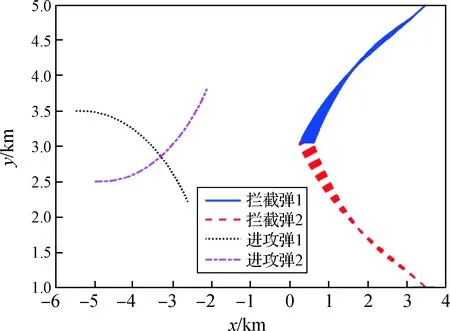
图7 采用协同诱导制导律情况下拦截弹飞行过程Fig.7 Flight curves of interceptors under cooperative guidance law

图8 拦截弹和进攻弹加速度曲线Fig.8 Acceleration curves of interceptors and attackers

图7展示了采用协同诱导突防制导律的情况下,拦截弹终端脱靶量最大值为1.7121 m，最小值为 0.7374 m，进攻弹均能诱导拦截弹自相碰撞。图8展示了打靶仿真各拦截弹和进攻弹的加速度值，其中拦截弹1和拦截弹2最大加速度分别为75.0802 m/s和80.9384 m/s，进攻弹1和进攻弹2最大加速度分别为73.9309 m/s和72.0264 m/s。根据仿真结果可见，在考虑拦截弹不同动力学特性参数的情况下，本文提出的协同诱导突防制导律仍然能够实现对拦截弹诱导碰撞的过程，并同时满足进攻弹能力要求。

5 结 论

本文针对多弹协同突防问题提出了一种基于诱导碰撞策略的多弹最优协同诱导突防制导律。考虑拦截弹和进攻弹均为二阶驾驶仪动力学特性，通过引入拦截弹碰撞距离和拦截弹碰撞角构建了多弹协同对抗非线性模型。利用状态转移矩阵实现高维非线性模型进行降维，通过引入碰撞角约束设计了具有快速收敛的扩展性能指标函数。采用一致性估计方法获得拦截弹加速度信息，并基于碰撞时间匹配策略推导了多弹最优协同诱导解析制导律一般形式，最后给出2V2典型场景下的制导律显式解析形式。通过典型场景仿真验证了最优协同诱导突防制导律的正确性，并对不同拦截弹动态特性进行仿真分析，验证了本文提出的诱导突防制导律的鲁棒性。