飞行器制导控制一体化编队控制器设计

陈昶荣，许 鑫

(北京机电工程研究所，北京 100074)

0 引 言

飞行器协同编队飞行是指将多个具有自主功能的飞行器按照一定相对位置进行三维空间分布，使其在飞行过程中构建并保持设计的队形。编队飞行中的个体通过合作协调能够提高系统整体的性能，是提升精确制导武器的电子对抗能力、协同突防能力、大范围分布目标的搜索能力和识别能力，降低作战消耗，提高效费比等综合作战效能的必由途径，适用于日益复杂的作战需求。

目前，国内外关于飞行器协同编队控制策略进行了比较深入的研究，提出了集中式和分布式两种编队结构，集中式是指通过一个集中协调单元获取充分的全局信息后，计算并逐一输出各个飞行器需要的制导指令，而分布式则是指每个飞行器只依靠自身获取和邻近个体传递的局部信息，导引自身完成队形。集中式编队方法原理简单，在编队个体存在故障的情况下，对其他个体编队飞行影响甚微，故在编队控制中应用最为广泛。

由于人为或自然因素，飞行器飞行过程中会受到多方面的干扰，国内外学者针对外界干扰问题进行了研究。文献[4]采用自抗扰控制技术对控制器进行设计，并通过粒子群算法对控制器参数寻优，实现了非线性耦合的编队飞行系统的合理控制；文献[5]针对存在不确定非线性动态和外部时变干扰的多无人机系统的编队问题，采用扩张状态观测器估计无人机系统的不确定性，提出抗扰动编队控制律；文献[6]将非奇异终端滑模控制和干扰观测器控制方法相结合，为自主体系统提出了一种主动抗干扰协同控制方案；文献[7]对无人系统的动态反馈进行线性化处理，将自抗扰控制和预测控制相结合，对无法建模的扰动进行估计并补偿，使编队控制更精确。

但是对于任何飞行器，由于物理条件的限制，执行机构的输入控制量受到约束，通常表现为饱和的非线性，使控制效果表现为病态。针对控制量饱和问题，文献[8]基于单领导者编队控制思想，根据跟随者位置和预设位置的偏差建立状态方程，并考虑控制量受限的情况，设计自适应滑模编队控制器，对预先规划航路点进行快速精确跟踪；文献[9]引入了饱和函数，采用饱和控制理论对控制系统进行分析，提出了一种输入饱和约束下的控制算法；文献[10]考虑非对称饱和控制器，将饱和控制输入转化为扰动，采用有限时间观测器对该扰动进行观测，得到饱和输入条件下的编队控制律；文献[11]设计了辅助系统，飞行器可根据执行机构是否处于饱和状态，选取一套合适的参数，解决控制饱和问题。

近年来随着人们对仿鸟类队形编队方式的研究，认识到当飞行器在适当安全距离内，通过紧密编队的方法可以减小整体飞行阻力，节约燃油，提高航程。文献[12]针对无人机密集编队飞行控制存在强耦合、强非线性以及强鲁棒性的要求，提出了运动模型解耦和单通道设计方法，同时采用改进反演方法设计了控制器，该方法降低了设计难度和保守性；文献[13]通过分析雁群长途迁徙过程中的编队飞行机制，讨论了编队飞行与雁群行为机制间的仿生映射机理，设计了一种仿雁群行为机制的多无人机紧密编队构型及控制方法。文献[14]受到大雁飞行时头雁产生的上洗气流能有效减小雁群飞行所需体力消耗的启发，提出了一种基于莱维飞行鸽群优化编队控制器参数的整定方法，设计了无人机编队远距离飞行时的比例-积分-微分仿雁群编队控制器。

但是，以上文献在设计编队飞行控制器时未充分考虑飞行器制导回路与控制回路之间的耦合作用，假设飞行器为解耦的自动驾驶仪，飞行器运动模型采用一阶或二阶闭环稳定系统，过于简化对象；并且在飞行器高速飞行的情况下，制导与控制系统之间的耦合作用更加明显，要求控制系统的响应速度更快。所以在六自由度高速飞行情况下，以上文献所提出的控制律存在编队精度下降甚至编队失败的问题。

而制导控制一体化(Integrated guidance and control,IGC)方法综合考虑了制导回路与控制回路之间的相互作用，将其视为一个整体，同时具备导引和姿态控制两项功能，实现制导与控制的无缝结合，其结构如图1所示。另外，该方法仅考虑一个闭环系统，简化了控制系统的设计过程，无需因为飞行环境的变化而反复设计控制系统。

图1 IGC设计方法结构框图Fig.1 The structure diagram of IGC design method

本文采用主从式编队方法，以侧滑转弯(Skid to turn,STT)飞行器为研究对象，充分考虑六自由度下飞行器的真实情况，采用IGC方法，设计飞行器编队飞行控制系统。首先，在惯性坐标系中定义相对运动坐标系，建立相对运动模型，结合飞行器动力学模型，引入建模误差，减小了系统的耦合程度，简化了模型的数学表达形式，得到全状态IGC模型；然后借鉴分块控制思想，将全状态IGC模型划分为编队控制、过载控制、姿态控制三个子系统，采用反演方法，结合滑模变结构控制与径向基函数(Radial basis function,RBF)神经网络自适应理论设计了IGC编队控制器，并证明了控制系统稳定性；最后在高速飞行情况下进行了六自由度数值仿真，分析了IGC设计方法与分离设计方法的控制性能，对比说明了IGC设计方法的优越性。

1 制导控制一体化数学模型建立

1.1 飞行器相对运动模型

如图2所示，建立相对运动坐标系-，坐标系原点位于领导者质心处，坐标轴方向与惯性坐标系-方向一致，即轴水平朝右，轴沿垂线向上，轴与其他两轴垂直并构成右手坐标系。

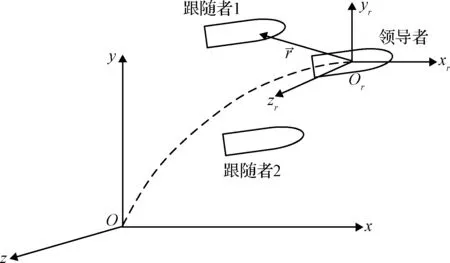
图2 惯性坐标系与相对运动坐标系Fig.2 Inertial coordinate system and relative motion coordinate system

在惯性坐标系中，领导者与跟随者的运动学方程分别为

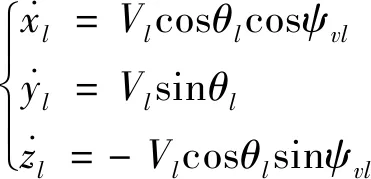
(1)

(2)

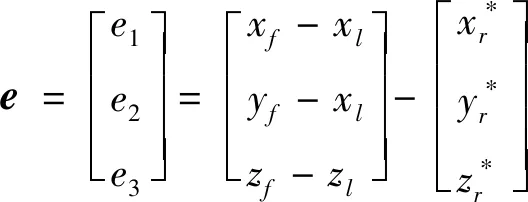
(3)

求导可得

(4)

由式(2)可得

(5)

根据运动状态与过载的关系有

(6)

其中，为重力加速度；,,为过载指令。结合式(5)～(6)可得

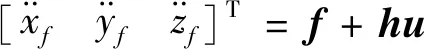
(7)

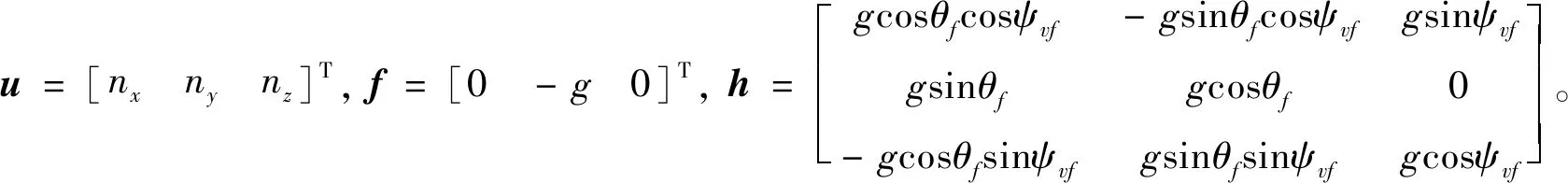
(8)

结合式(4)、(7)、(8)得到

(9)

1.2 飞行器动力学模型

根据文献[15]的建模过程，可得跟随者攻角为

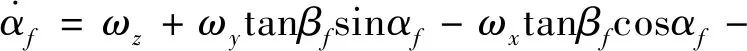
(10)

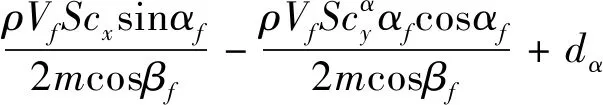
(11)

同理，可得跟随者侧滑角满足

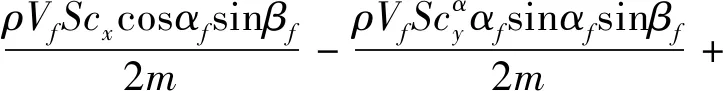
(12)

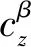
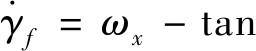
(13)

认为速度倾斜角与滚转角近似相等，即≈，记建模误差为，有

(14)

联立式(11)、(12)、(14)，并结合飞行器姿态动力学方程，可得跟随者动力学方程的标准形式如下

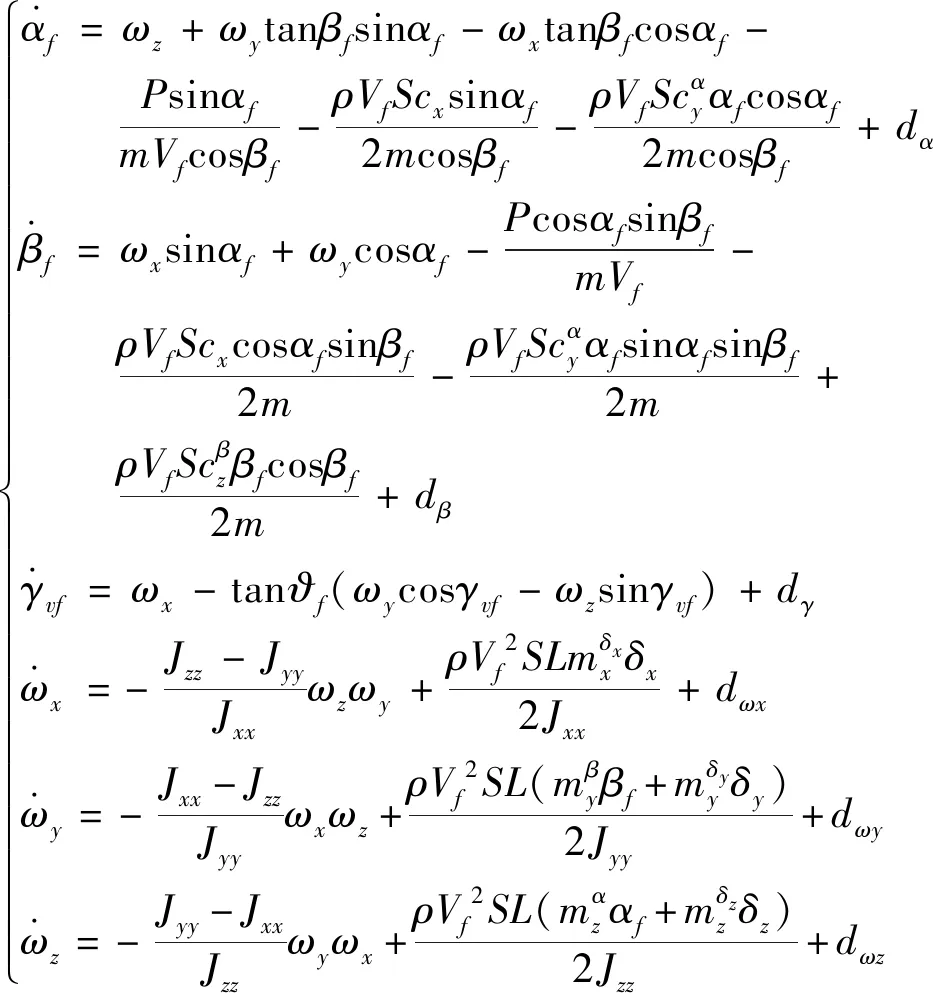
(15)

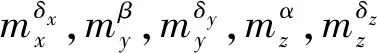
1.3 飞行器编队全状态IGC模型

假设气动力主要由攻角、侧滑角提供，舵偏角的影响较小，做以下近似

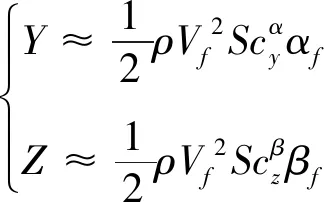
(16)

为了简化模型，近似认为纵向过载只与升力有关，侧向过载只与侧向力有关，将以上近似处理带来的建模误差视为扰动量。于是得到

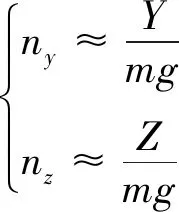
(17)

联立式(9)、(16)、(17)，可得

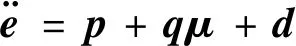
(18)

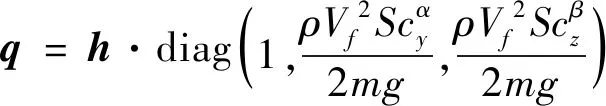
(19)

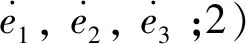
(20)

式中各个矩阵定义如下

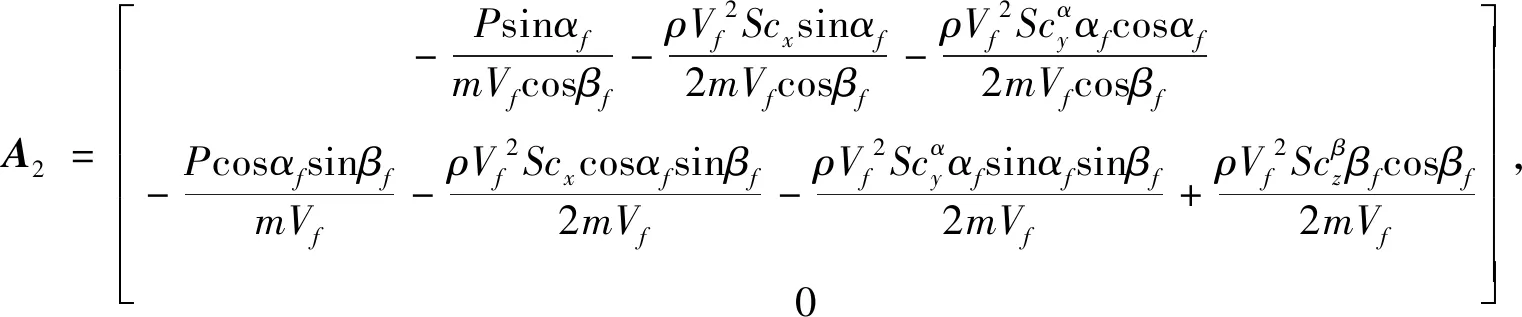
2 控制器设计

为了与分离设计方法(见文献[16])进行对比，本文中轴向过载控制器与文献[16]中控制器保持一致，针对偏航、俯仰、滚转三通道的IGC控制器进行设计。

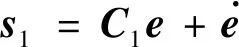
(21)

(22)

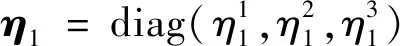
(23)

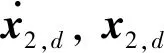
(24)

式中:为滤波器时间常数。

=-2,

(25)

构造虚拟控制量如下

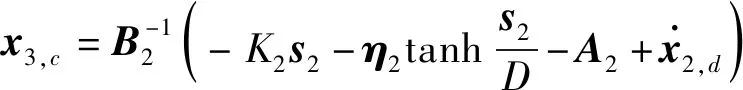
(26)

(27)

式中:为滤波器时间常数。

=-3,

(28)

设计控制律为

(29)

3 稳定性分析

以上设计的控制器产生的误差主要包括3个部分，即滤波器误差、神经网络权值误差和滑模面误差。

1)滤波器误差

=+1,-+1,=1,2

(30)

定义

(31)

其导数为

(32)

2)神经网络权值误差

由于神经网络的万能逼近特性，可设扰动量满足

(33)

神经网络的最优权值定义为

(34)

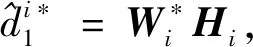
(35)

则神经网络自适应估计误差为

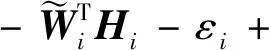
(36)

(37)

求导得

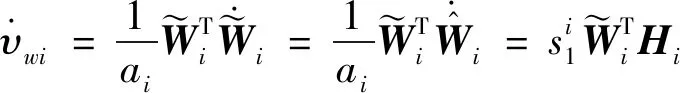
(38)

3)滑模面误差

由式(22)、(26)、(29)，可得

(39)

设

(40)

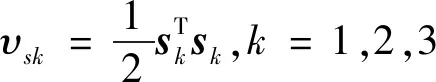
(41)

其导数为

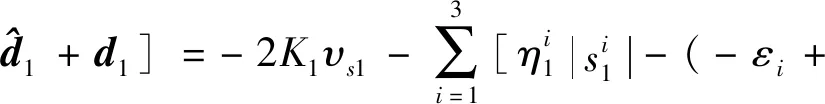
(42)

(43)

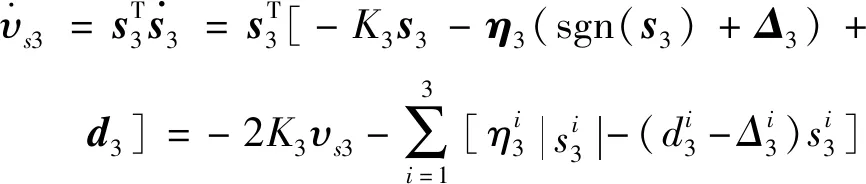
(44)

取Lyapunov候选函数为

(45)

其导数

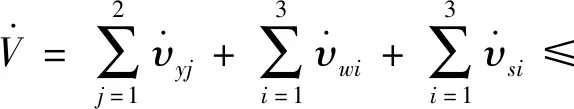
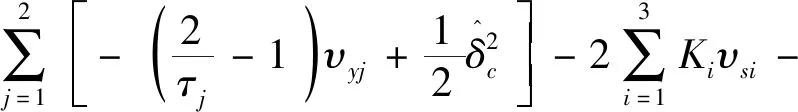
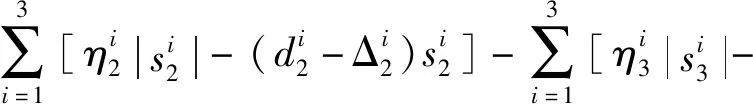
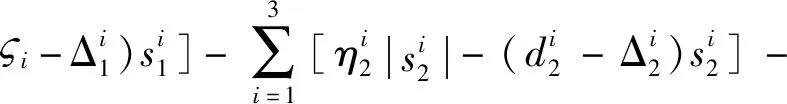
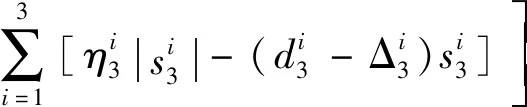
(46)

当满足

(47)

并取

(48)

则有

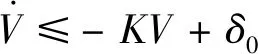
(49)

根据比较原理，可知Lyapunov候选函数满足

(50)

故系统所有状态和控制量稳定。

4 仿真分析

4.1 仿真条件

1)领导者状态

取领导者在惯性坐标系下初始位置为 0=0 m, 0=20000 m, 0=0 m；运动状态变化规律为

=1000 m/s,=0 rad，

=003sin(01+07728)rad。

2)跟随者初始位置

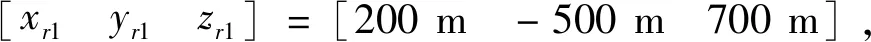
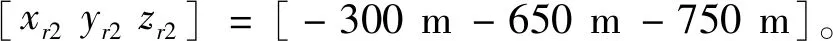
3)跟随者期望位置

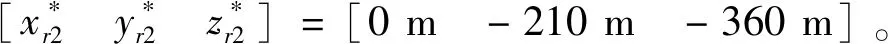
4)跟随者初始状态

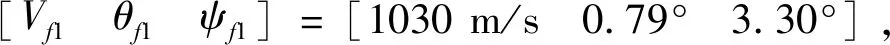
5)IGC控制器参数

(1)第一个子系统

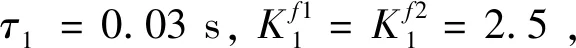
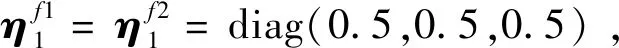
(2)第二个子系统

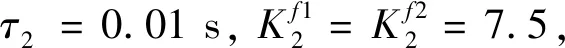
(3)第三个子系统

6)神经网络参数

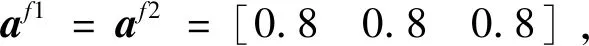
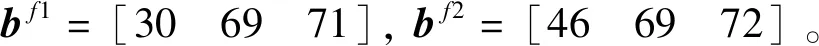
7)外界干扰

考虑表1所示的突风干扰作为主要干扰。

表1 跟随者所加干扰Table 1 Disturbance imposed on followers

8)分离设计方法

分离设计方法详见文献[16]，相关的运动参数、制导控制参数与本文设置一致。为了体现分离设计方法中，控制回路响应时间对编队控制性能的影响，将跟随者1与跟随者2控制回路时间响应时间设置不一致。其中跟随者1的控制回路响应时间稍短，纵向通道约2.0 s，侧向通道约1.6 s，代表控制回路响应稍快的情况；跟随者2的控制回路响应时间稍长，纵向通道约2.4 s，侧向通道约2.1 s，代表控制回路响应稍慢的情况。

4.2 结果分析

IGC方法的数值仿真结果如图3～7所示，文献[16]中分离设计方法的数值仿真结果如图8～10所示。从中可以得到以下结论：

1)由图3～4可知，在高速情况下，IGC编队控制器能够完成飞行器编队队形的构建与保持，在外界干扰和建模误差的作用下，能保持高控制精度。说明控制器对匹配不确定性和非匹配不确定性均具有良好的鲁棒性。

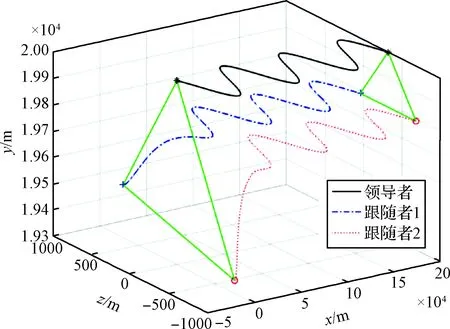
图3 编队飞行轨迹Fig.3 Formation flight path

2)由图5～7可知，突风干扰对偏航通道的影响较大，而对俯仰通道的影响较小。这是由于对俯仰通道起作用的是纵风，而在飞行器编队过程中，飞行器的航迹倾角很小，所以纵风的影响甚微；横风主要影响的是偏航通道，产生附加侧滑角，对偏航通道产生扰动。

3)由图8～10可知，高速情况下，采用分离设计方法，虽然跟随者1的编队误差收敛，但在初始时刻其舵偏角饱和，并且存在严重的抖振问题，原因是在编队初始时刻，编队误差大，跟随者1控制回路响应速度较快，基于误差控制的控制回路受到冲击大，在初始时刻产生较大的舵偏角，抖动程度大。

4)由图8～10可知，高速情况下，采用分离设计方法，跟随者2在纵向编队控制发散，进而影响到侧向和横向的编队控制精度，飞行器编队失败。这是由于跟随者2控制回路的响应时间较长，在高速条件下，控制回路产生的过载响应无法快速跟踪制导回路提供的过载指令，滞后时间长，导致编队控制系统闭环发散，编队失败。而跟随者2的侧向通道在突风干扰结束时刻(20 s)存在抖振现象，与跟随者1同理，说明对抵抗干扰而言,控制回路响应较快；而突风干扰结束之后，侧向通道以长周期(周期约4.5 s)运动缓慢收敛，该过程持续时间约40 s，说明对干扰结束后收敛速度而言,控制回路响应较慢。

5)由4.1可知，跟随者1和跟随者2的响应时间相差很小，仅约0.4～0.5 s，在很小的差值下，响应速度较快的跟随者1舵偏角抖振程度大，而响应速度较慢的跟随者2编队发散，并且跟随者2的侧向通道控制性能难以同时满足抵抗干扰平稳性和干扰结束后收敛快速性的要求。故在高速情况下，分离设计方法中控制参数设计范围窄，控制性能较差，并且外界环境容易导致控制系统由收敛状态变为发散状态。

6)由图5～7可知，对比于分离设计方法，采用IGC设计方法,飞行器舵偏角变化平缓，抖动程度小，并且在突风干扰结束后收敛速度快(收敛时间约2 s)，编队控制性能良好，这是由于IGC方法将编队控制系统考虑为一个闭环系统，无制导回路与控制回路之间的耦合作用。同时，IGC方法将外界环境参数考虑在控制器设计过程中，无需因为飞行环境的变化而反复设计控制系统，简化了控制系统的设计过程，提高了控制参数对环境的适应性。说明在高速情况下，IGC设计方法控制性能和设计难易程度相比于分离设计方法优势明显。

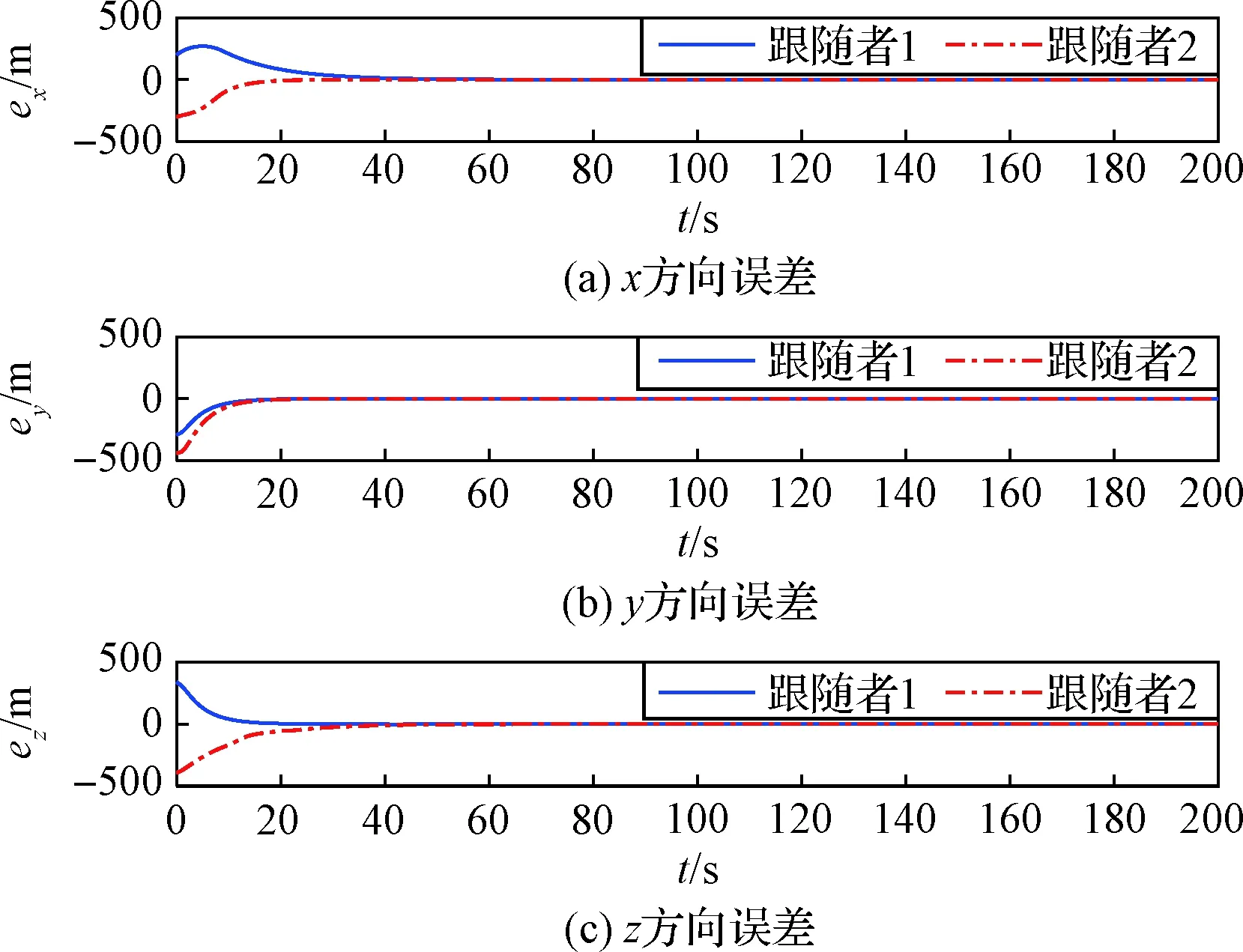
图4 三个方向控制误差Fig.4 Control error of three directions

图5 跟随者副翼舵偏角Fig.5 Aileron deflection angle of followers

图6 跟随者方向舵偏角Fig.6 Rudder deflection angle of followers

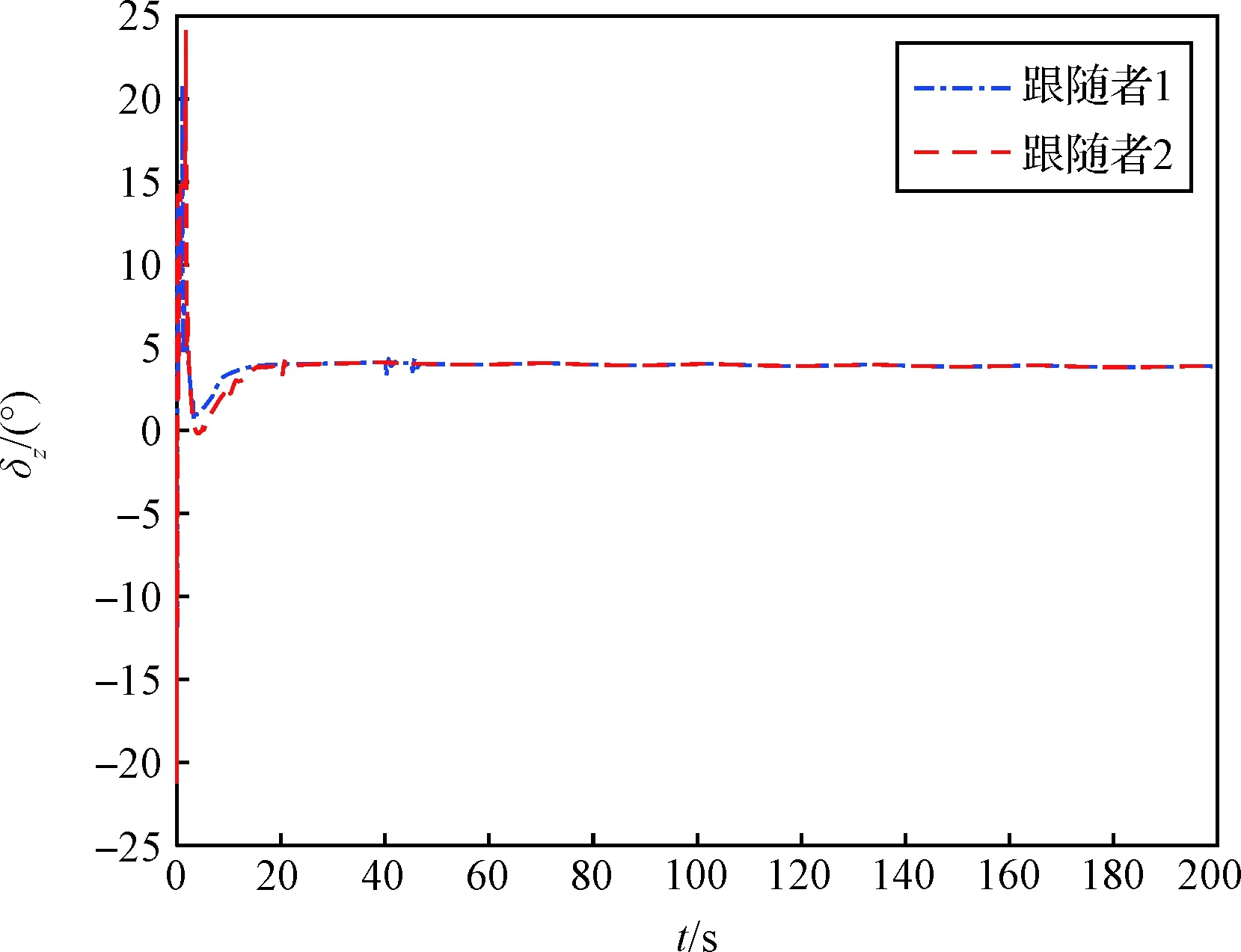
图7 跟随者升降舵偏角Fig.7 Elevator deflection angle of followers

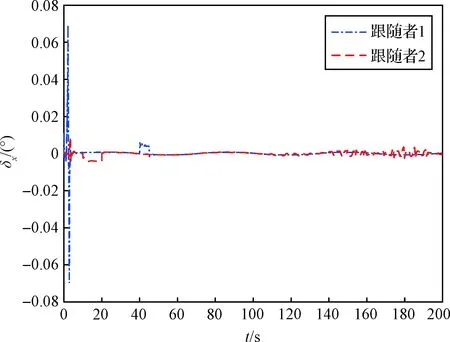
图8 文献[16]中副翼舵偏角Fig.8 Aileron deflection angle in reference[16]

图9 文献[16]中方向舵偏角Fig.9 Rudder deflection angle in reference[16]

图10 文献[16]中升降舵偏角Fig.10 Elevator deflection angle in reference[16]

5 结 论

本文针对STT飞行器编队飞行控制问题，建立了全状态IGC编队模型，采用IGC方法设计控制器，并进行了六自由度数值仿真。主要创新点包括：

1)建模过程中，利用控制系统对建模误差的鲁棒性做了如下近似：认为速度坐标系下的气动参数与体坐标系下的气动参数近似相等；认为航迹坐标系与体坐标系中的过载近似相等；忽略气动力中舵偏角带来的分量。合理地引入建模误差，减小了系统的耦合程度，简化了模型的数学表达形式，为控制器的设计提供了便利。

2)在高速飞行情况下，对比了IGC方法与分离设计方法的控制性能。基于分离设计方法的控制器难以满足快速性控制需求，响应速度稍快导致控制量饱和且抖动大，响应速度稍慢导致控制系统发散，并且对飞行环境的适应性差。而基于IGC设计方法的控制器对匹配不确定性和非匹配不确定性均具有一定的鲁棒性，飞行器舵偏角变化平缓，抖动程度小，干扰结束之后收敛速度快，编队控制性能良好，所以IGC方法更加有优势。