基于上升轨迹可达范围的目标拦截发射窗口计算

贾飞达，韩宏伟，温昶煊

(1.北京理工大学宇航学院，北京 100081；2.深空探测自主导航与控制工信部重点实验室，北京 100081)

0 引 言

近地空间是人类进行通讯、监测、导航等活动的重要位置，针对低轨目标的精确拦截是保证近地空间安全的有效手段。近地空间中时刻存在着大量飞行器，当发现已废弃的或对自身安全存在威胁的空间目标时，需要及时拦截、清除。快速可靠地确定发射窗口是实现低轨目标拦截的重要前提。

针对一般任务的发射窗口设计问题，目前已有大量的研究。李海阳等、李革非等研究了两航天器交会对接问题中的可交会发射窗口。首先分别考虑轨道光照角和太阳抑制角约束设计目标器和追踪器的发射窗口，之后根据轨道共面约束和交会对接发射时间间隔要求确定交会对接窗口。贺邵飞等基于固定的火箭飞行地心角和飞行时间，根据发射点和目标点位置关系，利用球面几何原理，提出了快速响应太阳同步轨道及发射窗口的解析计算方法。方虎涛对弹道导弹的发射窗口进行研究，考虑月球夹角、太阳光照射等条件，在二体问题中设计转移轨道，在此基础上考虑摄动力保证发射窗口精度。周文勇等通过搜索与解算上面级飞行姿态来满足长时间滑行期间的热控、地面测控等多种约束条件，将发射窗口计算问题转换为飞行姿态设计问题，提出了上面级发射窗口计算的方法与流程。Petropoulosr等提出了一种较有效的基于形状的搜索算法，该算法通过指数函数来描述探测器的飞行轨迹，从而进行发射时机搜索。上述对发射窗口的研究大多是在任务准备时间充足，充分考虑光照、共面等约束条件下进行设计，未考虑特定目标的拦截约束，在目标威胁较大、需要尽快拦截清除时难以应用。

针对导弹目标拦截的窗口设计问题，Yin等针对飞航式的反舰导弹目标，深入研究了海基防空导弹发射时间窗口计算问题，其针对的拦截目标一般为近程低空导弹，对应的发射窗口较窄。荆武兴等提出了一种基于迭代最小二乘的飞行方案及发射时间窗口的快速搜索设计算法，需要对初始状态进行猜测，且得到的窗口为离散点。吴启星等对弹道导弹中段拦截的拦截窗口进行研究，对采用最小能量弹道飞行的拦截弹道导弹能够拦截目标的最早和最晚拦截时刻进行求解，分析了射程、飞行时长和拦截时刻的关系，其研究中的拦截弹同样为在轨拦截器。梁子璇等提出一种针对高超声速目标拦截的末段交战窗口快速生成方法，但是其研究针对的是末端交战位置范围窗口，与本文定义有所差异。Hu等基于拦截弹和目标弹道导弹的弹道平面共面的假设，通过简单判定拦截弹的拦截高界、拦截低界、最大拦截斜距、最小拦截斜距这四个参数与目标弹和发射点的实时高度和斜距之间的大小关系，确定对目标弹的拦截最早时间和最晚时间，其应用的平面模型只能给出共面情况下的拦截时间窗口。

针对航天器目标拦截的窗口设计问题，Duan基于航天器二维可达域，首先考虑等待时长约束计算目标轨道上的可达相位范围，然后基于拦截器燃料约束，进一步判定位于拦截器可达域内的目标轨道可达相位范围，最后根据总任务时长的约束得到最终的交会窗口。然而，该方法仅适用于天基拦截问题，无法求解面向航天器目标的地基发射拦截问题。利用可达范围和目标轨道几何关系的发射窗口计算方法可以有效解决此类问题。

近年来，可达范围的概念被广泛地用于航天器轨道机动、复杂任务规划等领域。由于可达范围给定了所有的可行解集，且可通过离线计算实现预先存储，在实现自主、快速任务规划时具有显著优势。1960年，Beckner首先对地面发射的弹道导弹可达范围进行研究，提出可达范围的概念。21世纪以来，有学者考虑燃料约束对时间自由的航天器单脉冲可达范围进行分析，分别给出了二维轨道面和三维空间中航天器的可达范围计算方法。Qiao等对采用行星借力实现小天体探测的可达目标范围进行研究，有效地降低了发射能量和总速度增量。石昊等基于变参数的自适应同伦算法，提出一种适用于椭圆参考轨道的计算方法，计算航天器轨道初值不确定造成的可达区域。但是现有的可达范围计算方法针对的目标绝大多数都是在轨航天器，且一般为单脉冲可达范围，对于火箭在燃料约束下的空间可达范围研究较少。

因此，针对面向低轨目标拦截的发射窗口计算问题，提出一种基于上升轨迹可达范围的求解方法。该方法的具体步骤如下：首先，以上升时长为性能指标，得到上升到特定高度的最长和最短时间；然后，将性能指标切换为航程，可以得到不同上升时长分别对应的拦截范围；其次，根据目标拦截器的星下点与最大可拦截范围的关系对发射窗口进行初筛，得到若干准发射窗口，可以大大减小精确窗口规划的计算量；最后，通过精确判定准发射窗口中目标星下点与每一上升时长可达范围子环的位置关系，能够快速得到准确的发射窗口。

本文提出的基于可达范围的面向低轨目标拦截的发射窗口计算方法，根据目标的高度信息即可得到拦截器精确可达范围，然后根据目标的星下点信息可得多段精确发射窗口，解决了考虑三维运动的地基发射拦截器对在轨目标的拦截问题。仿真结果表明了该方法的有效性。

1 上升轨迹动力学模型

从地表上升的拦截任务要分别经历气动力耦合的大气上升段和弱摄动力下的空间轨道机动段，属于跨域大范围复杂约束机动弹道规划问题。

针对整个阶段的弹道规划问题，考虑发动机推力和地球引力作用，在球坐标系下建立弹道规划的动力学模型。拦截器上升段动力学方程为

(1)

式中：=[,,,,,,]分别为径向距离、经度、纬度、速度、飞行路径角、航向角和质量;控制量=[,,]分别为攻角、倾侧角和推力;为地球引力常数;为发动机喷气速度;为拦截器所受阻力，计算公式为

(2)

式中：为大气密度;为拦截器参考面积;为拦截器本身的阻力系数。

地球大气密度在地面时最大，随高度升高而逐渐减小，大气密度一般在距离地面130 km高度以上时可以被忽略。在此，大气近似应用指数模型，具体形式为

=e-

(3)

式中：=1225，为地球表面大气密度；=17100为大气密度指数参数；为距离地面高度。

2 上升轨迹可达范围计算方法

上升轨迹可达范围为拦截器在给定控制和飞行时长约束下能够到达的空间范围，记为。设参考坐标系为地心固连系，火箭垂直上升到达大气层边界后，一级助推继续推进至其燃料用尽后，二级助推继续推进至燃料全部消耗完毕，发动机关闭，拦截器滑行至目标附近进行追赶拦截等操作。

的求解包含两类：(1)固定飞行时长的上升轨迹可达范围;(2)固定高度的上升轨迹可达范围。针对第1类，记拦截器在固定飞行时长的可达范围求解问题(,)，其中是初始时刻，为末端时刻。针对第(2)类，记给定高度拦截器在一定飞行时长范围内的可达范围求解问题(,)。要求解区域，需确定其边界∂。

求解上升轨迹可达范围的边界可转化为最优控制问题，即特定性能指标函数下的最优飞行弹道，可以用经典的寻优算法进行求解。由于伪谱法是目前应用最广且算法鲁棒性最好的一类直接方法，本文采用文献[18]中的自适应伪谱法计算拦截器的上升轨迹。

记=-为拦截器从起飞至实现目标拦截的飞行时长，两类问题中涉及的性能指标包括：以飞行时长为性能指标=；以末端高度为性能指标=；以拦截器飞行航程为性能指标=。

2.1 固定飞行时长的上升轨迹可达范围

针对问题(,)，其飞行时长为定值。固定飞行时长的上升轨迹可达范围如图1所示，其中和分别为拦截器能够到达的最小和最大高度。

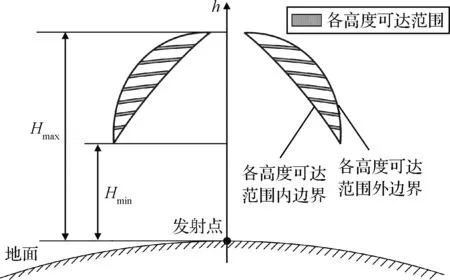
图1 特定飞行时长可达范围剖面Fig.1 Profile of the reachable domain with a fixed flight duration

第一步即要确定拦截器能够到达的高度范围，此时性能指标选取为末端高度，记为

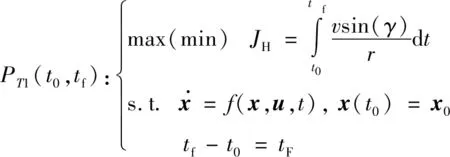
(4)

其中，“max”对应性能指标最大，“min”对应性能指标最小，下文中此类表述含义类似，不再重复说明。求解1(,)能够得到固定时拦截器能够到达的高度范围为∈[,]。

第二步为针对高度可达范围∈[,]，求解每个高度在飞行时长为时的平面可达范围，此时切换性能指标为拦截器飞行航程，记为

2(,,):

(5)

式中:为末端位置;为地球半径。

针对每一个高度求解2(,,)，即可得到每个高度对应的航程范围∈[,]，将末端位置转化为极坐标，即可得到飞行时长固定时拦截器能够到达的高度范围及不同高度的环形经纬度范围。

2.2 固定高度的上升轨迹可达范围

图2 固定高度拦截器可达范围Fig.2 Reachable domain of the interceptor at a fixed height

针对问题(,)，其末端飞行高度为定值。首先，需确定拦截器能够到达高度的飞行时长范围，也即以末端高度为约束，性能指标选取为飞行时长，记为

(6)

求解1(,)得到达到固定高度时拦截器的飞行时长范围为∈[,]。

第二步，针对飞行时长范围∈[,]，求解能够到达的环形平面经纬度范围。此问题中，无需再对进行划分，因为环形内外边界对应最小飞行时长的最短航程末端位置和最大飞行时长的最大航程末端位置，记为

2(,,):

(7)

求解2(,,)得到拦截器最大和最小航程对应的上升轨迹，进而通过上升轨迹末端位置极坐标转换确定固定高度的上升轨迹可达范围。

3 基于可达范围的发射窗口规划算法

发射窗口是指拦截器从地面起飞能够拦截到目标飞行器的起飞时刻集合。针对发射窗口计算问题，由于其是给定任务执行时间区间的关键依据，因此，发射窗口必须具备计算效率高、窗口表征参数具体等特点，为任务快速确定最佳的发射时间。同样在地心固连系下研究发射窗口的计算问题，对大气上升、大气层外空间拦截整个过程进行一体化设计，得到发射窗口。

在第2节的基础上，当目标轨迹与可拦截区域满足一定的位置关系时，目标可拦截，故对目标星下点与中每个时长对应的可达范围进行位置判断，可以得到针对目标拦截的发射窗口。

发射窗口计算的过程中，拦截器可达范围的计算与特定目标的相位信息无关，可以预先离线进行，只需在发现威胁目标时对目标实时星下点与预先得到的可拦截范围进行位置判定，即可快速得到针对特定目标的发射窗口。

为了清晰直观地说明发射窗口求解过程，此处以高度为圆轨道上的拦截器为目标，将三维空间中的可拦截性判定转换为固定高度的二维拦截判定，后续对椭圆轨道上目标拦截的发射窗口进行求解时，只需增加对不同高度拦截范围的判定即可。将发射窗口定义为

={|(,)∈(,)}

(8)

式中：(,)为时刻发射的拦截器在时刻到达目标高度的末端位置。(,)的求解过程在第2节已经给出。

对于低轨目标而言，拦截器到达此高度时对应的末端拦截区域包络一般不大。故先对所关注的时间段内发射窗口进行初筛，初步确定准发射窗口，可以大大减小精确窗口规划的计算量。

{[1,2]},∈{1,2,…,}

(9)

式中:1表示每次穿越时间区间的左边界;2表示每次穿越时间区间的右边界。

这个时间区间为星下点穿越最大可达范围的时间，最大飞行时长外边界的选取保证了初筛过程包含所有星下点穿越的情况。考虑到最大可达范围包含的区域半径从内到外对应的飞行时长不同，初筛过程应充分考虑不同飞行时长的影响，以保证精确发射窗口包含于准窗口中。根据式(6)得到的上升到目标高度的飞行时长范围∈[,]，可以求解得到初筛后的拦截器准发射窗口′为

(10)

式中

′=[1-,2-],∈{1,2,…,}

上述发射窗口初筛过程可以在后续精确发射窗口计算时极大程度地减少明显不属于发射窗口时间段的冗余计算，在保证发射窗口精度的基础上大大提高计算效率。

在窗口初筛的基础上计算精确发射窗口。目标星下点轨迹上每一点对应的时刻均不同，而可达范围半径由内到外对应的拦截器飞行时长也逐渐变化，所以需对飞行时长进行离散，针对每一离散点判断星下点与可达范围的关系，从而得到精确发射窗口。

根据任务窗口精度要求，将飞行时长区间[,]平均取+1个点，形成的飞行时长集合记为，则

=[,+,+2,…,+

(-1),]=[,,…,F(+1)]

(11)

式中：=(-)。

求解式(5)针对固定飞行时长可达范围计算问题2(,,)，可以得到目标高度处中每一飞行时长对应的环形可达范围，中所有元素对应的+1个可达范围组成的集合为

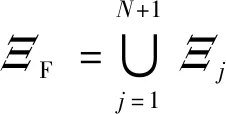
(12)

其中为飞行时长F对应的环形可达范围。

需要注意的是，对于拦截器飞行时长边界和，比更短和比更长飞行时长的拦截器均无法到达处，所以飞行时长为和对应的最小航程和最大航程上升轨迹重合，其可达范围为一条闭合曲线。图3给出了中部分元素的位置关系，其中≤。

图3 各可达范围子环位置关系Fig.3 Positional relationship of each reachable domain

中各可达范围子环与邻近子环可能存在交叉区域。由图3可以看出，目标星下点穿越最大可拦截范围的位置不同，所以星下点在准发射窗口′内不一定能够穿过每一个可达范围子环。

在初筛窗口的基础上进行精确发射窗口求解。如图3中目标星下点与各子环关系所示，对星下点轨迹加密，得到更靠近子环边界的星下点，进而保证发射窗口边界的准确性。以第一段准发射窗口为例，若在时间区间

[3,4]+F,=1,2,…,+1

(13)

内，目标星下点刚好位于可达子环中，则第一段准发射窗口对应的精确发射窗口为

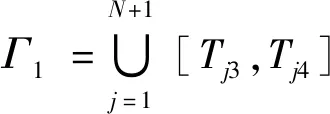
(14)

需要注意的是，考虑到星下点穿越最大范围的位置不同，上述+1个时间区间中，一部分可能为空集。如图3所示，目标星下点轨迹能够穿过的可达范围子环为,≥+1，此时，有且仅有[3,4]≠∅。

类似地，可以求得段准发射窗口对应的精确发射窗口，进而得到内精确发射窗口为

(15)

4 实例仿真与分析

针对特定目标拦截的过程中，一般整个飞行过程持续较短，故在窗口规划过程中忽略地球自转对上升过程的影响，且忽略目标拦截器受到的除中心引力外的各种摄动影响。选取拦截器为三级火箭，其各级参数如表1所示。

表1 三级拦截器参数Table 1 Three-stage interceptor parameters

4.1 固定飞行时长的上升轨迹可达范围

首先，针对不同高度处拦截器的可达范围进行研究。假设拦截器飞行时长固定，针对不同飞行时长的拦截器可达范围为固定时长可达范围的并集，所以此处以固定为例进行不同高度处可达范围计算说明。

在飞行时长固定的情况下，性能指标设置为末端飞行高度，即可得到拦截器在此飞行时长下能够到达的高度范围。针对不同高度处固定飞行时长对应的可达范围，切换性能指标为航程，进一步得到航程最大和航程最小分别对应的特定高度处拦截器可达最远和最近位置。图4给出了飞行时长为400 s和600 s时拦截器可达范围随高度的变化。

图4 特定飞行时长不同高度可达范围Fig.4 Reachable domain for given flight duration and different altitudes

4.2 固定目标高度的上升轨迹可达范围

考虑固定高度=2000 km的上升轨迹可达范围。首先，确定能够到达此高度的拦截器飞行时长范围，故以飞行时长为性能指标，末端高度为终端约束，通过求解式(6)，可以得到拦截器能够上升到2000 km高度的飞行时长范围为∈[5746,9554] s，时长跨度约380.8 s。

4.3 基于可达范围的发射窗口计算

考虑目标为=2000 km的圆轨道，对地面发射的拦截器能够对此目标进行拦截的发射窗口进行分析。目标轨道根数选取为：半长轴=8378 km，偏心率=0，轨道倾角=50°，升交点赤经=0°，近地点幅角=0°，真近点角=0°。

表2 发射窗口初筛结果Table 2 Screening results of launch windows

图5 目标星下点与可达范围位置关系Fig.5 The relation between the target sub-satellite points and the reachable domain

在得到准发射窗口′后，对拦截器飞行时长范围∈[5746,9554] s进行划分，此处将其离散为20段，得到飞行时长集合为

=[5746,5936,…,9364,9554] s=[,,……,]

针对中每一个飞行时长点，将性能指标切换为航程，进一步得到航程最大和航程最小分别对应的拦截器可达最远和最近位置，在0°～360°范围内遍历初始航向角，得到每个飞行时长对应的2000 km高度处可达环形区域=[,,…,]。

图6给出了最小时长、中间时长、最大时长对应的拦截器可达范围，可以看出，对于最大上升时长955.4 s和最小上升时长574.6 s，二者对应的拦截范围内外边界基本重合，这意味着拦截器轨迹末端无法到达最小上升时长对应圆环的更外侧或最大上升时长对应圆环的更内侧的位置，也验证了计算方法的正确性。

图6 不同飞行时长的拦截器环形可达范围Fig.6 Reachable domain for different flight durations

最后，在窗口初筛的基础上，考虑到实际飞行过程中受到的各种扰动和参数的不确定性，对目标星下点进行间隔为5 s的划分。对每一个上升时长对应的可达子环区域与目标航天器星下点位置关系进行判定，得到精确发射窗口如图7所示，其中，纵轴对应所划分的每一个飞行时长点，每段发射窗口对应的时刻如表3所示，每段准窗口中目标星下点能够穿越的中子环区域编号范围如表3中最后一列所示。

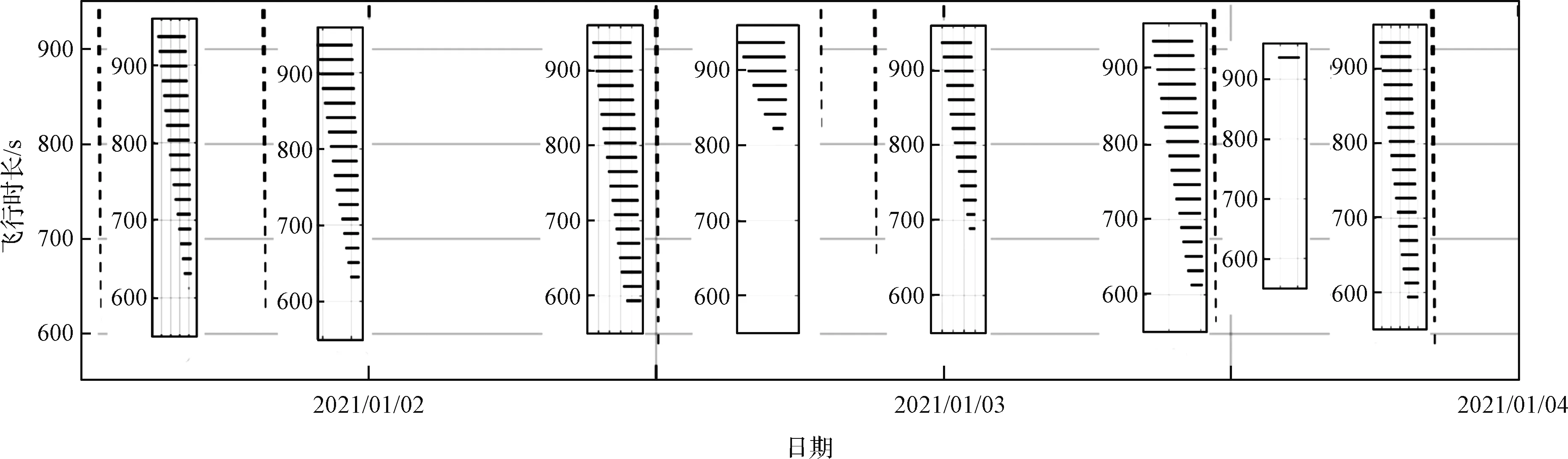
图7 2000 km高度目标精确发射窗口Fig.7 Accurate launch windows for targets at 2000 km altitude

由表3可以看出，8段精确发射窗口均位于8段准窗口中，验证了规划过程中窗口初筛过程的可靠性。由于拦截器星下点穿过可拦截区域的位置不同，3天内每一段发射窗口时长也有所差别。对于2000 km高度目标拦截器，3天内精确发射窗口时长共74分50秒。

4.4 计算效率分析

对本文提出的发射窗口计算方法的计算效率进行分析。根据工程需求，分两种情况进行分析：(1)任务前期的准发射窗口计算；(2)任务执行中精确发射窗口计算。

表3 2000 km高度目标发射窗口时刻Table 3 Launch windows for targets at 2000 km altitude

第一种情况对应4.3节前半部分准发射窗口计算过程，第二部分对应4.3节后半部分精确发射窗口计算过程，其中，特定高度拦截器各环形可达范围集合的计算只与目标飞行器的高度信息相关，所以在拦截器推进系统和物理参数确定之后随时可以进行计算，在任务即将执行时根据目标即时相位信息确定精确发射窗口。

在Intel i7-6700 CPU @3.40GHz处理器的MATLAB-R2018b计算环境下，针对2000 km高度目标拦截的发射窗口计算过程中，准发射窗口计算耗时16.8 s，精确发射窗口计算中，可达范围集合计算耗时181.2 s，精确窗口计算耗时0.92 s。

可以看到，在任务初期对窗口精度要求不高时，准窗口计算只需16.8 s左右，可以得到比精确发射窗口范围稍大的准窗口；精确窗口计算总时长需约3分钟，但可达范围计算部分可以预先根据发射位置和拦截器参数计算，并存储为数据库。针对不同高度和相位的具体目标，可达范围可通过查找数据库得到。在这种情况下，针对具体相位目标计算精确发射窗口计算时长为0.92 s。因此，针对特定情形，如拦截同轨道高度不同轨道面、不同相位的星座目标时，可快速得到针对每颗单星的精确发射窗口。

5 结 论

本文针对地面起飞的拦截器对低轨目标快速拦截的发射窗口规划问题，提出了基于上升轨迹可达范围分析的发射窗口初筛和精确求解算法。相对于传统方法，本文所提算法具有适用多种场景、计算准确简便的特点。本文研究可得到如下结论：

(1)所提基于上升轨迹可达范围的发射窗口初筛方法可快速给出准发射窗口，既提供了发射窗口的时间区间，也为后续精确窗口计算框定了范围。

(2)基于上升轨迹可达范围的发射窗口精确评估中，耗时较长的可达范围计算部分只根据目标的高度信息可离线进行。精确窗口计算根据目标相位信息在线实现，经过仿真，在普通个人计算机上，精确窗口计算时间仅需0.92 s。